Une introduction à la distribution de Rayleigh
La distribution de Rayleigh est une distribution de probabilité continue utilisée pour modéliser des variables aléatoires qui ne peuvent prendre que des valeurs égales ou supérieures à zéro.
Il a la fonction de densité de probabilité suivante :
f(x; σ) = (x/σ 2 )e -x 2 /(2σ 2 )
où σ est le paramètre d’échelle de la distribution.
Propriétés de la distribution de Rayleigh
La distribution de Rayleigh a les propriétés suivantes :
- Moyenne : σ√ π/2
- Écart : ((4-π)/2)σ 2
- Mode : σ
Puisque π a une valeur numérique connue, nous pouvons simplifier les propriétés comme suit :
- Moyenne : 1,253σ
- Écart : 0,429σ 2
- Mode : σ
Visualisation de la distribution de Rayleigh
Le graphique suivant montre la forme de la distribution de Rayleigh lorsqu’elle prend différentes valeurs pour le paramètre d’échelle :
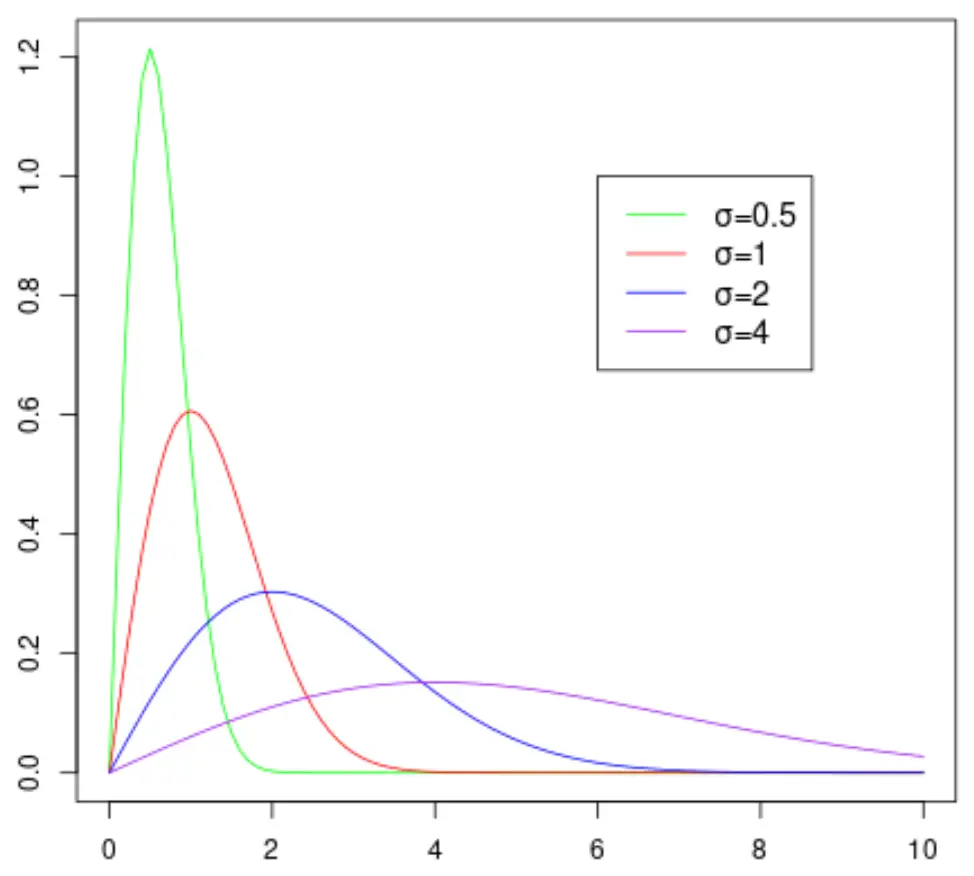
Notez que plus la valeur du paramètre d’échelle σ est grande, plus la distribution devient large.
Bonus : Pour ceux qui sont curieux, nous avons utilisé le code R suivant pour générer le graphique ci-dessus :
#load VGAM package library(VGAM) #create density plots curve(drayleigh(x, scale = 0.5), from=0, to=10, col='green') curve(drayleigh(x, scale = 1), from=0, to=10, col='red', add=TRUE) curve(drayleigh(x, scale = 2), from=0, to=10, col='blue', add=TRUE) curve(drayleigh(x, scale = 4), from=0, to=10, col='purple', add=TRUE) #add legend legend(6, 1, legend=c("σ=0.5", "σ=1", "σ=2", "σ=4"), col=c("green", "red", "blue", "purple"), lty=1, cex=1.2)
Relation avec d’autres distributions
La distribution de Rayleigh a la relation suivante avec d’autres distributions de probabilité :
1. Lorsque le paramètre d’échelle (σ) est égal à 1, la distribution de Rayleigh est égale à une distribution du Chi carré à 2 degrés de liberté.
2. La distribution de Rayleigh est un cas particulier de la distribution de Weibull avec un paramètre de forme k = 2.
3. La distribution de Rayleigh avec le paramètre d’échelle σ est égale à la distribution de Rice avec Rice(0, σ).
Applications
En pratique, la distribution Rayleigh est utilisée dans diverses applications, notamment :
1. La distribution de Rayleigh est utilisée pour modéliser le comportement des vagues dans l’océan, y compris le temps nécessaire aux vagues pour atteindre leur crête et la hauteur maximale atteinte par les vagues.
2. La distribution de Rayleigh est utilisée pour modéliser le comportement des données de fond en imagerie par résonance magnétique, plus communément appelée IRM.
3. La distribution de Rayleigh est utilisée dans le domaine de la nutrition pour modéliser la relation entre les niveaux de nutriments et la réponse nutritionnelle chez les humains et les animaux.
Ressources additionnelles
Les didacticiels suivants fournissent des informations supplémentaires sur d’autres distributions dans les statistiques :
Une introduction à la distribution normale
Une introduction à la distribution binomiale
Une introduction à la distribution de Poisson
