Comment tracer plusieurs résultats de régression linéaire dans R

Lorsque nous effectuons une régression linéaire simple dans R, il est facile de visualiser la droite de régression ajustée car nous travaillons uniquement avec une seule variable prédictive et une seule variable de réponse .

Par exemple, le code suivant montre comment ajuster un modèle de régression linéaire simple à un ensemble de données et tracer les résultats :

#create dataset
data <- data.frame(x = c(1, 1, 2, 4, 4, 5, 6, 7, 7, 8, 9, 10, 11, 11),
                   y = c(13, 14, 17, 23, 24, 25, 25, 24, 28, 32, 33, 35, 40, 41))

#fit simple linear regression model
model <- lm(y ~ x, data = data)

#create scatterplot of data
plot(data$x, data$y)

#add fitted regression line
abline(model)

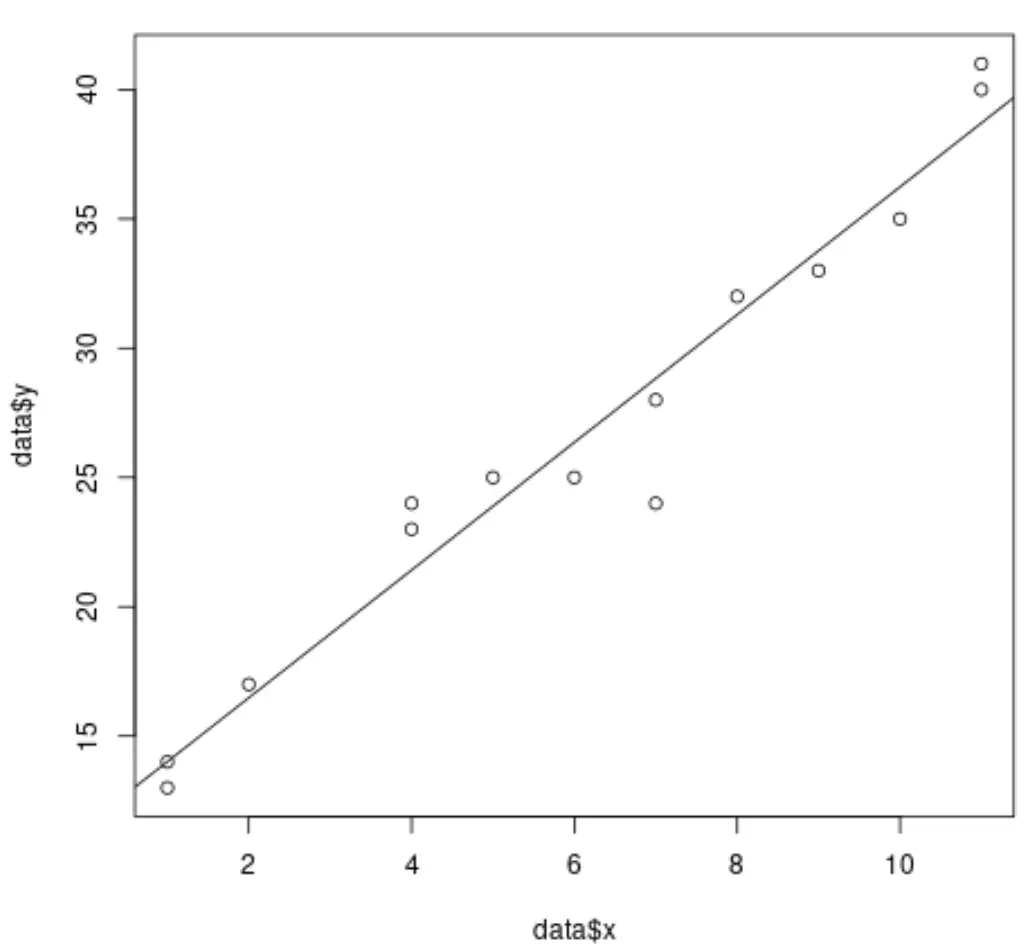
Cependant, lorsque nous effectuons une régression linéaire multiple, il devient difficile de visualiser les résultats car il existe plusieurs variables prédictives et nous ne pouvons pas simplement tracer une droite de régression sur un graphique 2D.

Au lieu de cela, nous pouvons utiliser des tracés de variables ajoutées (parfois appelés « tracés de régression partielle »), qui sont des tracés individuels qui affichent la relation entre la variable de réponse et une variable prédictive, tout en contrôlant la présence d’autres variables prédictives dans le modèle .

L’exemple suivant montre comment effectuer une régression linéaire multiple dans R et visualiser les résultats à l’aide de tracés de variables ajoutés.

Exemple : traçage des résultats de régression linéaire multiple dans R

Supposons que nous adaptions le modèle de régression linéaire multiple suivant à un ensemble de données dans R à l’aide de l’ensemble de données mtcars intégré :

#fit multiple linear regression model
model <- lm(mpg ~ disp + hp + drat, data = mtcars)

#view results of model
summary(model)

Call:
lm(formula = mpg ~ disp + hp + drat, data = mtcars)

Residuals:
    Min      1Q  Median      3Q     Max 
-5.1225 -1.8454 -0.4456  1.1342  6.4958 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept) 19.344293   6.370882   3.036  0.00513 **
disp        -0.019232   0.009371  -2.052  0.04960 * 
hp          -0.031229   0.013345  -2.340  0.02663 * 
drat         2.714975   1.487366   1.825  0.07863 . 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.008 on 28 degrees of freedom
Multiple R-squared:  0.775,	Adjusted R-squared:  0.7509 
F-statistic: 32.15 on 3 and 28 DF,  p-value: 3.28e-09

D’après les résultats, nous pouvons voir que la valeur p pour chacun des coefficients est inférieure à 0,1. Par souci de simplicité, nous supposerons que chacune des variables prédictives est significative et doit être incluse dans le modèle.

Pour produire des tracés de variables ajoutés, nous pouvons utiliser la fonction avPlots() du package car :

#load car package
library(car)

#produce added variable plots
avPlots(model)

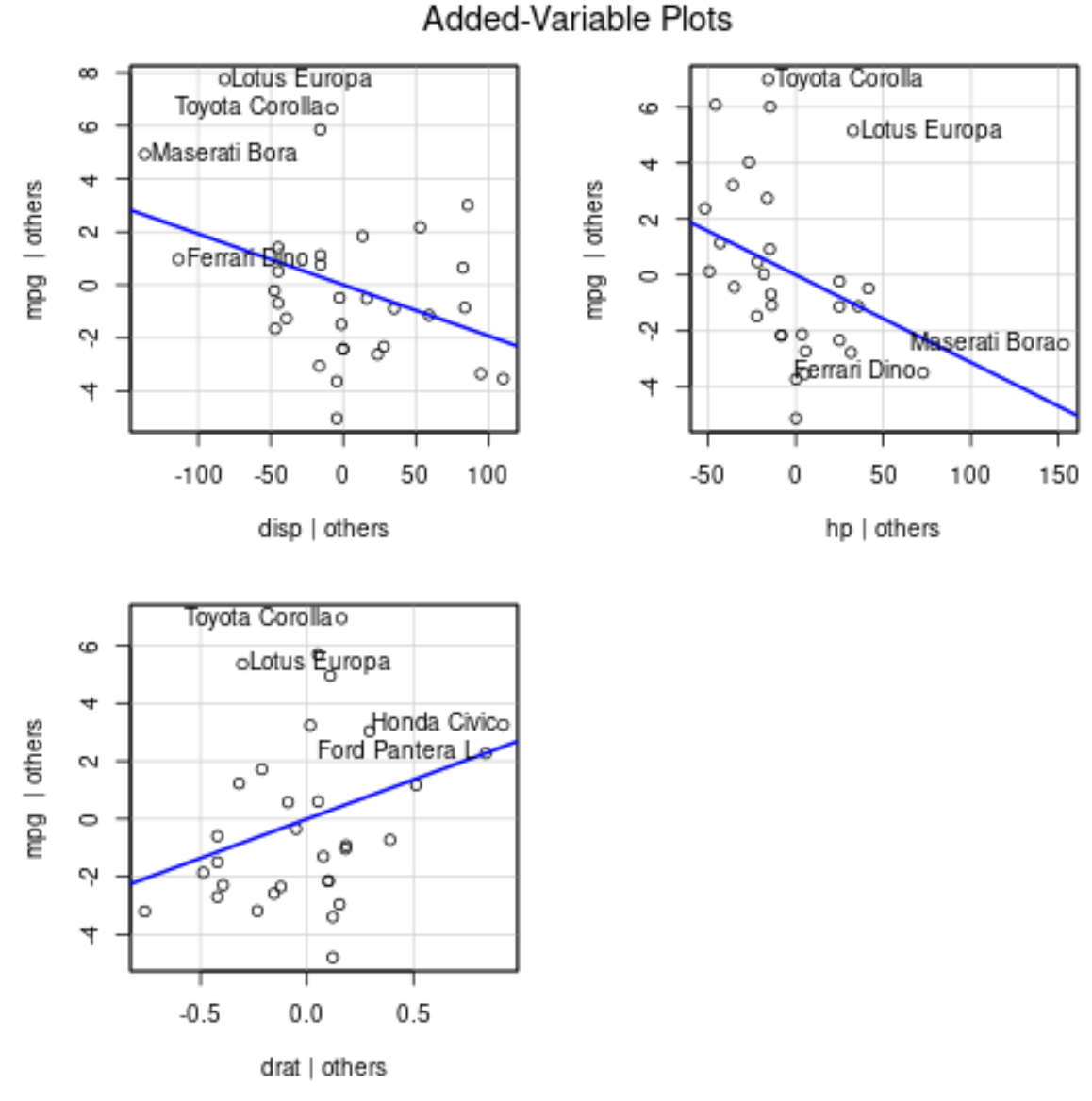
Voici comment interpréter chaque intrigue :

• L’axe des x affiche une seule variable prédictive et l’axe des y affiche la variable de réponse.
• La ligne bleue montre l’association entre la variable prédictive et la variable de réponse, tout en maintenant constante la valeur de toutes les autres variables prédictives .
• Les points étiquetés dans chaque graphique représentent les 2 observations avec les résidus les plus importants et les 2 observations avec le levier partiel le plus important.

Notez que l’angle de la ligne dans chaque tracé correspond au signe du coefficient de l’équation de régression estimée.

Par exemple, voici les coefficients estimés pour chaque variable prédictive du modèle :

• affichage : -0,019232
• ch : -0,031229
• date : 2.714975

Notez que l’angle de la ligne est positif dans le tracé des variables ajoutées pour drat tandis qu’il est négatif pour disp et hp , ce qui correspond aux signes de leurs coefficients estimés :

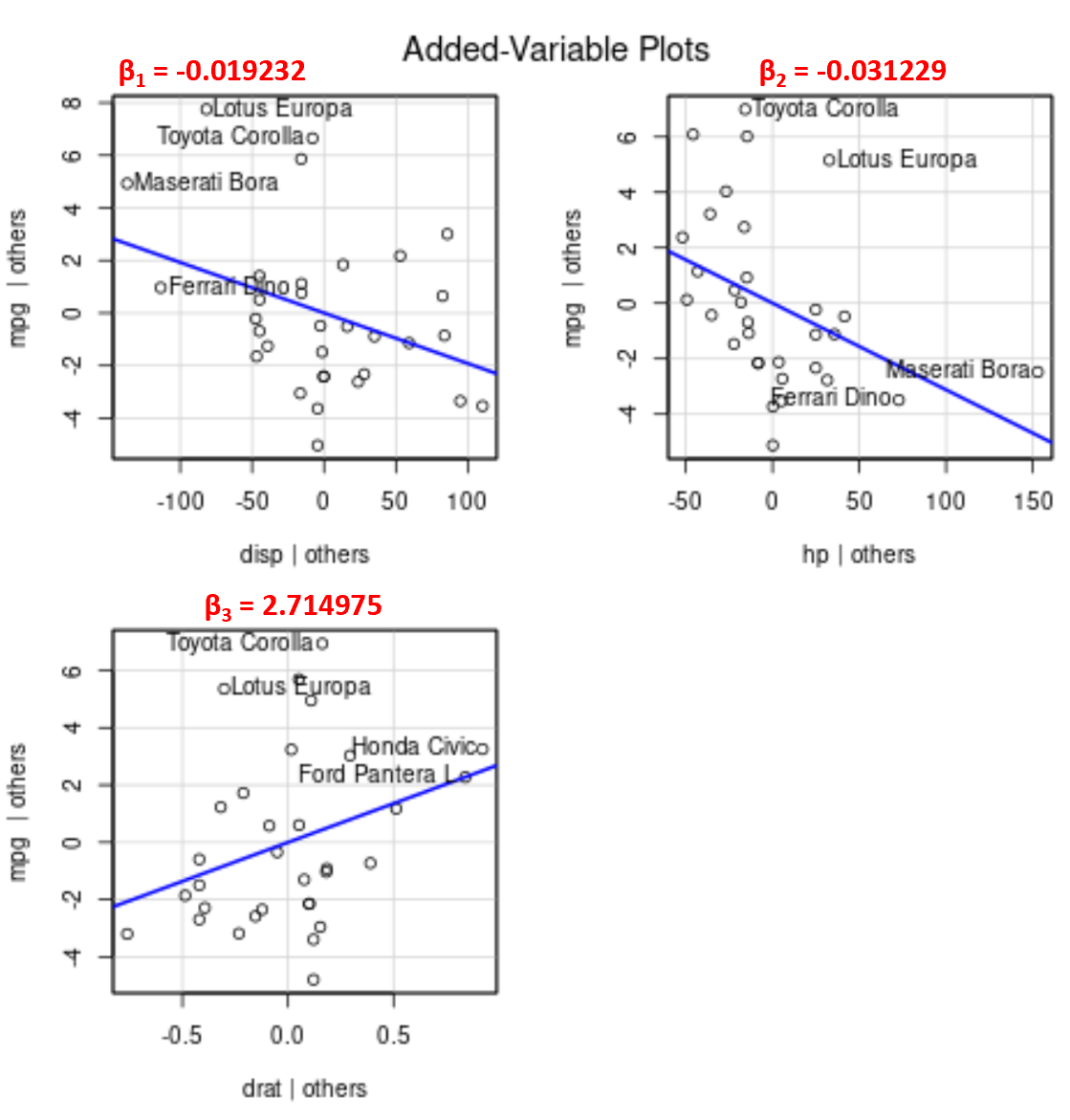
Bien que nous ne puissions pas tracer une seule ligne de régression ajustée sur un graphique 2D puisque nous avons plusieurs variables prédictives, ces graphiques de variables ajoutées nous permettent d’observer la relation entre chaque variable prédictive individuelle et la variable de réponse tout en maintenant constantes les autres variables prédictives.