Comment calculer un coefficient Phi dans R

Un coefficient Phi (parfois appelé coefficient de contingence quadratique moyen ) est une mesure de l’association entre deux variables binaires.

Pour un tableau 2×2 donné pour deux variables aléatoires x et y :

Le coefficient Phi peut être calculé comme suit :

Φ = (AD-BC) / √ (A+B)(C+D)(A+C)(B+D)

Exemple : Calcul d’un coefficient Phi dans R

Supposons que nous voulions savoir si le sexe est associé ou non à la préférence pour un parti politique. Nous prenons donc un échantillon aléatoire simple de 25 électeurs et les interrogeons sur leur préférence pour un parti politique.

Le tableau suivant présente les résultats de l’enquête :

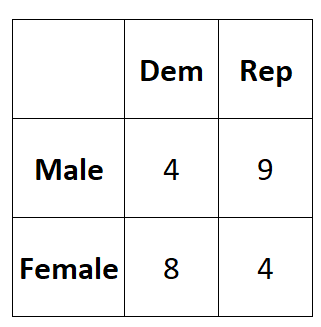
Nous pouvons utiliser le code suivant pour saisir ces données dans une matrice 2×2 dans R :

#create 2x2 table
data = matrix(c(4, 8, 9, 4), nrow = 2)

#view dataset
data

     [,1] [,2]
[1,]    4    9
[2,]    8    4

Nous pouvons ensuite utiliser la fonction phi() du package psych pour calculer le coefficient Phi entre les deux variables :

#load psych package
library(psych)

#calculate Phi Coefficient
phi(data)

[1] -0.36

Le coefficient Phi s’avère être de -0,36 .

Notez que la fonction phi arrondit à 2 chiffres par défaut, mais vous pouvez spécifier la fonction pour arrondir à autant de chiffres que vous le souhaitez :

#calculate Phi Coefficient and round to 6 digits
phi(data, digits = 6)

[1] -0.358974

Comment interpréter un coefficient Phi

Semblable à un coefficient de corrélation de Pearson, un coefficient Phi prend des valeurs comprises entre -1 et 1 où :

• -1 indique une relation parfaitement négative entre les deux variables.
• 0 indique aucune association entre les deux variables.
• 1 indique une relation parfaitement positive entre les deux variables.

En général, plus un coefficient Phi est éloigné de zéro, plus la relation entre les deux variables est forte.

En d’autres termes, plus un coefficient Phi est éloigné de zéro, plus il y a de preuves d’un certain type de modèle systématique entre les deux variables.

Ressources additionnelles

Une introduction au coefficient Phi
Calculateur du coefficient Phi