Qu’est-ce que Somers’ D? (Définition & #038; Exemple)

Somers’ D , abréviation de Somers’ Delta, est une mesure de la force et de la direction de l’association entre une variable dépendante ordinale et une variable indépendante ordinale.

Une variable ordinale est une variable dans laquelle les valeurs ont un ordre naturel (par exemple « mauvais », « neutre », « bon »).

La valeur du D de Somers est comprise entre -1 et 1 où :

• -1 : Indique que toutes les paires de variables ne sont pas d’accord
• 1 : indique que toutes les paires de variables concordent

Somers’ D est utilisé en pratique pour de nombreuses méthodes statistiques non paramétriques.

Somers’ D : définition

Étant donné deux variables, X et Y, on peut dire :

• Deux paires (x _i , y _i ) et (x _j , y _j ) sont concordantes si les rangs des deux éléments concordent.
• Deux paires (x _i , y _i ) et (x _j , y _j ) sont discordantes si les rangs des deux éléments concordent.

On peut alors calculer le D de Somers en utilisant la formule suivante :

Somers’ D = (N _C – N _D ) / (N _C + N _D + N _T )

où:

• N _C : Le nombre de paires concordantes
• N _D : Le nombre de paires discordantes
• N _T : Le nombre de paires ex aequo

La valeur résultante sera toujours comprise entre -1 et 1.

Somers’ D : exemple en R

Supposons qu’une épicerie souhaite évaluer la relation entre les deux variables ordinales suivantes :

• La gentillesse globale du caissier (classée de 1 à 3)
• La satisfaction globale de l’expérience client (également classée de 1 à 3)

Ils collectent les notes suivantes auprès d’un échantillon de 10 clients :

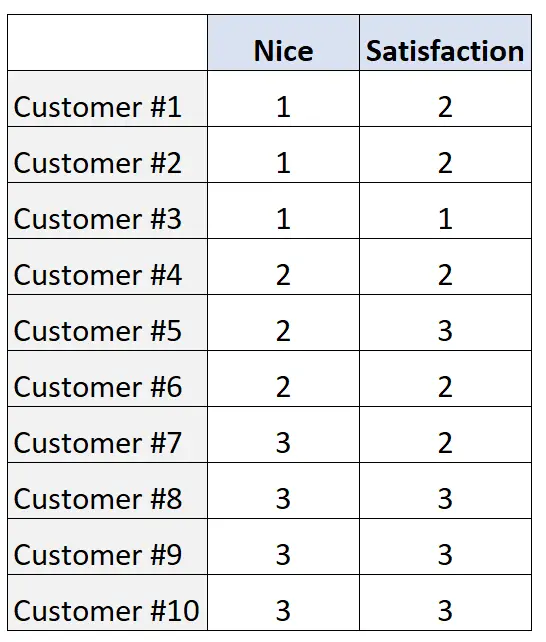
Pour quantifier la relation entre les deux variables, nous pouvons calculer le D de Somers en utilisant le code suivant dans R :

#enter data
nice <- c(1, 1, 1, 2, 2, 2, 3, 3, 3, 3)
satisfaction <- c(2, 2, 1, 2, 3, 2, 2, 3, 3, 3)

#load DescTools package
library(DescTools)

#calculate Somers' D
SomersDelta(nice, satisfaction)

[1] 0.6896552

Le D de Somers s’avère être 0,6896552 .

Cette valeur étant assez proche de 1, cela indique qu’il existe une relation positive assez forte entre les deux variables.

Cela est intuitivement logique : les clients qui jugent les caissiers plus gentils ont également tendance à évaluer leur satisfaction globale plus élevée.

Ressources additionnelles

Une introduction au coefficient de corrélation de Pearson
Une introduction au Tau de Kendall