Comment calculer DFBETAS dans R

En statistiques, nous souhaitons souvent savoir quelle est l’influence des différentes observations dans les modèles de régression.

Une façon de calculer l’influence des observations consiste à utiliser une métrique connue sous le nom de DFBETAS , qui nous indique l’effet standardisé sur chaque coefficient de la suppression de chaque observation individuelle.

Cette métrique nous donne une idée de l’influence de chaque observation sur chaque estimation de coefficient dans un modèle de régression donné.

Ce didacticiel montre un exemple étape par étape de la façon de calculer et de visualiser DFBETAS pour chaque observation dans un modèle dans R.

Étape 1 : Créer un modèle de régression

Tout d’abord, nous allons créer un modèle de régression linéaire multiple à l’aide de l’ensemble de données mtcars intégré dans R :

#fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904   1.331566  23.083  < 2e-16 ***
disp        -0.030346   0.007405  -4.098 0.000306 ***
hp          -0.024840   0.013385  -1.856 0.073679 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared:  0.7482,	Adjusted R-squared:  0.7309 
F-statistic: 43.09 on 2 and 29 DF,  p-value: 2.062e-09

Étape 2 : Calculer DFBETAS pour chaque observation

Ensuite, nous utiliserons la fonction intégrée dfbetas() pour calculer les valeurs DFBETAS pour chaque observation du modèle :

#calculate DFBETAS for each observation in the model
dfbetas <- as.data.frame(dfbetas(model))

#display DFBETAS for each observation
dfbetas

                      (Intercept)         disp            hp
Mazda RX4           -0.1174171253  0.030760632  1.748143e-02
Mazda RX4 Wag       -0.1174171253  0.030760632  1.748143e-02
Datsun 710          -0.1694989349  0.086630144 -3.332781e-05
Hornet 4 Drive       0.0577309674  0.078971334 -8.705488e-02
Hornet Sportabout   -0.0204333878  0.237526523 -1.366155e-01
Valiant             -0.1711908285 -0.139135639  1.829038e-01
Duster 360          -0.0312338677 -0.005356209  3.581378e-02
Merc 240D           -0.0312259577 -0.010409922  2.433256e-02
Merc 230            -0.0865872595  0.016428917  2.287867e-02
Merc 280            -0.1560683502  0.078667906 -1.911180e-02
Merc 280C           -0.2254489597  0.113639937 -2.760800e-02
Merc 450SE           0.0022844093  0.002966155 -2.855985e-02
Merc 450SL           0.0009062022  0.001176644 -1.132941e-02
Merc 450SLC          0.0041566755  0.005397169 -5.196706e-02
Cadillac Fleetwood   0.0388832216 -0.134511133  7.277283e-02
Lincoln Continental  0.0483781688 -0.121146607  5.326220e-02
Chrysler Imperial   -0.1645266331  0.236634429 -3.917771e-02
Fiat 128             0.5720358325 -0.181104179 -1.265475e-01
Honda Civic          0.3490872162 -0.053660545 -1.326422e-01
Toyota Corolla       0.7367058819 -0.268512348 -1.342384e-01
Toyota Corona       -0.2181110386  0.101336902  5.945352e-03
Dodge Challenger    -0.0270169005 -0.123610713  9.441241e-02
AMC Javelin         -0.0406785103 -0.141711468  1.074514e-01
Camaro Z28           0.0390139262  0.012846225 -5.031588e-02
Pontiac Firebird    -0.0549059340  0.574544346 -3.689584e-01
Fiat X1-9            0.0565157245 -0.017751582 -1.262221e-02
Porsche 914-2        0.0839169111 -0.028670987 -1.240452e-02
Lotus Europa         0.3444562478 -0.402678927  2.135224e-01
Ford Pantera L      -0.1598854695 -0.094184733  2.320845e-01
Ferrari Dino        -0.0343997122  0.248642444 -2.344154e-01
Maserati Bora       -0.3436265545 -0.511285637  7.319066e-01
Volvo 142E          -0.1784974091  0.132692956 -4.433915e-02

Pour chaque observation, nous pouvons voir la différence dans l’estimation du coefficient pour l’origine, la variable disp et la variable hp qui se produit lorsque nous supprimons cette observation particulière.

Généralement, nous considérons qu’une observation a une forte influence sur l’estimation d’un coefficient donné si elle a une valeur DBETAS supérieure à un seuil de 2/√ n où n est le nombre d’observations.

Dans cet exemple, le seuil serait 0,3535534 :

#find number of observations
n <- nrow(mtcars)

#calculate DFBETAS threshold value
thresh <- 2/sqrt(n)

thresh

[1] 0.3535534

Étape 3 : Visualisez le DFBETAS

Enfin, nous pouvons créer des tracés pour visualiser la valeur DFBETAS pour chaque observation et pour chaque prédicteur du modèle :

#specify 2 rows and 1 column in plotting region
par(mfrow=c(2,1))

#plot DFBETAS for disp with threshold lines
plot(dfbetas$disp, type='h')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

#plot DFBETAS for hp with threshold lines 
plot(dfbetas$hp, type='h')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

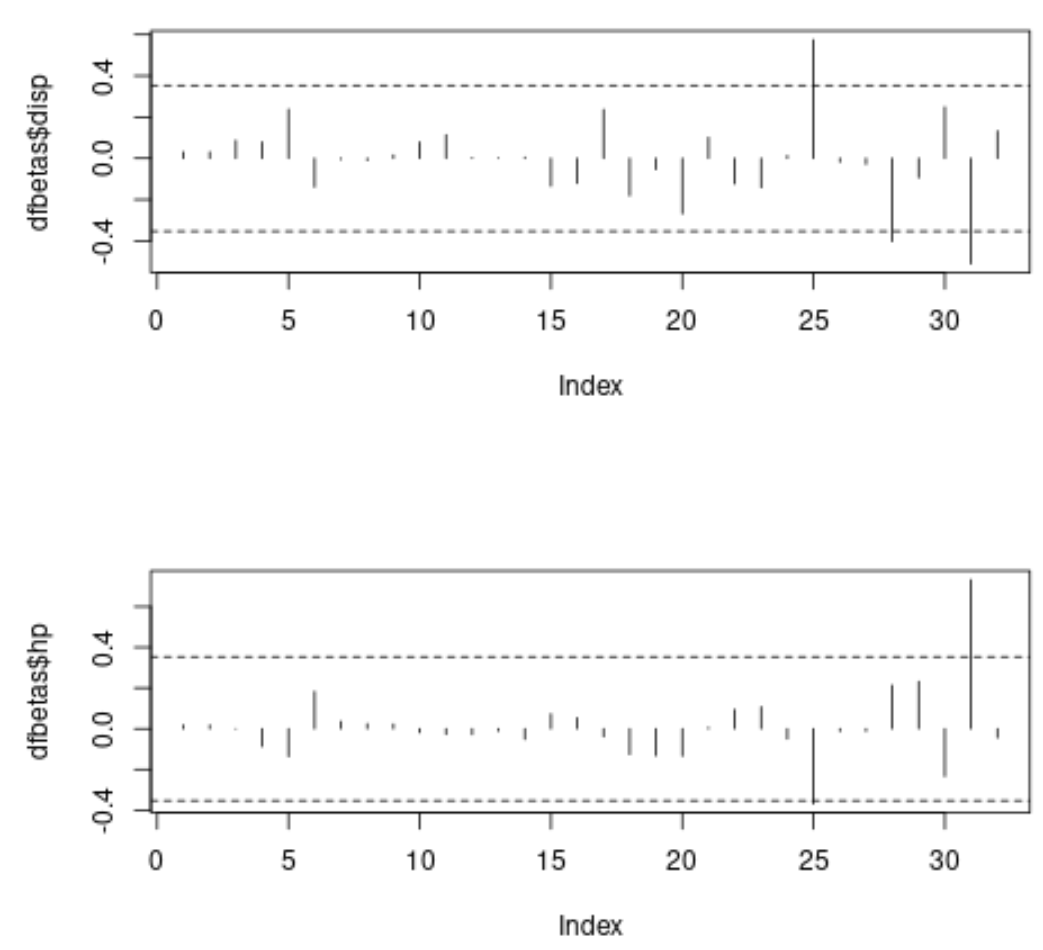
Dans chaque tracé, l’axe des x affiche l’indice de chaque observation dans l’ensemble de données et la valeur y affiche le DFBETAS correspondant pour chaque observation et chaque prédicteur.

Sur le premier tracé, nous pouvons voir que trois observations dépassent la valeur absolue du seuil de 0,3535534 et sur le deuxième tracé, nous pouvons voir que deux observations dépassent la valeur absolue du seuil.

Nous pouvons choisir d’étudier ces observations de plus près pour déterminer si elles ont une influence excessive sur l’estimation des coefficients du modèle.

Ressources additionnelles

Comment effectuer une régression linéaire simple dans R
Comment effectuer une régression linéaire multiple dans R
Comment calculer les statistiques de levier dans R
Comment calculer les DFFITS dans R