Comment calculer les résidus studentisés en Python

Un résidu étudiant est simplement un résidu divisé par son écart type estimé.

En pratique, nous disons généralement que toute observation dans un ensemble de données dont le résidu étudiant est supérieur à une valeur absolue de 3 est une valeur aberrante.

On peut obtenir rapidement les résidus studentisés d’un modèle de régression en Python en utilisant la fonction OLSResults.outlier_test() de statsmodels, qui utilise la syntaxe suivante :

OLSResults.outlier_test()

où OLSResults est le nom d’un ajustement de modèle linéaire à l’aide de la fonction ols() de statsmodels.

Exemple : calcul des résidus studentisés en Python

Supposons que nous construisions le modèle de régression linéaire simple suivant en Python :

#import necessary packages and functions
import numpy as np
import pandas as pd
import statsmodels.api as sm
from statsmodels.formula.api import ols

#create dataset
df = pd.DataFrame({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86],
                   'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19]})

#fit simple linear regression model
model = ols('rating ~ points', data=df).fit()

Nous pouvons utiliser la fonction outlier_test() pour produire un DataFrame qui contient les résidus studentisés pour chaque observation de l’ensemble de données :

#calculate studentized residuals
stud_res = model.outlier_test()

#display studentized residuals
print(stud_res)

    student_resid	 unadj_p	 bonf(p)
0	-0.486471	0.641494	1.000000
1	-0.491937	0.637814	1.000000
2 	 0.172006	0.868300	1.000000
3	 1.287711	0.238781	1.000000
4	 0.106923	0.917850	1.000000
5	 0.748842	0.478355	1.000000
6	-0.968124	0.365234	1.000000
7	-2.409911	0.046780	0.467801
8	 1.688046	0.135258	1.000000
9	-0.014163	0.989095	1.000000

Ce DataFrame affiche les valeurs suivantes pour chaque observation de l’ensemble de données :

• Le résidu studentisé
• La valeur p non ajustée du résidu studentisé
• La valeur p corrigée par Bonferroni du résidu étudiant

Nous pouvons voir que le résidu studentisé pour la première observation de l’ensemble de données est -0,486471 , le résidu studentisé pour la deuxième observation est -0,491937 , et ainsi de suite.

Nous pouvons également créer un tracé rapide des valeurs des variables prédictives par rapport aux résidus studentisés correspondants :

import matplotlib.pyplot as plt

#define predictor variable values and studentized residuals
x = df['points']
y = stud_res['student_resid']

#create scatterplot of predictor variable vs. studentized residuals
plt.scatter(x, y)
plt.axhline(y=0, color='black', linestyle='--')
plt.xlabel('Points')
plt.ylabel('Studentized Residuals') 

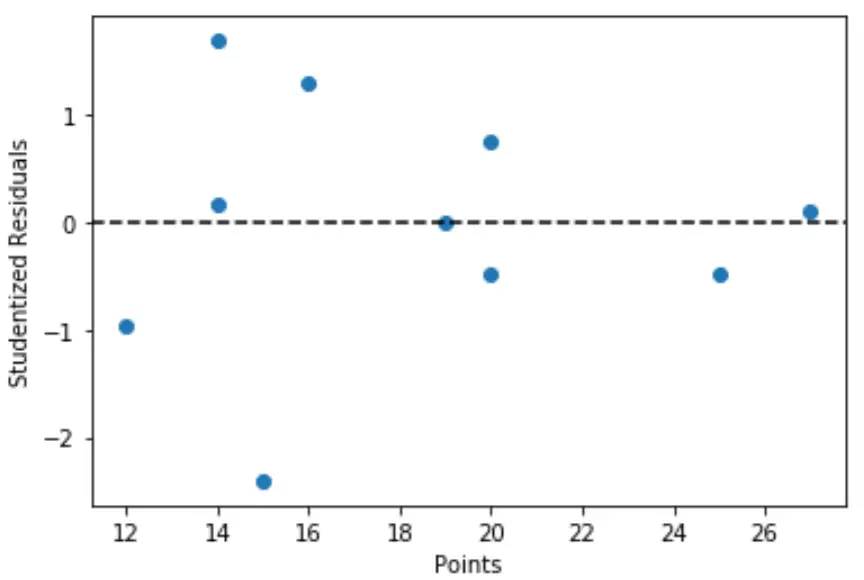
D’après le graphique, nous pouvons voir qu’aucune des observations n’a de résidu étudiant avec une valeur absolue supérieure à 3, il n’y a donc pas de valeurs aberrantes claires dans l’ensemble de données.

Ressources additionnelles

Comment effectuer une régression linéaire simple en Python
Comment effectuer une régression linéaire multiple en Python
Comment créer un tracé résiduel en Python