K-Medoids dans R : exemple étape par étape

Le clustering est une technique d’apprentissage automatique qui tente de trouver des groupes ou des grappes d’ observations au sein d’un ensemble de données.

L’objectif est de trouver des clusters tels que les observations au sein de chaque cluster soient assez similaires les unes aux autres, tandis que les observations dans différents clusters sont assez différentes les unes des autres.

Le clustering est une forme d’ apprentissage non supervisé car nous essayons simplement de trouver une structure au sein d’un ensemble de données plutôt que de prédire la valeur d’une variable de réponse .

Le clustering est souvent utilisé en marketing lorsque les entreprises ont accès à des informations telles que :

• Revenu du ménage
• La taille du ménage
• Chef de famille Profession
• Distance de la zone urbaine la plus proche

Lorsque ces informations sont disponibles, le regroupement peut être utilisé pour identifier les ménages similaires et susceptibles d’être plus susceptibles d’acheter certains produits ou de mieux répondre à un certain type de publicité.

L’une des formes de clustering les plus courantes est connue sous le nom de clustering k-means .

Malheureusement, cette méthode peut être influencée par des valeurs aberrantes, c’est pourquoi une alternative souvent utilisée est le clustering k-médoïdes .

Qu’est-ce que le clustering K-Medoids ?

Le clustering K-médoïdes est une technique dans laquelle nous plaçons chaque observation d’un ensemble de données dans l’un des K clusters.

L’objectif final est d’avoir K clusters dans lesquels les observations au sein de chaque cluster sont assez similaires les unes aux autres tandis que les observations dans différents clusters sont assez différentes les unes des autres.

En pratique, nous utilisons les étapes suivantes pour effectuer un clustering K-means :

1. Choisissez une valeur pour K .

• Tout d’abord, nous devons décider combien de clusters nous souhaitons identifier dans les données. Souvent, nous devons simplement tester plusieurs valeurs différentes pour K et analyser les résultats pour voir quel nombre de clusters semble avoir le plus de sens pour un problème donné.

2. Attribuez aléatoirement chaque observation à un cluster initial, de 1 à K.

3. Effectuez la procédure suivante jusqu’à ce que les affectations de cluster cessent de changer.

• Pour chacun des K clusters, calculez le centre de gravité du cluster. Il s’agit du vecteur des p médianes des caractéristiques pour les observations du k ème cluster.
• Attribuez chaque observation au cluster dont le centre de gravité est le plus proche. Ici, le plus proche est défini en utilisant la distance euclidienne .

Note technique :

Étant donné que k-medoids calcule les centroïdes de cluster en utilisant les médianes plutôt que les moyennes, il a tendance à être plus robuste aux valeurs aberrantes que les k-means.

En pratique, s’il n’y a pas de valeurs aberrantes extrêmes dans l’ensemble de données, les k-moyennes et les k-médoïdes produiront des résultats similaires.

Clustering K-Medoids dans R

Le didacticiel suivant fournit un exemple étape par étape de la façon d’effectuer un clustering k-médoïdes dans R.

Étape 1 : Chargez les packages nécessaires

Tout d’abord, nous allons charger deux packages contenant plusieurs fonctions utiles pour le clustering k-medoids dans R.

library(factoextra)
library(cluster)

Étape 2 : charger et préparer les données

Pour cet exemple, nous utiliserons l’ensemble de données USArrests intégré à R, qui contient le nombre d’arrestations pour 100 000 habitants dans chaque État américain en 1973 pour meurtre , agression et viol , ainsi que le pourcentage de la population de chaque État vivant dans des zones urbaines. , UrbanPop .

Le code suivant montre comment effectuer les opérations suivantes :

• Charger l’ensemble de données USArrests
• Supprimez toutes les lignes avec des valeurs manquantes
• Mettez à l’échelle chaque variable de l’ensemble de données pour avoir une moyenne de 0 et un écart type de 1

#load data
df <- USArrests

#remove rows with missing values
df <- na.omit(df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder   Assault   UrbanPop         Rape
Alabama    1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska     0.50786248 1.1068225 -1.2117642  2.484202941
Arizona    0.07163341 1.4788032  0.9989801  1.042878388
Arkansas   0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144  1.7589234  2.067820292
Colorado   0.02571456 0.3988593  0.8608085  1.864967207

Étape 3 : Trouver le nombre optimal de clusters

Pour effectuer un clustering k-médoïdes dans R, nous pouvons utiliser la fonction pam() , qui signifie « partitionnement autour des médianes » et utilise la syntaxe suivante :

pam(data, k, metric = « euclidien », stand = FALSE)

où:

• data : Nom de l’ensemble de données.
• k : Le nombre de clusters.
• métrique : la métrique à utiliser pour calculer la distance. La valeur par défaut est euclidienne mais vous pouvez également spécifier manhattan .
• stand : s’il faut ou non normaliser chaque variable de l’ensemble de données. La valeur par défaut est FALSE.

Puisque nous ne savons pas à l’avance quel nombre de clusters est optimal, nous allons créer deux graphiques différents qui peuvent nous aider à décider :

1. Nombre de clusters par rapport au total dans la somme des carrés

Tout d’abord, nous utiliserons la fonction fviz_nbclust() pour créer un tracé du nombre de clusters par rapport au total dans la somme des carrés :

fviz_nbclust(df, pam, method = "wss")

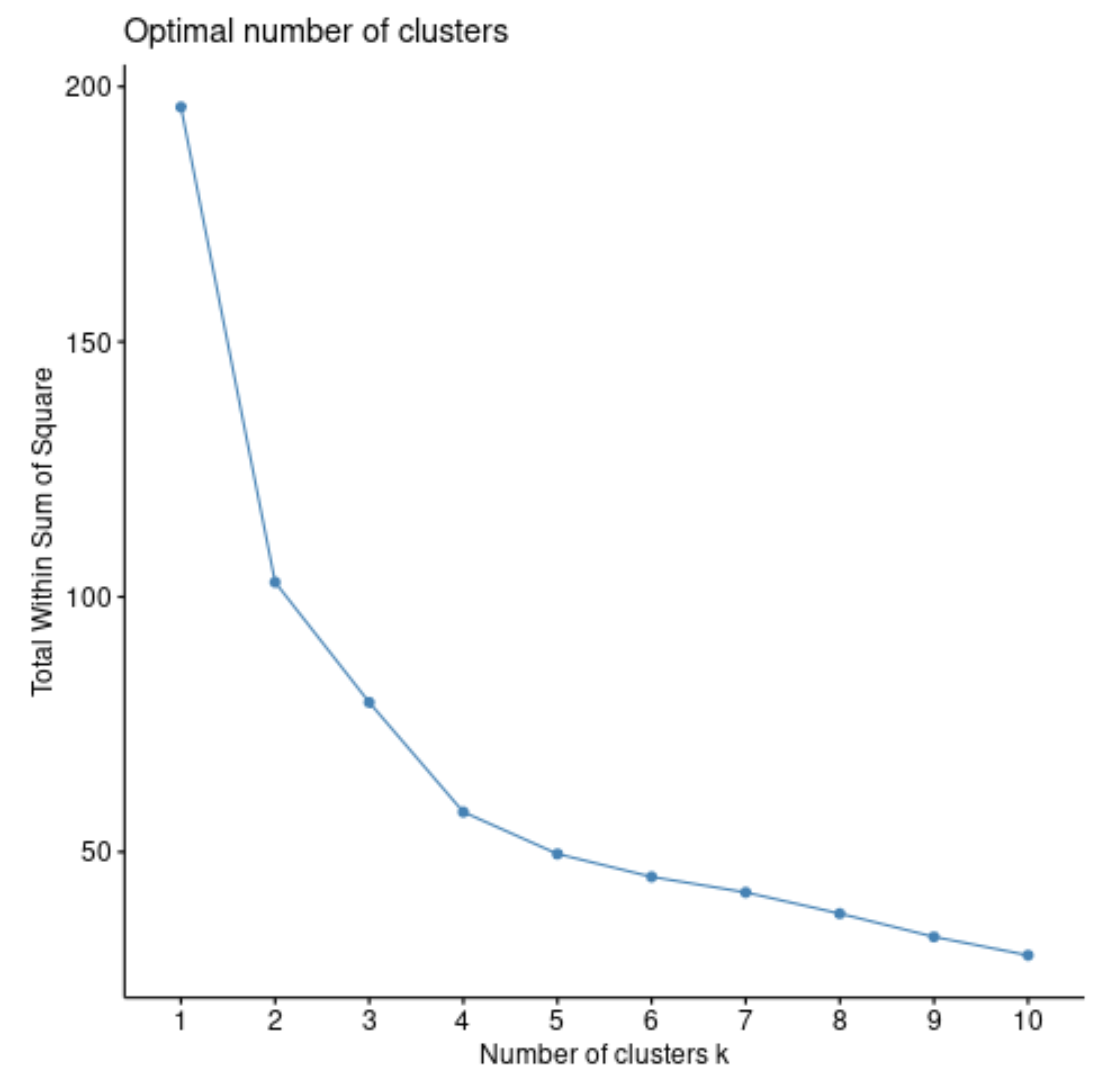
Le total dans la somme des carrés augmentera généralement toujours à mesure que nous augmentons le nombre de grappes. Ainsi, lorsque nous créons ce type de tracé, nous recherchons un « coude » où la somme des carrés commence à « se plier » ou à se stabiliser.

Le point de courbure du tracé correspond généralement au nombre optimal de clusters. Au-delà de ce chiffre, un surapprentissage est susceptible de se produire.

Pour ce graphique, il semble qu’il y ait un petit coude ou « courbure » à k = 4 clusters.

2. Nombre de clusters par rapport aux statistiques d’écart

Une autre façon de déterminer le nombre optimal de clusters consiste à utiliser une métrique appelée statistique d’écart , qui compare la variation totale intra-cluster pour différentes valeurs de k avec leurs valeurs attendues pour une distribution sans clustering.

Nous pouvons calculer la statistique d’écart pour chaque nombre de clusters à l’aide de la fonction clusGap() du package cluster ainsi qu’un graphique des clusters par rapport aux statistiques d’écart à l’aide de la fonction fviz_gap_stat() :

#calculate gap statistic based on number of clusters
gap_stat <- clusGap(df,
                    FUN = pam,
                    K.max = 10, #max clusters to consider
                    B = 50) #total bootstrapped iterations

#plot number of clusters vs. gap statistic
fviz_gap_stat(gap_stat)

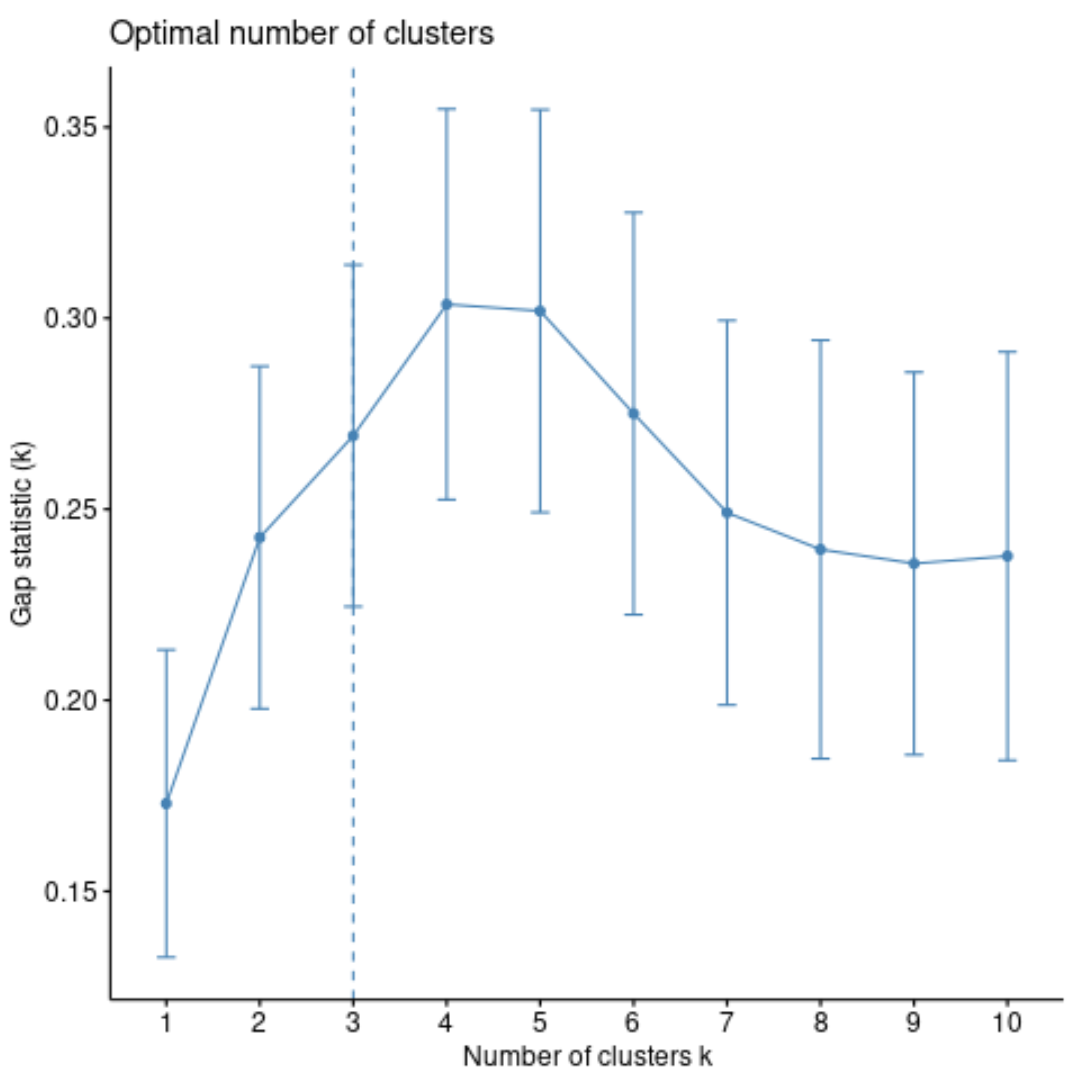
À partir du graphique, nous pouvons voir que la statistique d’écart est la plus élevée à k = 4 clusters, ce qui correspond à la méthode du coude que nous avons utilisée précédemment.

Étape 4 : Effectuer le clustering K-Medoids avec Optimal K

Enfin, nous pouvons effectuer un clustering k-médoïdes sur l’ensemble de données en utilisant la valeur optimale pour k de 4 :

#make this example reproducible
set.seed(1)

#perform k-medoids clustering with k = 4 clusters
kmed <- pam(df, k = 4)

#view results
kmed

              ID     Murder    Assault   UrbanPop         Rape
Alabama        1  1.2425641  0.7828393 -0.5209066 -0.003416473
Michigan      22  0.9900104  1.0108275  0.5844655  1.480613993
Oklahoma      36 -0.2727580 -0.2371077  0.1699510 -0.131534211
New Hampshire 29 -1.3059321 -1.3650491 -0.6590781 -1.252564419
Clustering vector:
       Alabama         Alaska        Arizona       Arkansas     California 
             1              2              2              1              2 
      Colorado    Connecticut       Delaware        Florida        Georgia 
             2              3              3              2              1 
        Hawaii          Idaho       Illinois        Indiana           Iowa 
             3              4              2              3              4 
        Kansas       Kentucky      Louisiana          Maine       Maryland 
             3              3              1              4              2 
 Massachusetts       Michigan      Minnesota    Mississippi       Missouri 
             3              2              4              1              3 
       Montana       Nebraska         Nevada  New Hampshire     New Jersey 
             3              3              2              4              3 
    New Mexico       New York North Carolina   North Dakota           Ohio 
             2              2              1              4              3 
      Oklahoma         Oregon   Pennsylvania   Rhode Island South Carolina 
             3              3              3              3              1 
  South Dakota      Tennessee          Texas           Utah        Vermont 
             4              1              2              3              4 
      Virginia     Washington  West Virginia      Wisconsin        Wyoming 
             3              3              4              4              3 
Objective function:
   build     swap 
1.035116 1.027102 

Available components:
 [1] "medoids"    "id.med"     "clustering" "objective"  "isolation" 
 [6] "clusinfo"   "silinfo"    "diss"       "call"       "data"          

Notez que les quatre centroïdes de cluster sont des observations réelles dans l’ensemble de données. Près du haut de la sortie, nous pouvons voir que les quatre centroïdes sont les états suivants :

• Alabama
• Michigan
• Oklahoma
• New Hampshire

Nous pouvons visualiser les clusters sur un nuage de points qui affiche les deux premières composantes principales sur les axes en utilisant la fonction fivz_cluster() :

#plot results of final k-medoids model
fviz_cluster(kmed, data = df)

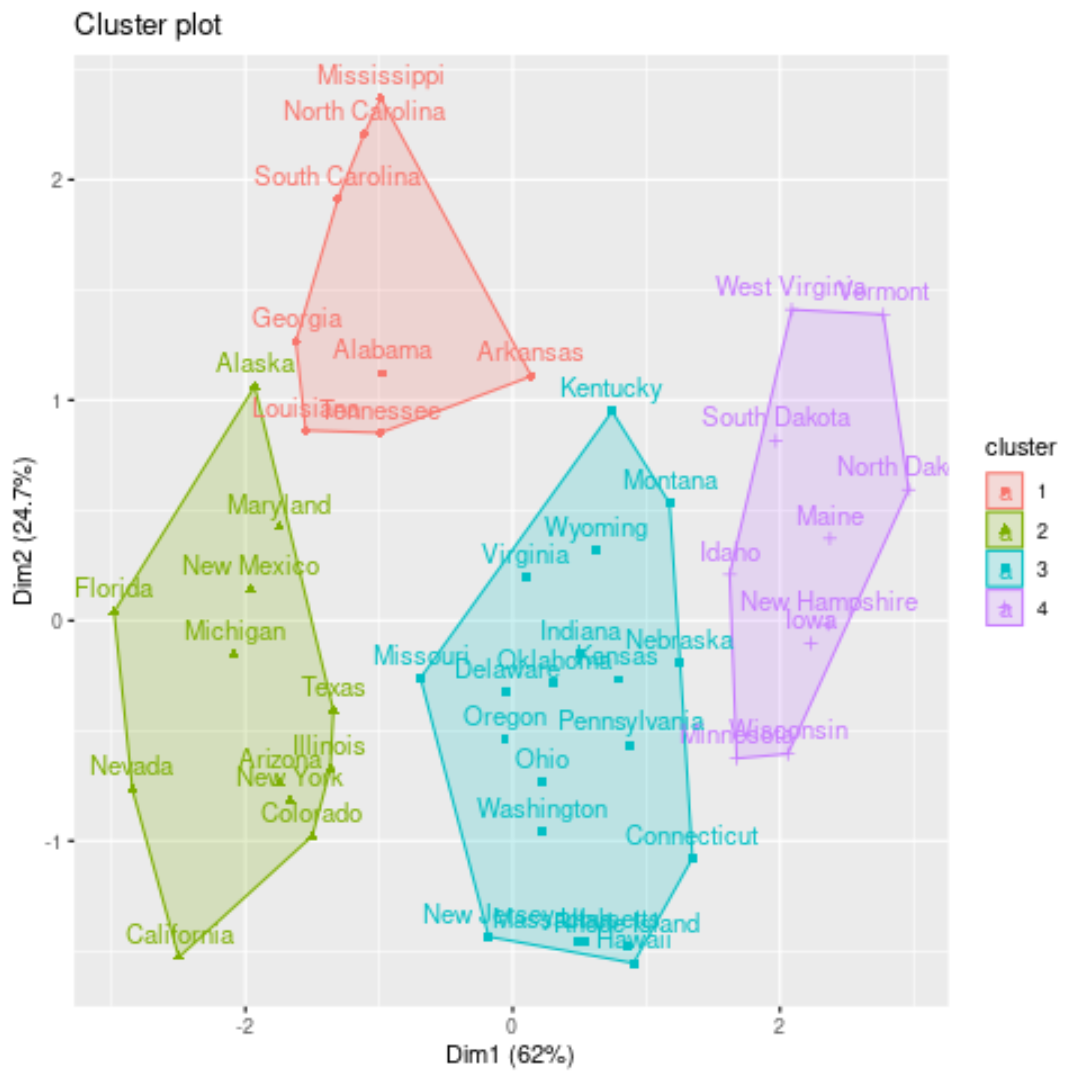
Nous pouvons également ajouter les affectations de cluster de chaque état à l’ensemble de données d’origine :

#add cluster assignment to original data
final_data <- cbind(USArrests, cluster = kmed$cluster)

#view final data
head(final_data)

           Murder Assault UrbanPop Rape cluster
Alabama      13.2     236       58 21.2       1
Alaska       10.0     263       48 44.5       2
Arizona       8.1     294       80 31.0       2
Arkansas      8.8     190       50 19.5       1
California    9.0     276       91 40.6       2
Colorado      7.9     204       78 38.7       2

Vous pouvez trouver le code R complet utilisé dans cet exemple ici .