Comment effectuer une correction de Bonferroni dans R
Une ANOVA unidirectionnelle est utilisée pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes indépendants ou plus.
Si la valeur p globale du tableau ANOVA est inférieure à un certain niveau de signification, alors nous disposons de preuves suffisantes pour affirmer qu’au moins une des moyennes des groupes est différente des autres.
Cependant, cela ne nous dit pas quels groupes sont différents les uns des autres. Cela nous dit simplement que toutes les moyennes du groupe ne sont pas égales.
Afin de savoir exactement quels groupes sont différents les uns des autres, nous devons effectuer des tests t par paires entre chaque groupe tout en contrôlant le taux d’erreur par famille .
L’un des moyens les plus courants d’y parvenir consiste à utiliser la correction de Bonferroni lors du calcul des valeurs p pour chacun des tests t par paire.
Ce tutoriel explique comment effectuer la correction de Bonferroni dans R.
Exemple : correction de Bonferroni dans R
Supposons qu’un enseignant veuille savoir si trois techniques d’étude différentes conduisent ou non à des résultats d’examen différents parmi les élèves.
Pour tester cela, elle assigne au hasard 10 étudiants pour qu’ils utilisent chaque technique d’étude. Après une semaine d’utilisation de la technique d’étude qui lui a été assignée, chaque étudiant passe le même examen.
Nous pouvons utiliser les étapes suivantes dans R pour ajuster une ANOVA unidirectionnelle et utiliser la correction de Bonferroni pour calculer les différences par paires entre les résultats des examens de chaque groupe.
Étape 1 : Créez l’ensemble de données.
Le code suivant montre comment créer un ensemble de données contenant les résultats des examens des 30 étudiants :
#create data frame data <- data.frame(technique = rep(c("tech1", "tech2", "tech3"), each = 10), score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89, 81, 82, 83, 83, 83, 84, 87, 90, 92, 93, 77, 78, 79, 88, 89, 90, 91, 95, 95, 98)) #view first six rows of data frame head(data) technique score 1 tech1 76 2 tech1 77 3 tech1 77 4 tech1 81 5 tech1 82 6 tech1 82
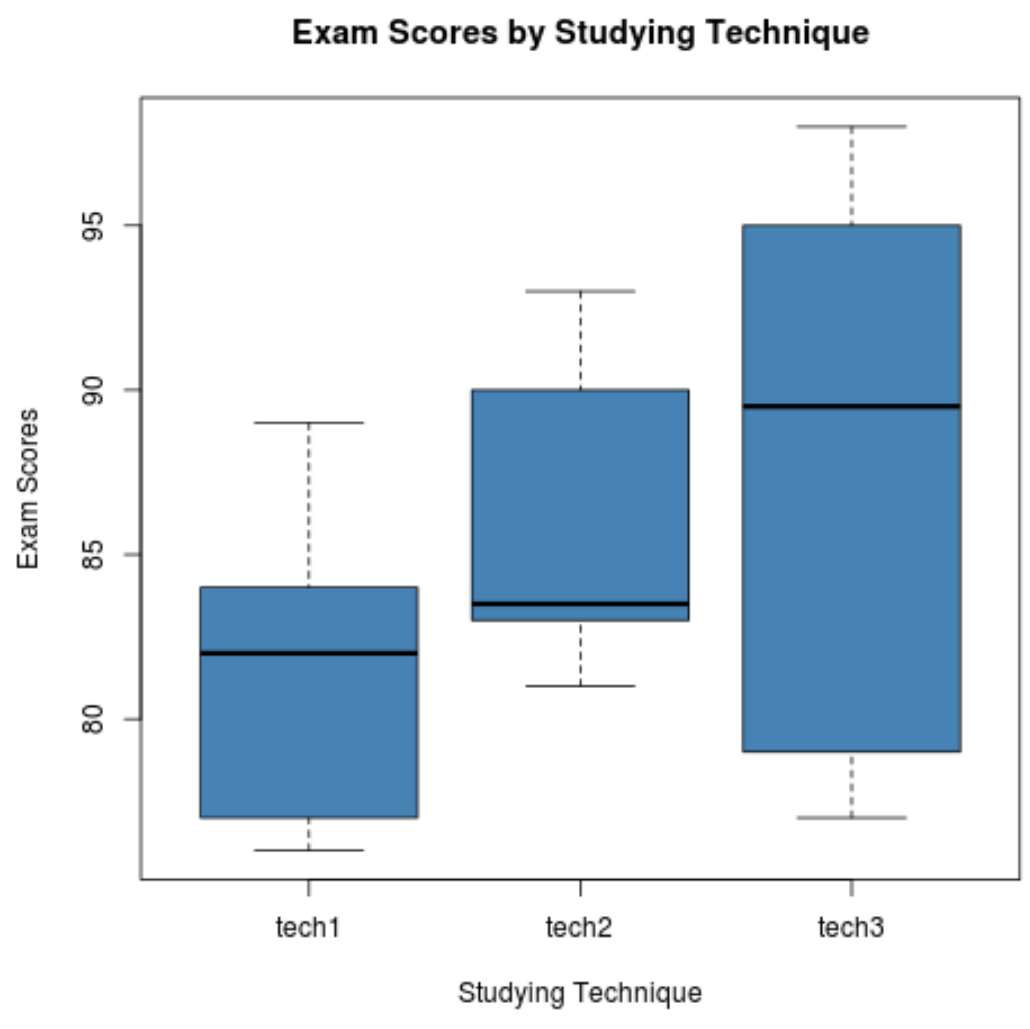
Étape 2 : Visualisez les résultats des examens pour chaque groupe.
Le code suivant montre comment produire des boxplots pour visualiser la distribution des résultats des examens pour chaque groupe :
boxplot(score ~ technique,
data = data,
main = "Exam Scores by Studying Technique",
xlab = "Studying Technique",
ylab = "Exam Scores",
col = "steelblue",
border = "black")
Étape 3 : Effectuez une ANOVA unidirectionnelle.
Le code suivant montre comment effectuer une ANOVA unidirectionnelle pour tester les différences entre les résultats moyens aux examens dans chaque groupe :
#fit the one-way ANOVA model model <- aov(score ~ technique, data = data) #view model output summary(model) Df Sum Sq Mean Sq F value Pr(>F) technique 2 211.5 105.73 3.415 0.0476 * Residuals 27 836.0 30.96 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Étant donné que la valeur p globale ( 0,0476 ) est inférieure à 0,05, cela indique que chaque groupe n’a pas la même note moyenne à l’examen.
Ensuite, nous effectuerons des tests t par paires en utilisant la correction de Bonferroni pour les valeurs p afin de calculer les différences par paires entre les résultats des examens de chaque groupe.
Étape 4 : Effectuez des tests t par paires.
Pour effectuer des tests t par paires avec la correction de Bonferroni dans R, nous pouvons utiliser la fonction pairwise.t.test() , qui utilise la syntaxe suivante :
pairwise.t.test(x, g, p.adjust.method=”bonferroni”)
où:
- x : un vecteur numérique de valeurs de réponse
- g : Un vecteur qui spécifie les noms des groupes (par exemple, étudier la technique)
Le code suivant montre comment utiliser cette fonction pour notre exemple :
#perform pairwise t-tests with Bonferroni's correction pairwise.t.test(data$score, data$technique, p.adjust.method="bonferroni") Pairwise comparisons using t tests with pooled SD data: data$score and data$technique tech1 tech2 tech2 0.309 - tech3 0.048 1.000 P value adjustment method: bonferroni
La façon d’interpréter le résultat est la suivante :
- La valeur p ajustée pour la différence moyenne des résultats aux examens entre la technique 1 et la technique 2 est de 0,309 .
- La valeur p ajustée pour la différence moyenne des résultats aux examens entre la technique 1 et la technique 3 est de 0,048 .
- La valeur p ajustée pour la différence moyenne des résultats aux examens entre la technique 2 et la technique 3 est de 1 000 .
Sur la base des résultats, nous pouvons voir que la seule différence significative se situe entre la technique 1 et la technique 3.
Ressources additionnelles
Une introduction à l’ANOVA unidirectionnelle
Comment effectuer une ANOVA unidirectionnelle dans R
Comment effectuer le test de Tukey dans R
Comment effectuer le test de Dunnett dans R
