Comment interpréter un tracé d’échelle et de localisation : avec des exemples

Un graphique de localisation à l’échelle est un type de graphique qui affiche les valeurs ajustées d’un modèle de régression le long de l’axe des x et la racine carrée des résidus standardisés le long de l’axe des y.

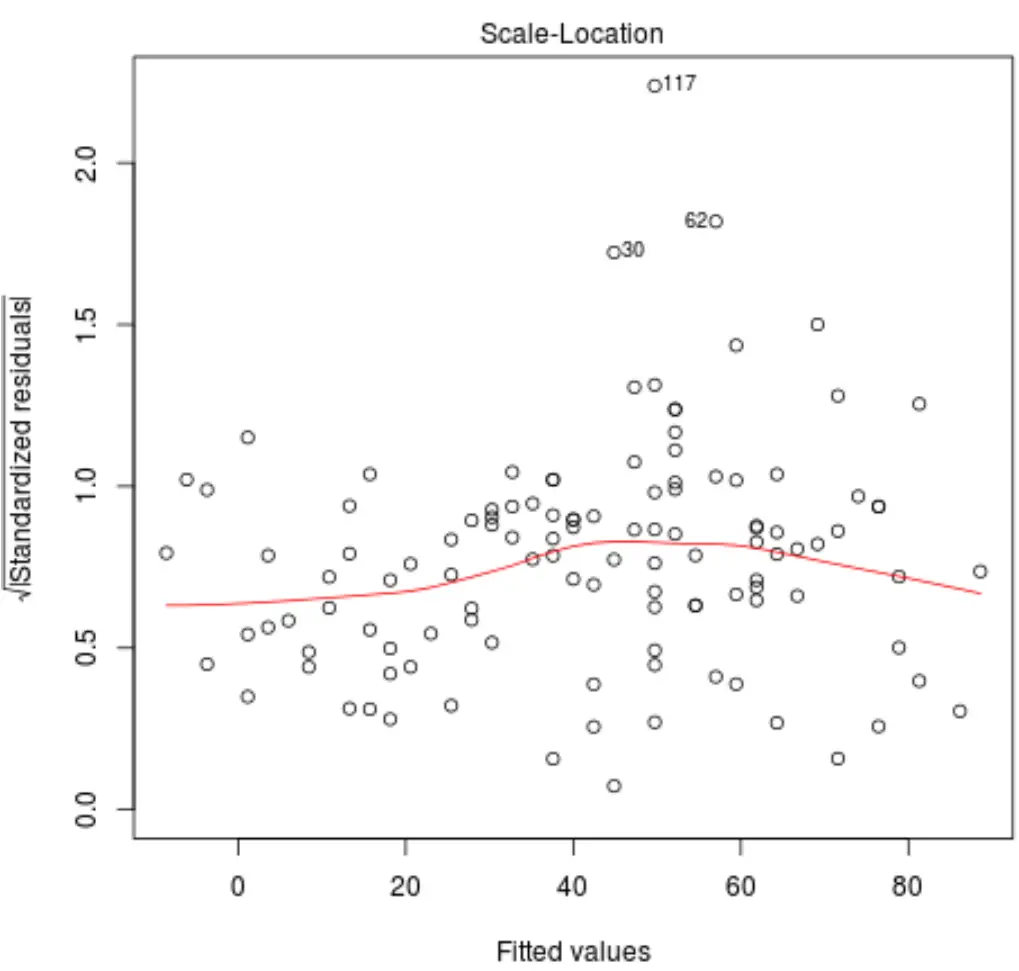
En regardant ce graphique, nous vérifions deux choses :

1. Vérifiez que la ligne rouge est à peu près horizontale sur le tracé. Si tel est le cas, alors l’hypothèse d’ homoscédasticité est probablement satisfaite pour un modèle de régression donné. Autrement dit, la répartition des résidus est à peu près égale pour toutes les valeurs ajustées.

2. Vérifiez qu’il n’y a pas de tendance claire parmi les résidus. En d’autres termes, les résidus doivent être dispersés de manière aléatoire autour de la ligne rouge avec une variabilité à peu près égale pour toutes les valeurs ajustées.

Tracé d’échelle et d’emplacement dans R

Nous pouvons utiliser le code suivant pour ajuster un modèle de régression linéaire simple dans R et produire un tracé d’échelle et de localisation pour le modèle résultant :

#fit simple linear regression model
model <- lm(Ozone ~ Temp, data = airquality)

#produce scale-location plot
plot(model)

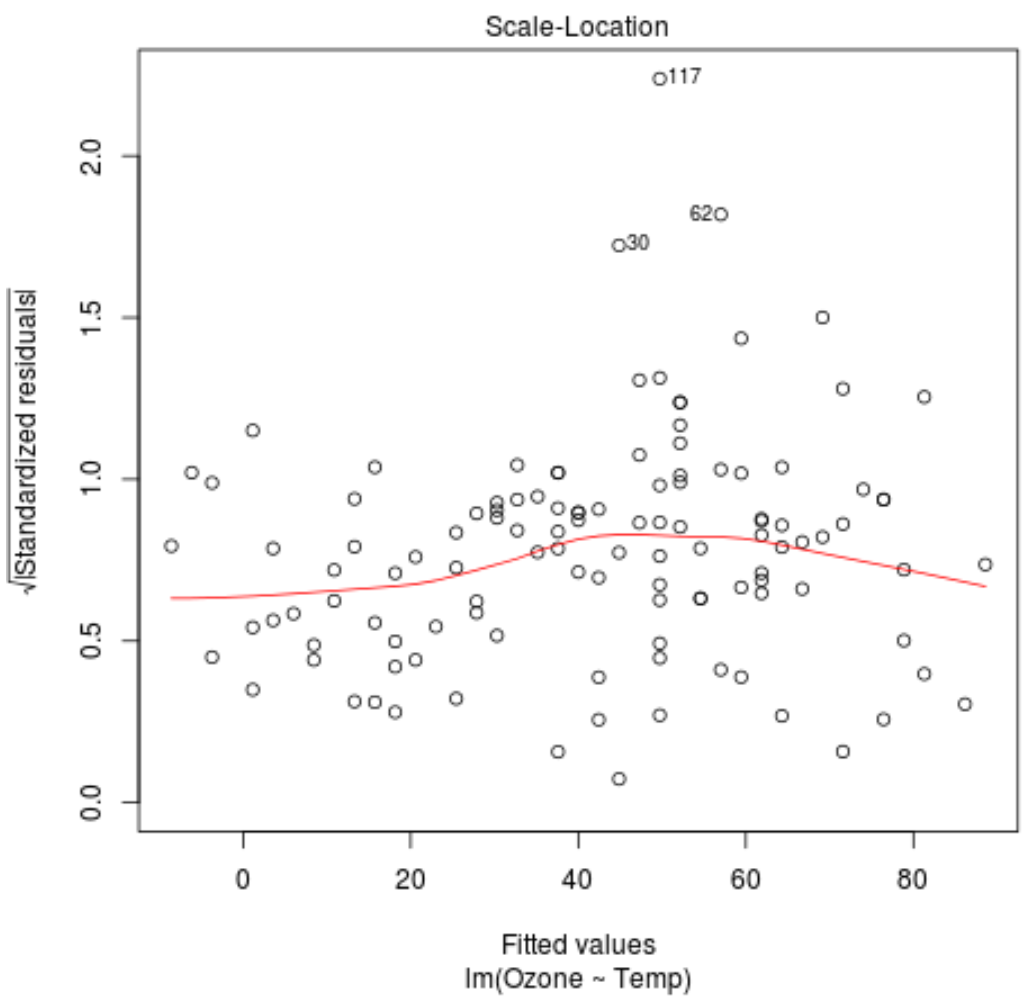
Nous pouvons observer les deux choses suivantes à partir du tracé échelle-emplacement de ce modèle de régression.

1. La ligne rouge est à peu près horizontale sur le tracé. Si tel est le cas, alors l’hypothèse d’ homoscédasticité est satisfaite pour un modèle de régression donné. Autrement dit, la répartition des résidus est à peu près égale pour toutes les valeurs ajustées.

2. Vérifiez qu’il n’y a pas de tendance claire parmi les résidus. En d’autres termes, les résidus doivent être dispersés de manière aléatoire autour de la ligne rouge avec une variabilité à peu près égale pour toutes les valeurs ajustées.

Note technique

Les trois observations de l’ensemble de données avec les résidus standardisés les plus élevés sont étiquetées dans le graphique.

Nous pouvons voir que les observations des lignes 30, 62 et 117 ont les résidus standardisés les plus élevés.

Cela ne signifie pas nécessairement que ces observations sont aberrantes, mais vous souhaiterez peut-être consulter les données originales pour examiner ces observations de plus près.

Bien que nous puissions voir que la ligne rouge est à peu près horizontale sur le tracé de localisation de l’échelle, cela ne sert que de moyen visuel pour voir si l’hypothèse d’homoscédasticité est satisfaite.

Un test statistique formel que nous pouvons utiliser pour voir si l’hypothèse d’homoscédasticité est remplie est le test de Breusch-Pagan .

Test de Breusch-Pagan dans R

Le code suivant montre comment utiliser la fonction bptest() du package lmtest pour effectuer un test de Breusch-Pagan dans R :

#load lmtest package
library(lmtest)

#perform Breusch-Pagan Test
bptest(model)

	studentized Breusch-Pagan test

data:  model
BP = 1.4798, df = 1, p-value = 0.2238

Un test de Breusch-Pagan utilise les hypothèses nulles et alternatives suivantes :

• Hypothèse nulle (H ₀ ) : les résidus sont homoscédastiques (c’est-à-dire uniformément répartis)
• Hypothèse alternative (H _A ) : Les résidus sont hétéroscédastiques (c’est-à-dire non répartis uniformément)

À partir du résultat, nous pouvons voir que la valeur p du test est 0,2238 . Puisque cette valeur p n’est pas inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle. Nous ne disposons pas de preuves suffisantes pour affirmer que l’hétéroscédasticité est présente dans le modèle de régression.

Ce résultat correspond à notre inspection visuelle de la ligne rouge dans le tracé d’échelle-emplacement.

Ressources additionnelles

Comprendre l’hétéroscédasticité dans l’analyse de régression
Comment créer un tracé résiduel dans R
Comment effectuer un test de Breusch-Pagan dans R