Comment créer des forêts aléatoires dans R (étape par étape)

Lorsque la relation entre un ensemble de variables prédictives et une variable de réponse est très complexe, nous utilisons souvent des méthodes non linéaires pour modéliser la relation entre elles.

Une de ces méthodes consiste à construire un arbre de décision . Cependant, l’inconvénient de l’utilisation d’un seul arbre de décision est qu’il a tendance à souffrir d’ une variance élevée .

Autrement dit, si nous divisons l’ensemble de données en deux moitiés et appliquons l’arbre de décision aux deux moitiés, les résultats pourraient être très différents.

Une méthode que nous pouvons utiliser pour réduire la variance d’un seul arbre de décision consiste à construire un modèle de forêt aléatoire , qui fonctionne comme suit :

1. Prenez b échantillons bootstrapés à partir de l’ensemble de données d’origine.

2. Créez un arbre de décision pour chaque échantillon bootstrap.

• Lors de la construction de l’arbre, chaque fois qu’une division est prise en compte, seul un échantillon aléatoire de m prédicteurs est considéré comme candidat à la division parmi l’ensemble complet des p prédicteurs. Généralement, nous choisissons m égal à √ p .

3. Faites la moyenne des prédictions de chaque arbre pour obtenir un modèle final.

Il s’avère que les forêts aléatoires ont tendance à produire des modèles beaucoup plus précis que les arbres de décision uniques et même les modèles en sac .

Ce didacticiel fournit un exemple étape par étape de la façon de créer un modèle de forêt aléatoire pour un ensemble de données dans R.

Étape 1 : Chargez les packages nécessaires

Tout d’abord, nous allons charger les packages nécessaires pour cet exemple. Pour cet exemple simple, nous n’avons besoin que d’un seul package :

library(randomForest)

Étape 2 : Ajuster le modèle de forêt aléatoire

Pour cet exemple, nous utiliserons un ensemble de données R intégré appelé qualité de l’air qui contient des mesures de la qualité de l’air à New York sur 153 jours individuels.

#view structure of airquality dataset
str(airquality)

'data.frame':	153 obs. of  6 variables:
 $ Ozone  : int  41 36 12 18 NA 28 23 19 8 NA ...
 $ Solar.R: int  190 118 149 313 NA NA 299 99 19 194 ...
 $ Wind   : num  7.4 8 12.6 11.5 14.3 14.9 8.6 13.8 20.1 8.6 ...
 $ Temp   : int  67 72 74 62 56 66 65 59 61 69 ...
 $ Month  : int  5 5 5 5 5 5 5 5 5 5 ...
 $ Day    : int  1 2 3 4 5 6 7 8 9 10 ...

#find number of rows with missing values
sum(!complete.cases(airquality))

[1] 42

Cet ensemble de données comporte 42 lignes avec des valeurs manquantes. Par conséquent, avant d’ajuster un modèle de forêt aléatoire, nous remplirons les valeurs manquantes dans chaque colonne avec les médianes des colonnes :

#replace NAs with column medians
for(i in 1:ncol(airquality)) {
  airquality[ , i][is.na(airquality[ , i])] <- median(airquality[ , i], na.rm=TRUE)
}

Connexes : Comment imputer les valeurs manquantes dans R

Le code suivant montre comment ajuster un modèle de forêt aléatoire dans R à l’aide de la fonction randomForest() du package randomForest .

#make this example reproducible
set.seed(1)

#fit the random forest model
model <- randomForest(
  formula = Ozone ~ .,
  data = airquality
)

#display fitted model
model

Call:
 randomForest(formula = Ozone ~ ., data = airquality) 
               Type of random forest: regression
                     Number of trees: 500
No. of variables tried at each split: 1

          Mean of squared residuals: 327.0914
                    % Var explained: 61

#find number of trees that produce lowest test MSE
which.min(model$mse)

[1] 82

#find RMSE of best model
sqrt(model$mse[which.min(model$mse)]) 

[1] 17.64392

À partir du résultat, nous pouvons voir que le modèle qui a produit l’erreur quadratique moyenne (MSE) de test la plus faible a utilisé 82 arbres.

Nous pouvons également voir que l’erreur quadratique moyenne de ce modèle était de 17,64392 . Nous pouvons considérer cela comme la différence moyenne entre la valeur prévue pour l’ozone et la valeur réelle observée.

Nous pouvons également utiliser le code suivant pour produire un tracé du test MSE basé sur le nombre d’arbres utilisés :

#plot the test MSE by number of trees
plot(model)

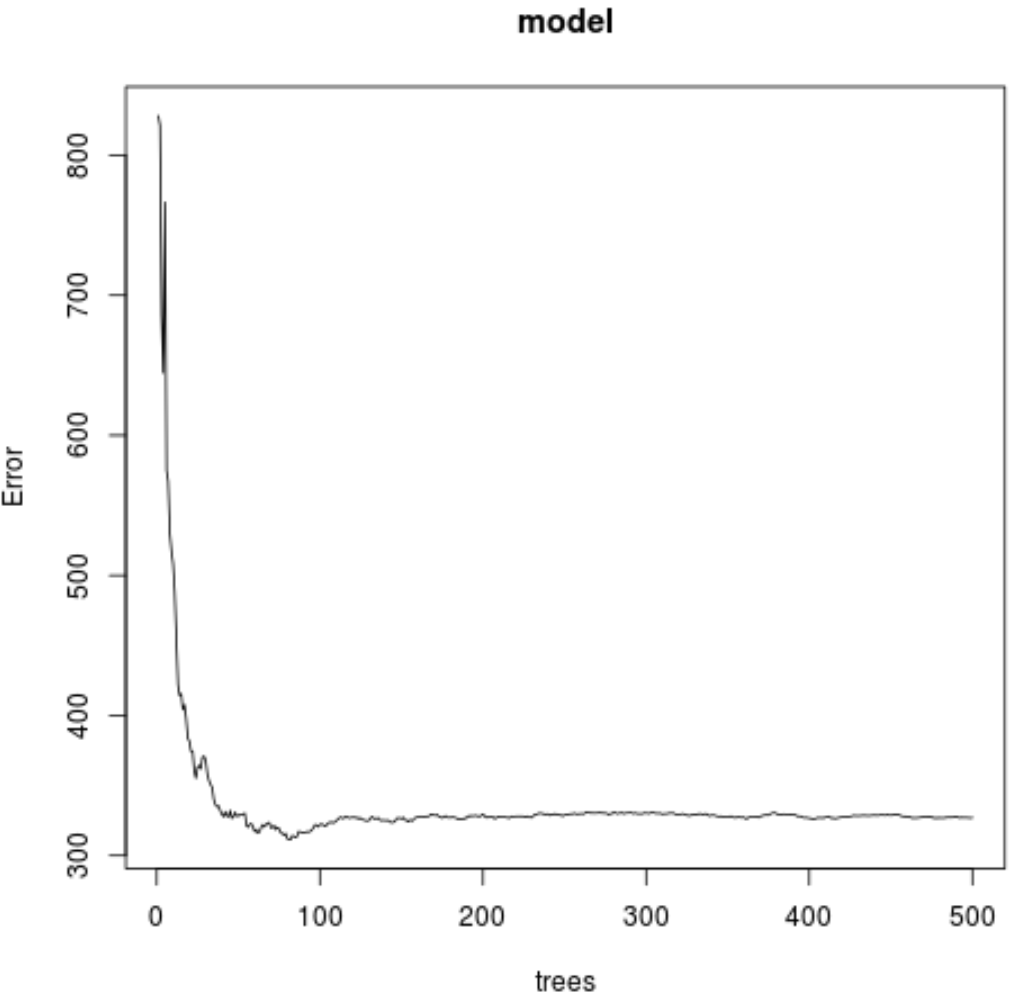
Et nous pouvons utiliser la fonction varImpPlot() pour créer un tracé qui affiche l’importance de chaque variable prédictive dans le modèle final :

#produce variable importance plot
varImpPlot(model) 

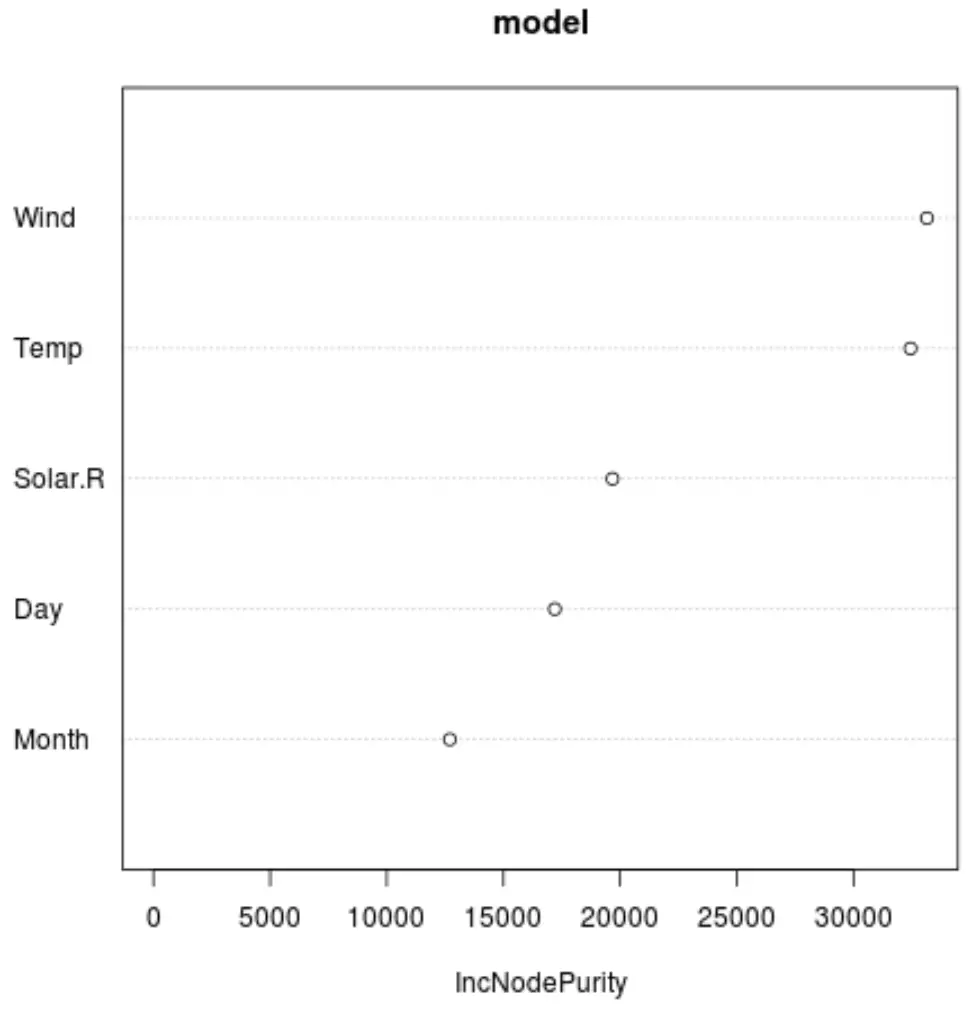
L’axe des x affiche l’augmentation moyenne de la pureté des nœuds des arbres de régression en fonction de la division sur les différents prédicteurs affichés sur l’axe des y.

D’après le graphique, nous pouvons voir que Wind est la variable prédictive la plus importante, suivie de près par Temp .

Étape 3 : Ajuster le modèle

Par défaut, la fonction randomForest() utilise 500 arbres et (total de prédicteurs/3) prédicteurs sélectionnés au hasard comme candidats potentiels à chaque division. Nous pouvons ajuster ces paramètres en utilisant la fonction tuneRF() .

Le code suivant montre comment trouver le modèle optimal à l’aide des spécifications suivantes :

• ntreeTry : Le nombre d’arbres à construire.
• mtryStart : le nombre initial de variables prédictives à prendre en compte à chaque division.
• stepFactor : facteur à augmenter jusqu’à ce que l’erreur estimée hors du sac cesse de s’améliorer d’un certain montant.
• améliorer : le montant dont l’erreur de sortie du sac doit être améliorée pour continuer à augmenter le facteur de pas.

model_tuned <- tuneRF(
               x=airquality[,-1], #define predictor variables
               y=airquality$Ozone, #define response variable
               ntreeTry=500,
               mtryStart=4, 
               stepFactor=1.5,
               improve=0.01,
               trace=FALSE #don't show real-time progress
               )

Cette fonction produit le tracé suivant, qui affiche le nombre de prédicteurs utilisés à chaque division lors de la construction des arbres sur l’axe des x et l’erreur estimée hors sac sur l’axe des y :

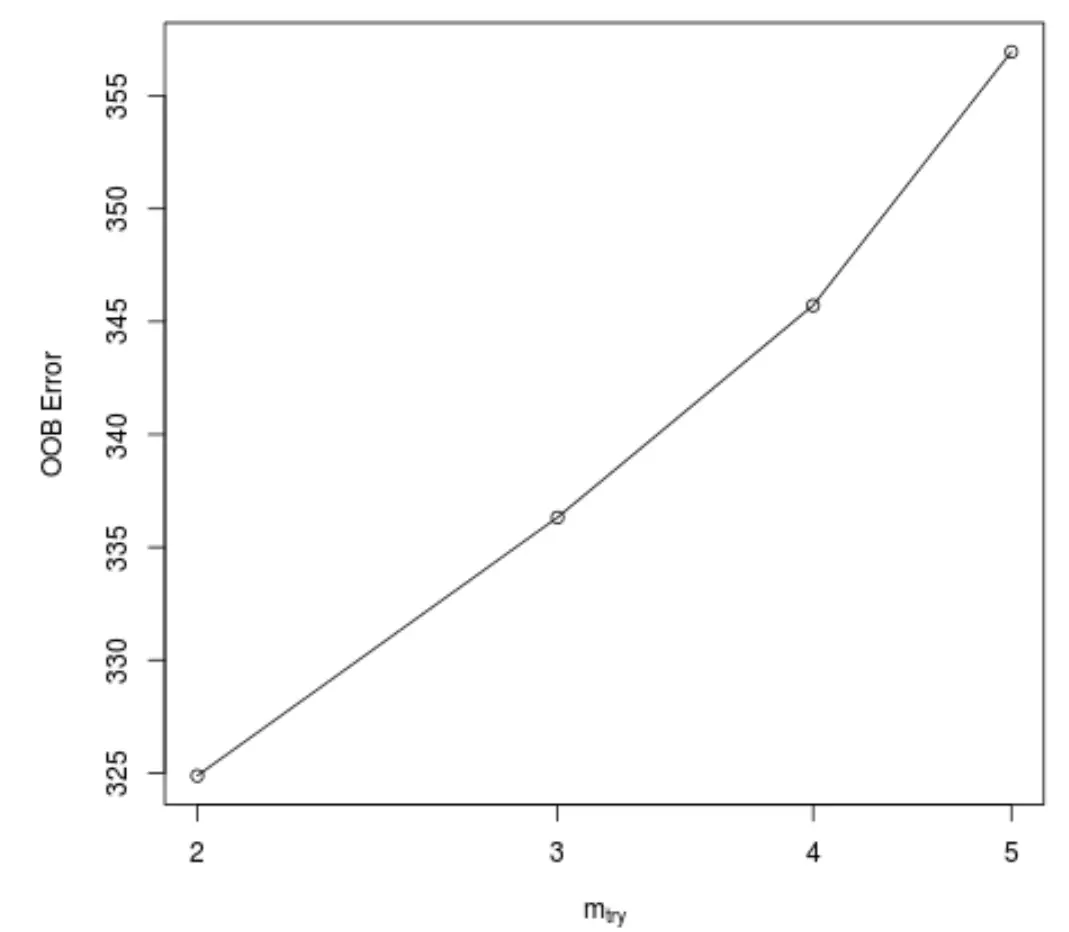
Nous pouvons voir que l’erreur OOB la plus faible est obtenue en utilisant 2 prédicteurs choisis au hasard à chaque division lors de la construction des arbres.

Cela correspond en fait au paramètre par défaut (total des prédicteurs/3 = 6/3 = 2) utilisé par la fonction randomForest() initiale.

Étape 4 : Utiliser le modèle final pour faire des prédictions

Enfin, nous pouvons utiliser le modèle de forêt aléatoire ajusté pour faire des prédictions sur de nouvelles observations.

#define new observation
new <- data.frame(Solar.R=150, Wind=8, Temp=70, Month=5, Day=5)

#use fitted bagged model to predict Ozone value of new observation
predict(model, newdata=new)

27.19442

Sur la base des valeurs des variables prédictives, le modèle de forêt aléatoire ajusté prédit que la valeur de l’ozone sera de 27,19442 ce jour particulier.

Le code R complet utilisé dans cet exemple peut être trouvé ici .