Comment effectuer le test t de Welch dans R

Le test t de Welch est utilisé pour comparer les moyennes entre deux groupes indépendants lorsqu’on ne suppose pas que les deux groupes ont des variances égales.

Pour effectuer le test t de Welch dans R, nous pouvons utiliser la fonction t.test() , qui utilise la syntaxe suivante :

t.test(x, y, alternative = c(« deux faces », « moins », « plus grand »))

où:

• x : un vecteur numérique de valeurs de données pour le premier groupe
• y : un vecteur numérique de valeurs de données pour le deuxième groupe
• alternative : l’hypothèse alternative pour le test. La valeur par défaut est recto verso.

L’exemple suivant montre comment utiliser cette fonction pour effectuer le test t de Welch dans R.

Exemple : test t de Welch dans R

Un enseignant souhaite comparer les résultats d’examen de 12 élèves qui ont utilisé un livret de préparation à l’examen pour se préparer à un examen par rapport à 12 élèves qui ne l’ont pas fait.

Les vecteurs suivants montrent les résultats des examens des étudiants de chaque groupe :

booklet <- c(90, 85, 88, 89, 94, 91, 79, 83, 87, 88, 91, 90)
no_booklet <- c(67, 90, 71, 95, 88, 83, 72, 66, 75, 86, 93, 84)

Avant d’effectuer un test t de Welch, nous pouvons d’abord créer des boxplots pour visualiser la distribution des scores pour chaque groupe :

boxplot(booklet, no_booklet, names=c("Booklet","No Booklet"))

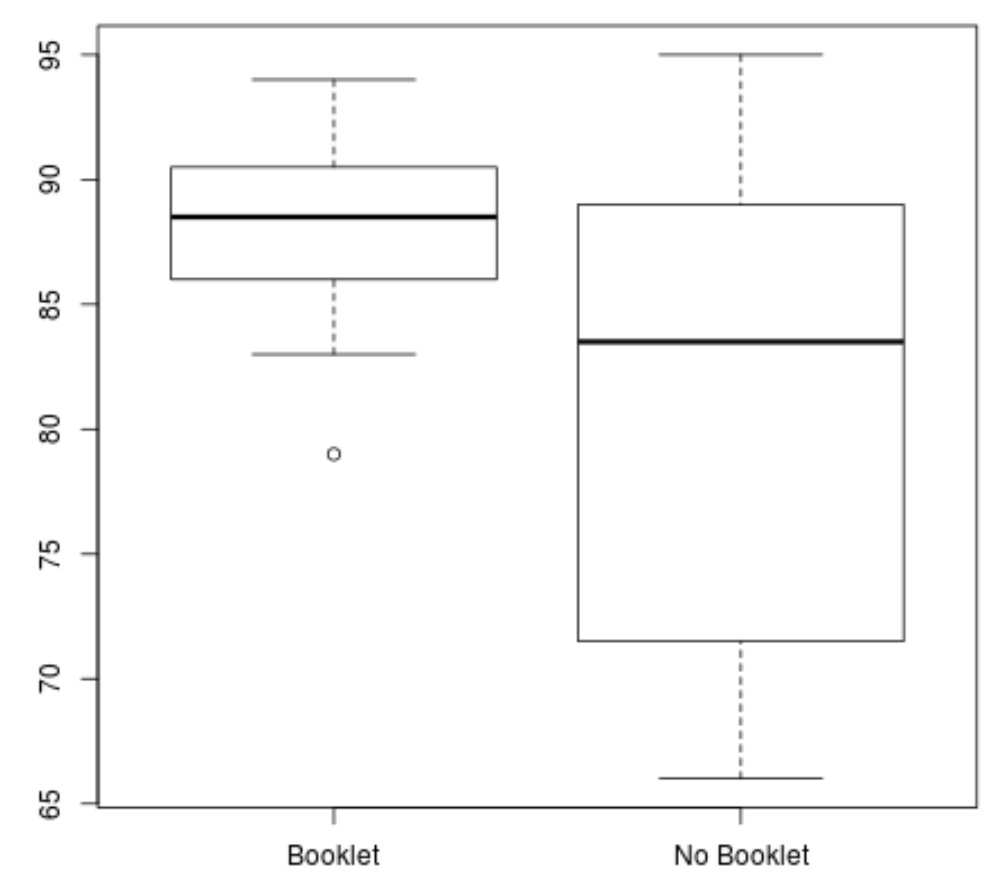
On voit clairement que le groupe « Livret » a un score moyen plus élevé et une variance des scores plus faible.

Pour tester formellement si les scores moyens entre les groupes sont significativement différents, nous pouvons effectuer le test t de Welch :

#perform Welch's t-test
t.test(booklet, no_booklet)

	Welch Two Sample t-test

data:  booklet and no_booklet
t = 2.2361, df = 14.354, p-value = 0.04171
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
  0.3048395 13.8618272
sample estimates:
mean of x mean of y 
 87.91667  80.83333 

À partir du résultat, nous pouvons voir que la statistique du test t est de 2,2361 et la valeur p correspondante est de 0,04171 .

Puisque cette valeur p est inférieure à 0,05, nous pouvons rejeter l’hypothèse nulle et conclure qu’il existe une différence statistiquement significative dans les résultats moyens aux examens entre les deux groupes.

La fonction t.test() nous fournit également les informations suivantes :

• L’ intervalle de confiance à 95 % pour la différence des scores moyens aux examens entre les deux groupes est de [0,3048, 13,8618 ].
• La note moyenne à l’examen du premier groupe est de 87,91667 .
• La note moyenne à l’examen du deuxième groupe est de 80,83333 .

Vous pouvez trouver la documentation complète de la fonction t.test() ici .

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans R :

Comment effectuer un test t sur un échantillon dans R
Comment effectuer un test t à deux échantillons dans R
Comment effectuer un test t pour échantillons appariés dans R
Comment tracer plusieurs boîtes à moustaches dans un seul graphique dans R