Comment effectuer un test de corrélation dans R (avec exemples)

Une façon de quantifier la relation entre deux variables consiste à utiliser le coefficient de corrélation de Pearson , qui est une mesure de l’association linéaire entre deux variables .

Il prend toujours une valeur comprise entre -1 et 1 où :

• -1 indique une corrélation linéaire parfaitement négative entre deux variables
• 0 indique aucune corrélation linéaire entre deux variables
• 1 indique une corrélation linéaire parfaitement positive entre deux variables

Pour déterminer si un coefficient de corrélation est statistiquement significatif, vous pouvez calculer le score t et la valeur p correspondants.

La formule pour calculer le t-score d’un coefficient de corrélation (r) est :

t = r * √ n-2 / √ 1-r ²

La valeur p est calculée comme la valeur p bilatérale correspondante pour la distribution t avec n-2 degrés de liberté.

Exemple : test de corrélation dans R

Pour déterminer si le coefficient de corrélation entre deux variables est statistiquement significatif, vous pouvez effectuer un test de corrélation dans R en utilisant la syntaxe suivante :

cor.test(x, y, method=c(« pearson », « kendall », « spearman »))

où:

• x, y : vecteurs numériques de données.
• méthode : Méthode utilisée pour calculer la corrélation entre deux vecteurs. La valeur par défaut est « Pearson ».

Par exemple, supposons que nous ayons les deux vecteurs suivants dans R :

x <- c(2, 3, 3, 5, 6, 9, 14, 15, 19, 21, 22, 23)
y <- c(23, 24, 24, 23, 17, 28, 38, 34, 35, 39, 41, 43)

Avant d’effectuer un test de corrélation entre les deux variables, nous pouvons créer un nuage de points rapide pour visualiser leur relation :

#create scatterplot 
plot(x, y, pch=16)

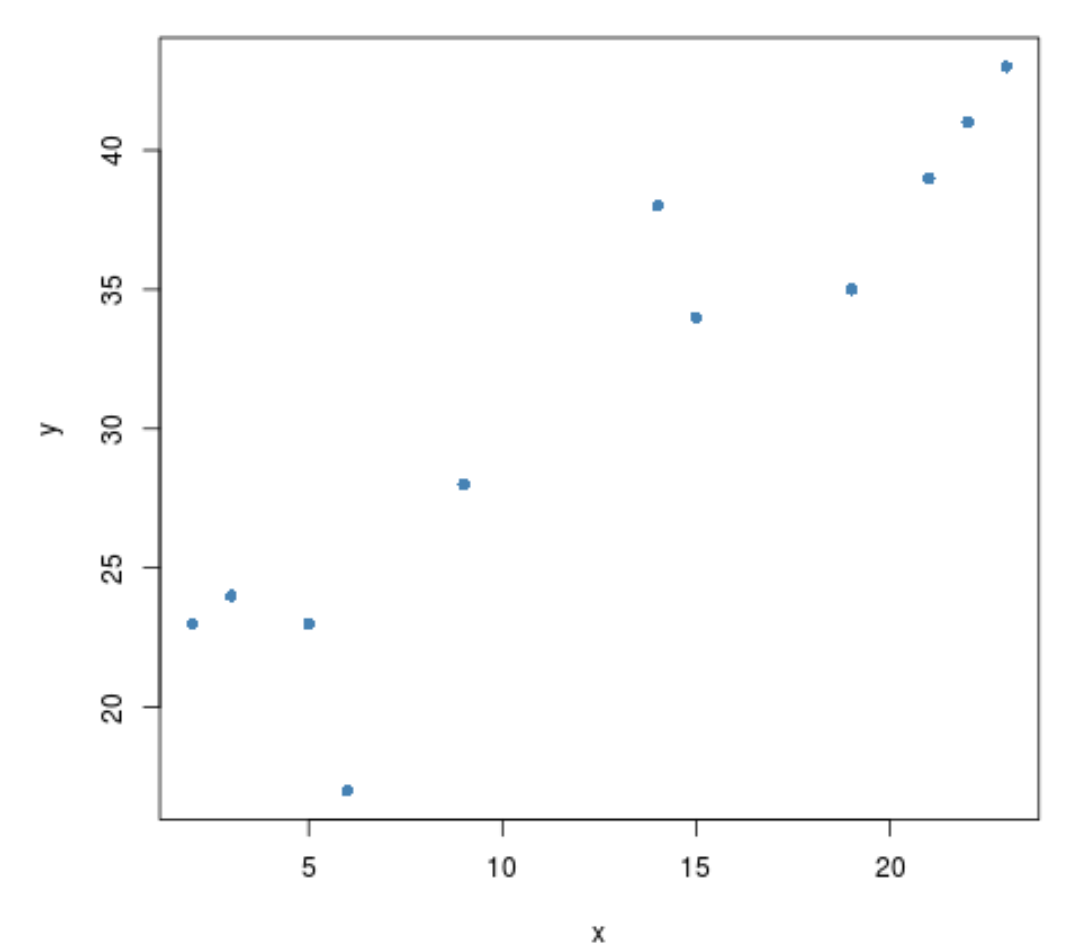
Il semble y avoir une corrélation positive entre les deux variables. Autrement dit, à mesure que l’un augmente, l’autre tend à augmenter également.

Pour voir si cette corrélation est statistiquement significative, nous pouvons effectuer un test de corrélation :

#perform correlation test between the two vectors
cor.test(x, y)

	Pearson's product-moment correlation

data:  x and y
t = 7.8756, df = 10, p-value = 1.35e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7575203 0.9799783
sample estimates:
      cor 
0.9279869 

Le coefficient de corrélation entre les deux vecteurs s’avère être de 0,9279869 .

La statistique du test s’avère être de 7,8756 et la valeur p correspondante est de 1,35e-05 .

Puisque cette valeur est inférieure à 0,05, nous disposons de suffisamment de preuves pour affirmer que la corrélation entre les deux variables est statistiquement significative.

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur les coefficients de corrélation :

Une introduction au coefficient de corrélation de Pearson
Qu’est-ce qui est considéré comme une corrélation « forte » ?
Les cinq hypothèses de la corrélation de Pearson