Comment créer une matrice de corrélation dans Google Sheets

Une façon de quantifier la relation entre deux variables consiste à utiliser le coefficient de corrélation de Pearson , qui est une mesure de l’association linéaire entre deux variables . Il a une valeur comprise entre -1 et 1 où :

• -1 indique une corrélation linéaire parfaitement négative entre deux variables
• 0 indique aucune corrélation linéaire entre deux variables
• 1 indique une corrélation linéaire parfaitement positive entre deux variables

Plus le coefficient de corrélation s’éloigne de zéro, plus la relation entre les deux variables est forte.

Mais dans certains cas, nous souhaitons comprendre la corrélation entre plusieurs paires de variables. Dans ces cas, nous pouvons créer une matrice de corrélation , qui est un tableau carré qui montre les coefficients de corrélation entre plusieurs combinaisons de variables par paires.

Ce tutoriel explique comment créer et interpréter une matrice de corrélation dans Google Sheets.

Comment créer une matrice de corrélation dans Google Sheets

Supposons que nous ayons l’ensemble de données suivant qui montre le nombre moyen de points, de rebonds et de passes décisives pour 10 joueurs de basket-ball :

Pour créer une matrice de corrélation pour cet ensemble de données, nous pouvons utiliser la fonction CORREL() avec la syntaxe suivante :

  COVAR(données_y, données_x)

La matrice de covariance de cet ensemble de données est affichée dans les cellules B15 : D17 tandis que les formules utilisées pour créer la matrice de covariance sont présentées dans les cellules B21 : D23 ci-dessous :

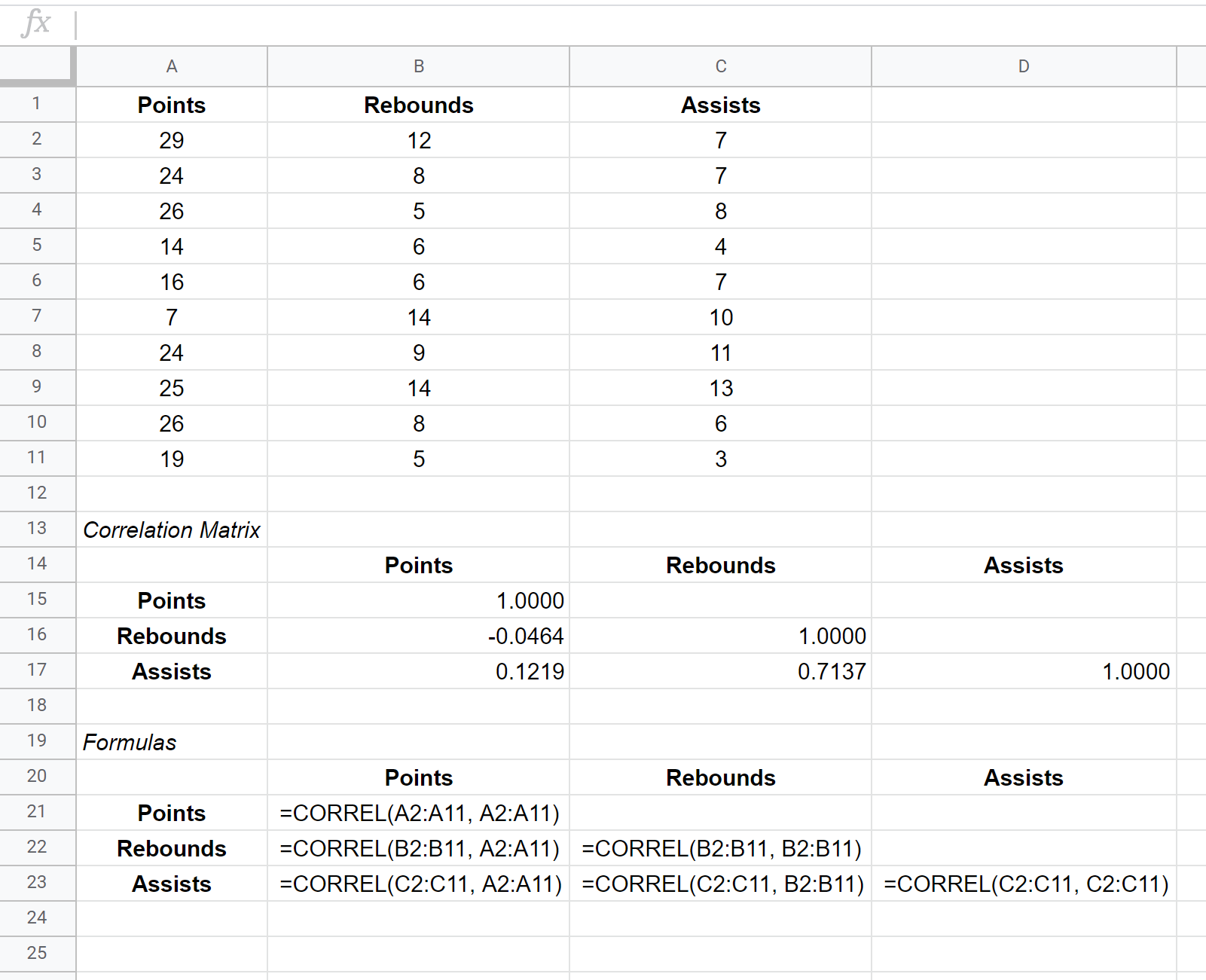
Comment interpréter une matrice de corrélation

Les valeurs dans les cellules individuelles de la matrice de corrélation nous indiquent le coefficient de corrélation de Pearson entre chaque combinaison de variables par paire. Par exemple:

Corrélation entre points et rebonds : -0,0464. Les points et les rebonds sont légèrement corrélés négativement, mais cette valeur est si proche de zéro qu’il n’existe pas de preuves solides d’une association significative entre ces deux variables.

Corrélation entre points et passes décisives : 0,1219. Les points et les passes décisives sont légèrement corrélés positivement, mais cette valeur est également assez proche de zéro, il n’existe donc pas de preuves solides d’une association significative entre ces deux variables.

Corrélation entre rebonds et passes décisives : 0,7137. Les rebonds et les passes décisives sont fortement corrélés positivement. Autrement dit, les joueurs qui ont plus de rebonds ont également tendance à avoir plus de passes décisives.

Notez que les valeurs diagonales de la matrice de corrélation sont toutes égales à 1 car la corrélation entre une variable et elle-même est toujours 1. En pratique, ce nombre n’est pas utile à interpréter.

Ressources additionnelles

Comment lire une matrice de corrélation
Comment créer une matrice de corrélation dans Excel