Qu’est-ce que la corrélation d’ordre zéro ?

En statistique, la corrélation entre deux variables nous renseigne sur la relation entre ces deux variables.

L’un des types de corrélation les plus élémentaires est connu sous le nom de corrélation d’ordre zéro , qui fait référence à la corrélation entre deux variables sans contrôler l’influence possible d’autres variables.

Un exemple de ce type de corrélation est le coefficient de corrélation de Pearson , qui mesure l’association linéaire entre deux variables et peut prendre des valeurs comprises entre -1 et 1 où :

• -1 indique une corrélation linéaire parfaitement négative entre deux variables
• 0 indique aucune corrélation linéaire entre deux variables
• 1 indique une corrélation linéaire parfaitement positive entre deux variables

Plus la corrélation s’éloigne de zéro, plus l’association entre les deux variables est forte.

Corrélations du premier et du deuxième ordre

Si nous calculons la corrélation entre deux variables A et B tout en contrôlant l’influence d’une troisième variable C, nous qualifierions la corrélation entre A et B de corrélation de premier ordre .

De même, si nous calculons la corrélation entre deux variables A et B tout en contrôlant l’influence des variables C et D, nous qualifierions la corrélation entre A et B de corrélation de second ordre .

Exemple de corrélation d’ordre zéro

Supposons que nous disposions de l’ensemble de données suivant qui montre le nombre d’heures passées à étudier et la note obtenue à l’examen par 10 étudiants différents :

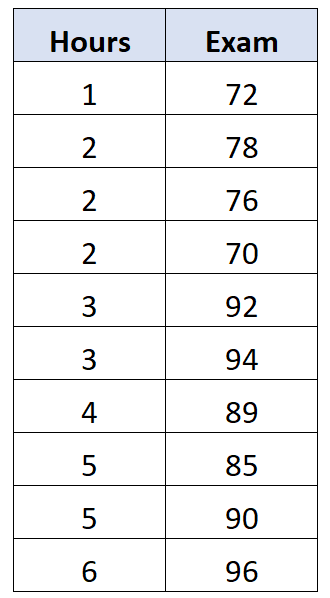
Il s’avère que la corrélation entre ces deux variables est de 0,762 . Cela serait considéré comme une corrélation d’ordre zéro entre les deux variables, car nous ne contrôlons pas l’influence potentielle d’une troisième variable.

Cependant, en réalité, il est possible que d’autres facteurs affectent la relation entre ces deux variables.

Par exemple, la note actuelle de l’élève dans la classe a peut-être un effet sur sa note à l’examen. Supposons que nous ayons également accès à ces données :

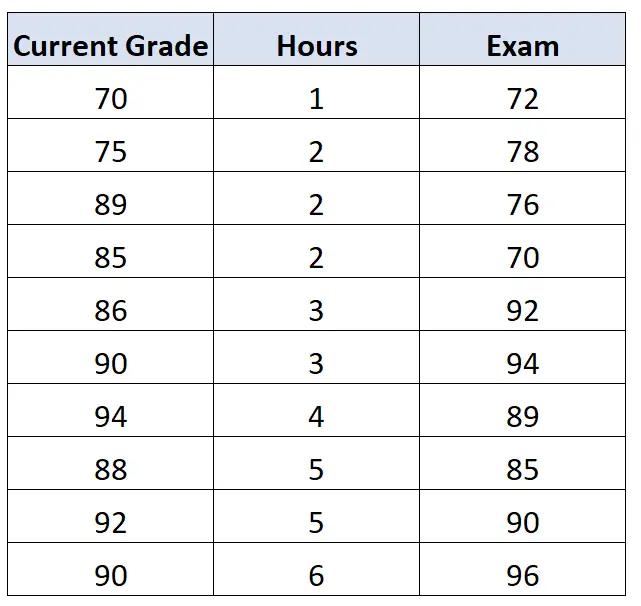
Si nous calculions ensuite la corrélation entre les heures et l’examen tout en contrôlant l’effet de la note actuelle , nous constaterions que la corrélation de premier ordre entre les heures et l’examen est de 0,578 .

Cela signifie qu’il existe toujours une corrélation positive assez forte entre les heures étudiées et la note obtenue à l’examen, même après avoir contrôlé l’effet de la note actuelle de l’étudiant dans la classe.

Remarque : La corrélation de premier ordre est parfois appelée corrélation partielle . Ce tutoriel explique comment calculer des corrélations partielles dans Excel.

Corrélations d’ordre zéro dans une matrice de corrélation

Chaque fois que nous créons une matrice de corrélation pour un ensemble de variables, les coefficients de corrélation affichés dans la matrice sont toujours des corrélations d’ordre zéro car il s’agit simplement des corrélations entre chaque combinaison de variables par paire sans tenir compte de l’influence d’autres variables.

Par exemple, considérons notre ensemble de données de l’exemple précédent :

Si nous créions une matrice de corrélation pour cet ensemble de données, elle ressemblerait à ceci :

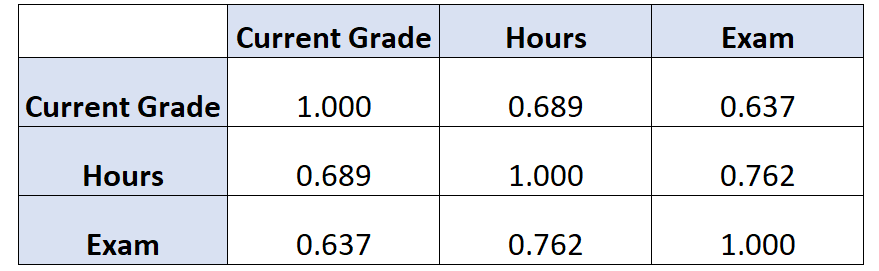
La façon d’interpréter cela est la suivante :

• La corrélation entre la note actuelle et les heures étudiées est de 0,689 .
• La corrélation entre la note actuelle et la note obtenue à l’examen est de 0,637 .
• La corrélation entre les heures étudiées et la note obtenue à l’examen est de 0,762 .

Chacune de ces corrélations est une corrélation d’ordre zéro .

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur les coefficients de corrélation :

Introduction au coefficient de corrélation de Pearson
Comment lire une matrice de corrélation
Comment calculer une corrélation partielle dans Excel