Qu’est-ce que l’échantillonnage Latin Hypercube ?
L’échantillonnage hypercube latin est une méthode qui peut être utilisée pour échantillonner des nombres aléatoires dans lesquels les échantillons sont répartis uniformément sur un espace échantillon.
Il est largement utilisé pour générer des échantillons appelés échantillons aléatoires contrôlés et est souvent appliqué dans l’analyse de Monte Carlo car il peut réduire considérablement le nombre de simulations nécessaires pour obtenir des résultats précis.
Exemple d’introduction
Pour comprendre l’idée de l’échantillonnage hypercube latin, considérons l’exemple simple suivant :
Supposons que nous souhaitions obtenir un échantillon de 2 valeurs à partir d’un ensemble de données normalement distribué avec une moyenne de 0 et un écart type de 1.
Si nous avons utilisé un véritable générateur de nombres aléatoires pour obtenir cet échantillon, il est possible que les deux valeurs soient supérieures à 0 ou que les deux valeurs soient inférieures à 0.
Cependant, si nous utilisions l’échantillonnage d’hypercube latin pour obtenir cet échantillon, il serait alors garanti qu’une valeur serait supérieure à 0 et une autre inférieure à 0, car nous pourrions spécifiquement partitionner l’ espace échantillon en une région avec des valeurs supérieures à 0 et une région avec des valeurs inférieur à 0, puis sélectionnez un échantillon aléatoire dans chaque région.
Échantillonnage d’hypercube latin unidimensionnel
L’idée derrière l’échantillonnage hypercube latin unidimensionnel est simple : divisez un CDF donné en n régions différentes et choisissez au hasard une valeur dans chaque région pour obtenir un échantillon de taille n .
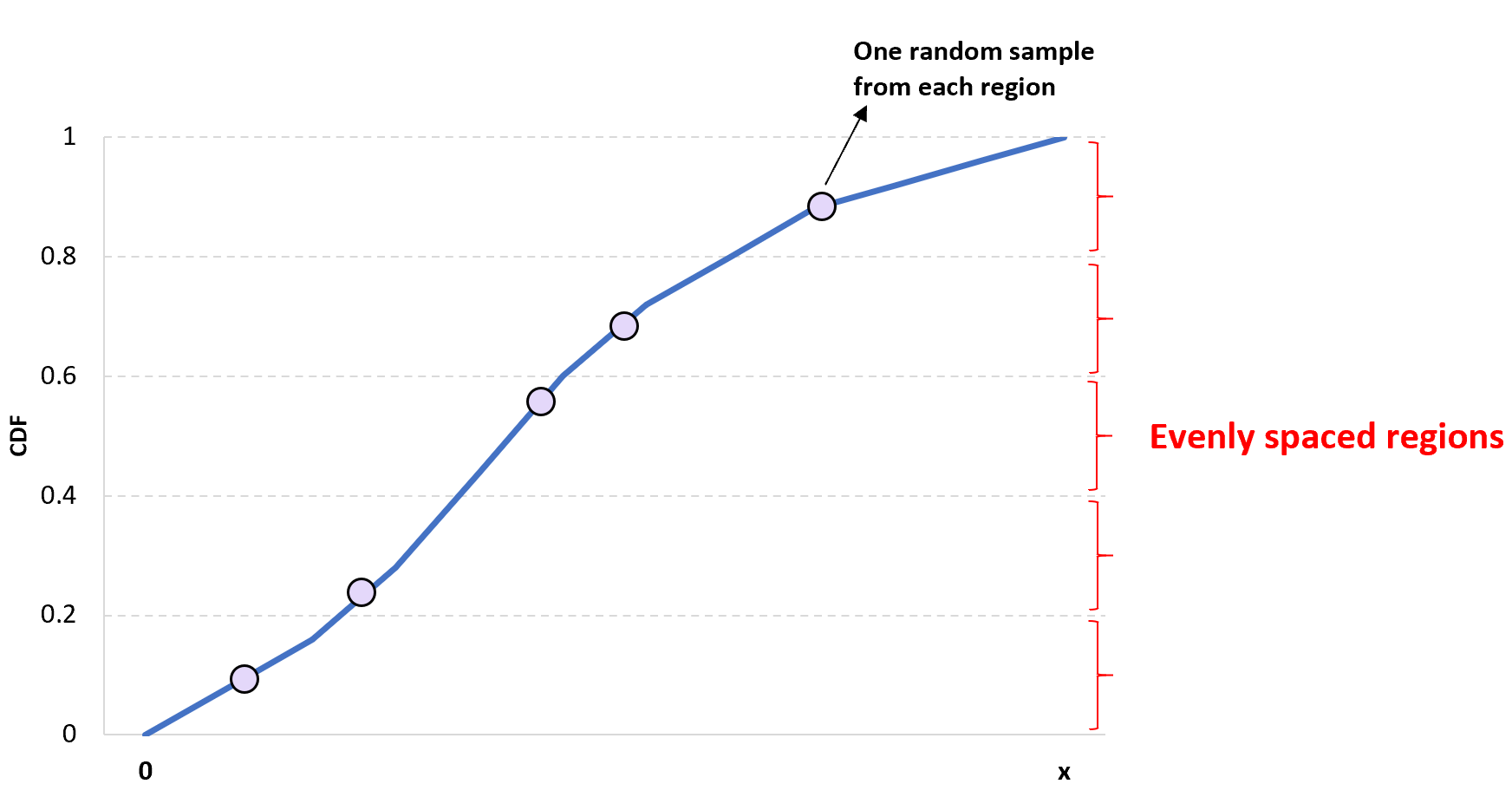
L’avantage de cette approche est qu’elle garantit qu’au moins une valeur de chaque région est incluse dans l’échantillon.
Échantillonnage d’hypercubes latins bidimensionnels
Nous pouvons facilement étendre l’idée de l’échantillonnage d’hypercube latin unidimensionnel à deux dimensions également.
Pour deux variables, x et y, nous pouvons diviser l’espace échantillon de chaque variable en n régions régulièrement espacées et sélectionner un échantillon aléatoire dans chaque espace échantillon pour obtenir des valeurs aléatoires sur deux dimensions.
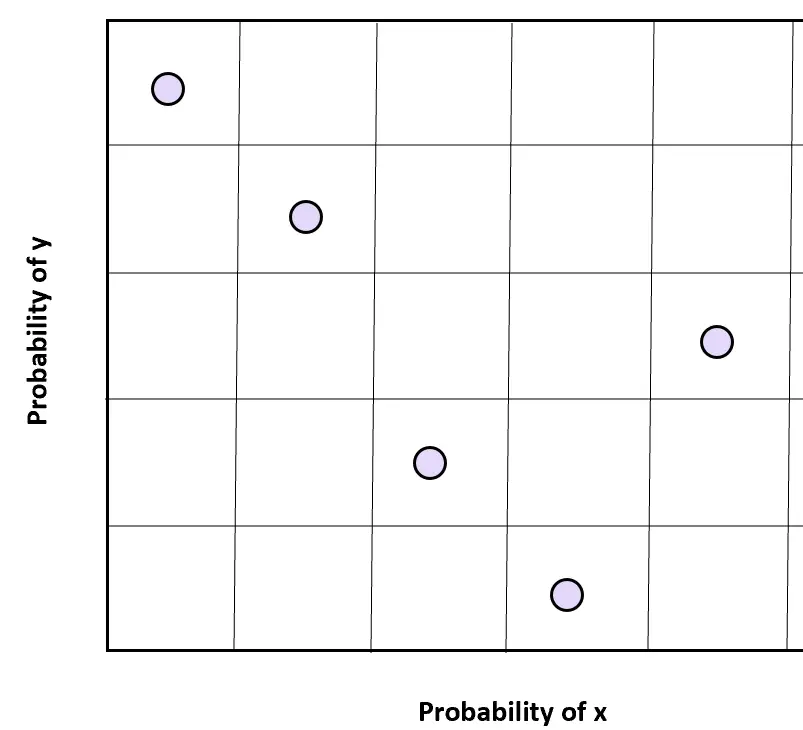
Il est important de noter que les deux variables doivent être indépendantes pour que cette technique d’échantillonnage obtienne les résultats souhaités.
Échantillonnage d’hypercube latin à N dimensions
Pour effectuer un échantillonnage d’hypercube latin dans de plus grandes dimensions, nous pouvons simplement étendre l’idée de l’échantillonnage d’hypercube latin bidimensionnel à encore plus de dimensions.
Chaque variable est simplement divisée en régions régulièrement espacées et des échantillons aléatoires sont ensuite choisis dans chaque région pour obtenir un échantillon aléatoire contrôlé.
Connexes : Qu’est-ce que les données de grande dimension ?
Pourquoi utiliser l’échantillonnage Latin Hypercube ?
Le principal avantage de l’échantillonnage hypercube latin est qu’il produit des échantillons qui reflètent la véritable distribution sous-jacente et qu’il a tendance à nécessiter des tailles d’échantillon beaucoup plus petites qu’un simple échantillonnage aléatoire .
Cette méthode d’échantillonnage peut être particulièrement avantageuse si vous travaillez avec des données comportant un nombre élevé de dimensions et que vous devez obtenir des échantillons aléatoires qui sont sûrs de refléter la véritable distribution sous-jacente des données.
