Comprendre la forme d’une distribution binomiale

La distribution binomiale décrit la probabilité d’obtenir k succès dans n expériences binomiales.

Si une variable aléatoire X suit une distribution binomiale, alors la probabilité que X = k succès peut être trouvée par la formule suivante :

P(X=k) = _n C _k * p ^k * (1-p) ^nk

où:

• n : nombre d’essais
• k : nombre de réussites
• p : probabilité de succès sur un essai donné
• _n C _k : le nombre de façons d’obtenir k succès dans n essais

La distribution de probabilité binomiale a tendance à être en forme de cloche lorsqu’une ou plusieurs des deux conditions suivantes se produisent :

1. La taille de l’échantillon (n) est grande.

2. La probabilité de réussite d’un essai donné (p) est proche de 0,5.

Cependant, la distribution de probabilité binomiale a tendance à être asymétrique lorsqu’aucune de ces conditions ne se produit. Pour illustrer cela, considérons les exemples suivants :

Exemple 1 : la taille de l’échantillon (n) est grande

Le graphique suivant affiche la distribution de probabilité lorsque n = 200 et p = 0,5 .

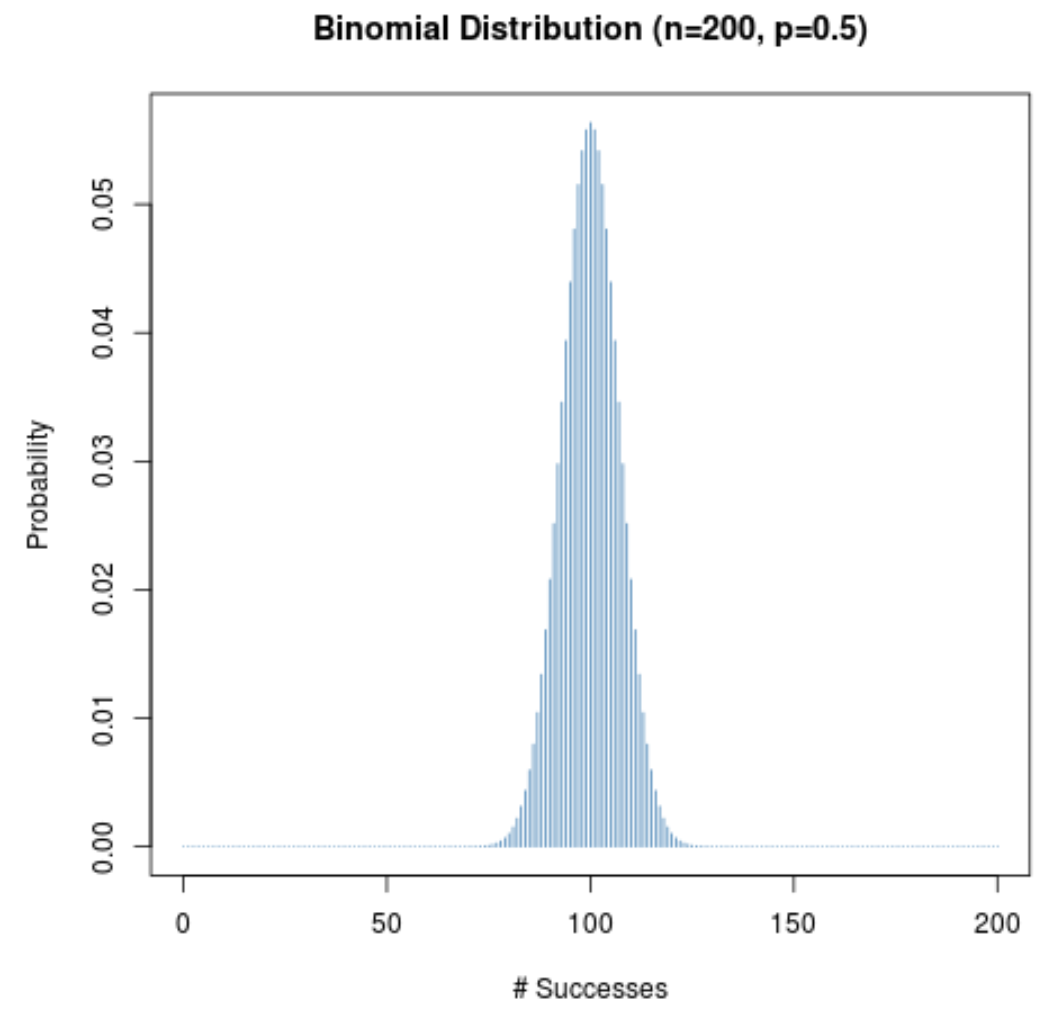
L’axe des x affiche le nombre de réussites au cours de 200 essais et l’axe des y affiche la probabilité que ce nombre de réussites se produise.

Étant donné que (1) la taille de l’échantillon est grande et (2) la probabilité de succès d’un essai donné est proche de 0,5, la distribution de probabilité est en forme de cloche.

Même lorsque la probabilité de succès d’un essai donné (p) n’est pas proche de 0,5, la distribution de probabilité restera en forme de cloche tant que la taille de l’échantillon (n) est grande. Pour illustrer cela, considérons les deux scénarios suivants lorsque p = 0,2 et p = 0,8.

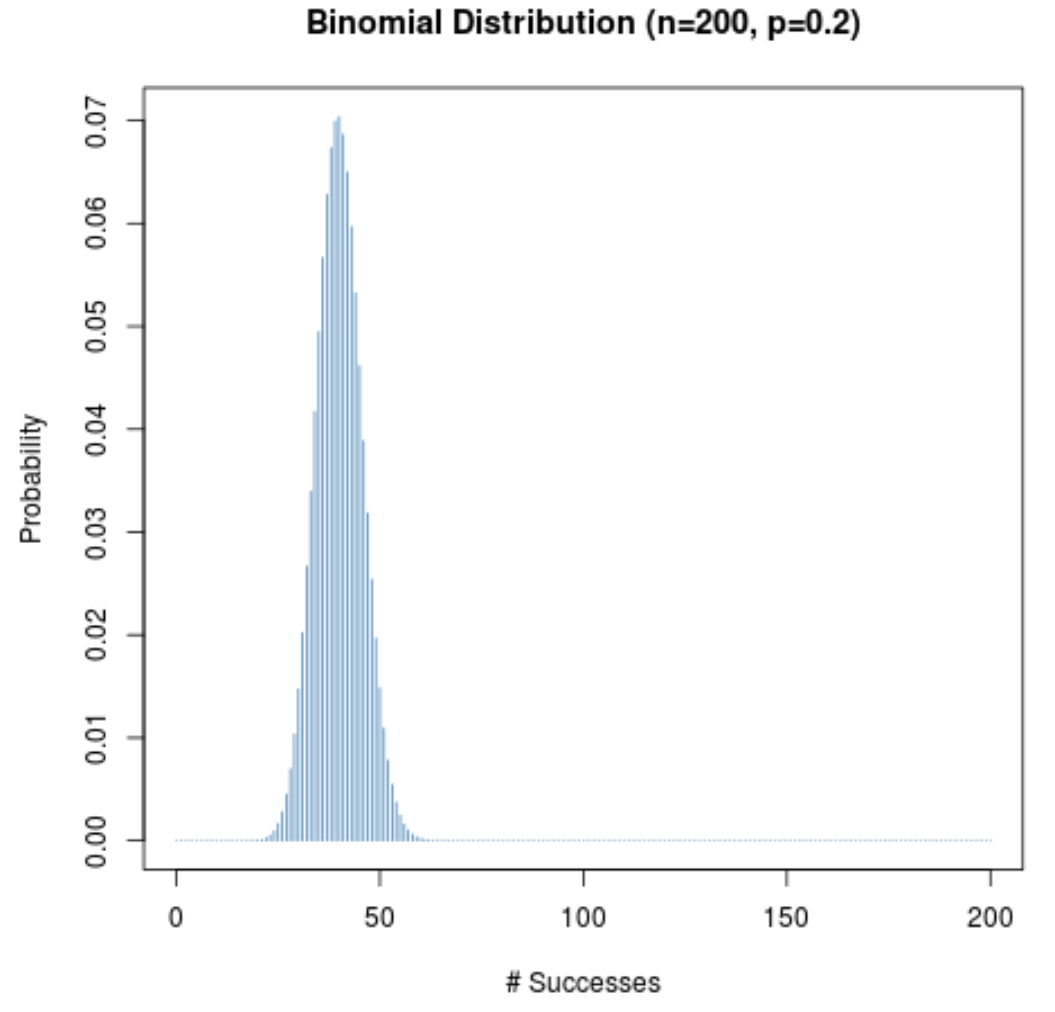
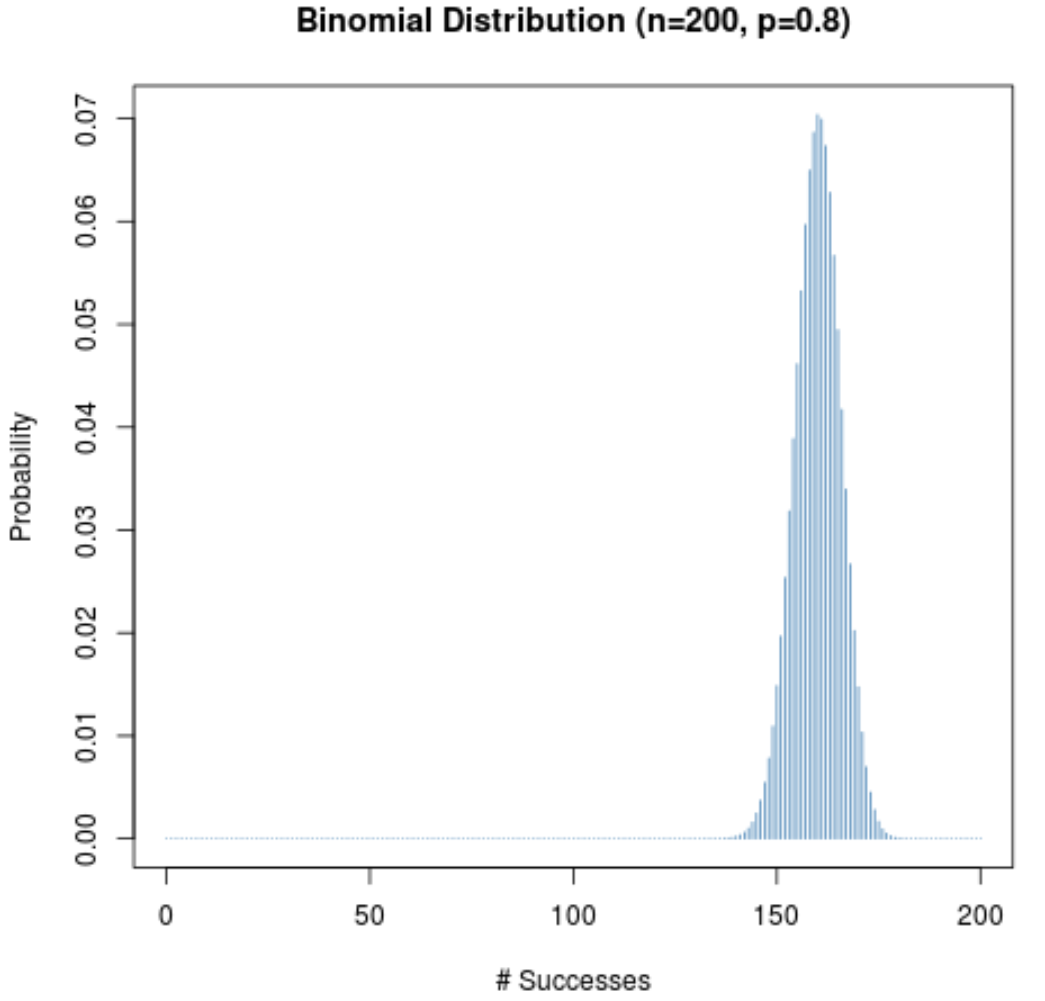
Remarquez comment la distribution de probabilité est en forme de cloche dans les deux scénarios.

Exemple 2 : la probabilité de succès (p) est proche de 0,5

Le graphique suivant affiche la distribution de probabilité lorsque n = 10 et p = 0,4 .

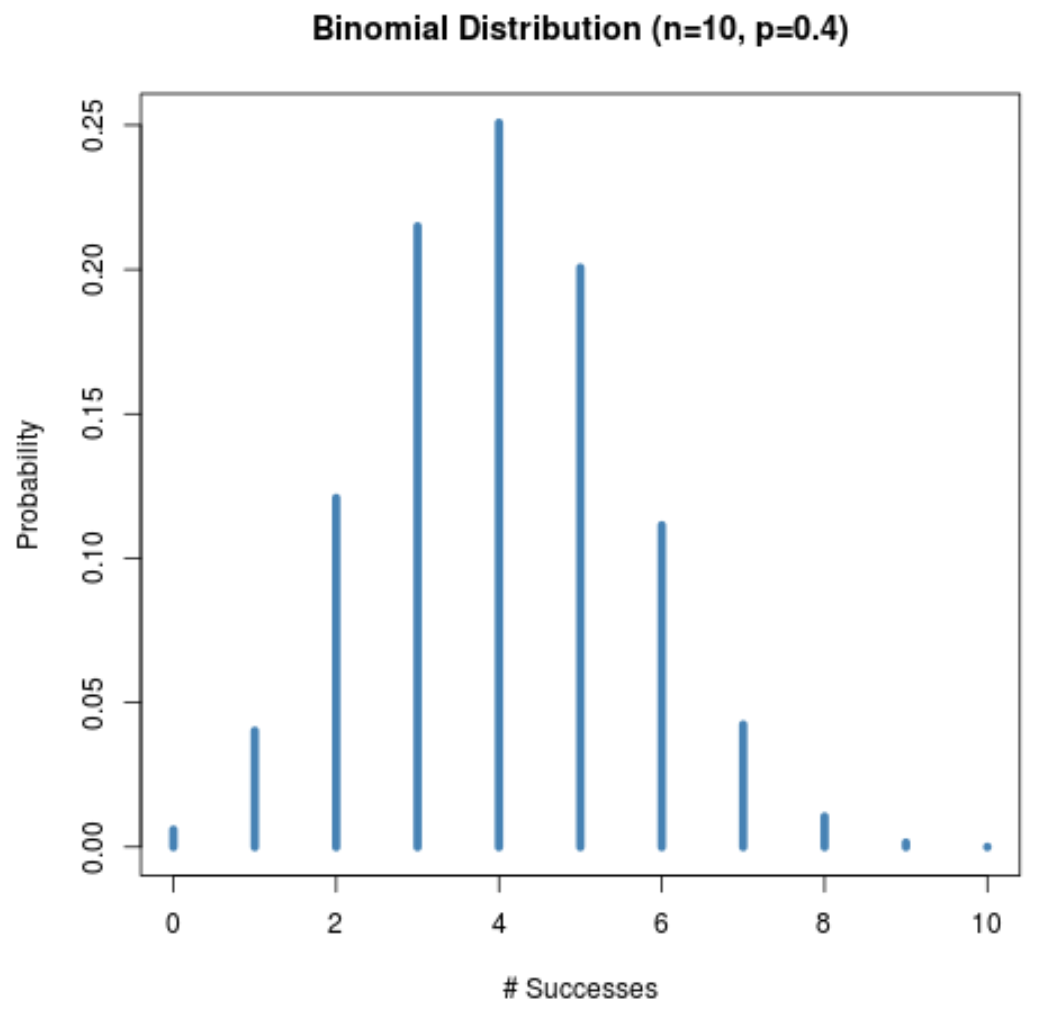
Bien que la taille de l’échantillon (n = 10) soit petite, la distribution de probabilité reste en forme de cloche car la probabilité de réussite d’un essai donné (p = 0,4) est proche de 0,5.

Exemple 3 : Distributions binomiales asymétriques

Lorsque ni (1) la taille de l’échantillon n’est grande ni (2) la probabilité de succès d’un essai donné n’est proche de 0,5, la distribution de probabilité binomiale sera asymétrique vers la gauche ou la droite.

Par exemple, le graphique suivant montre la distribution de probabilité lorsque n = 20 et p = 0,1 .

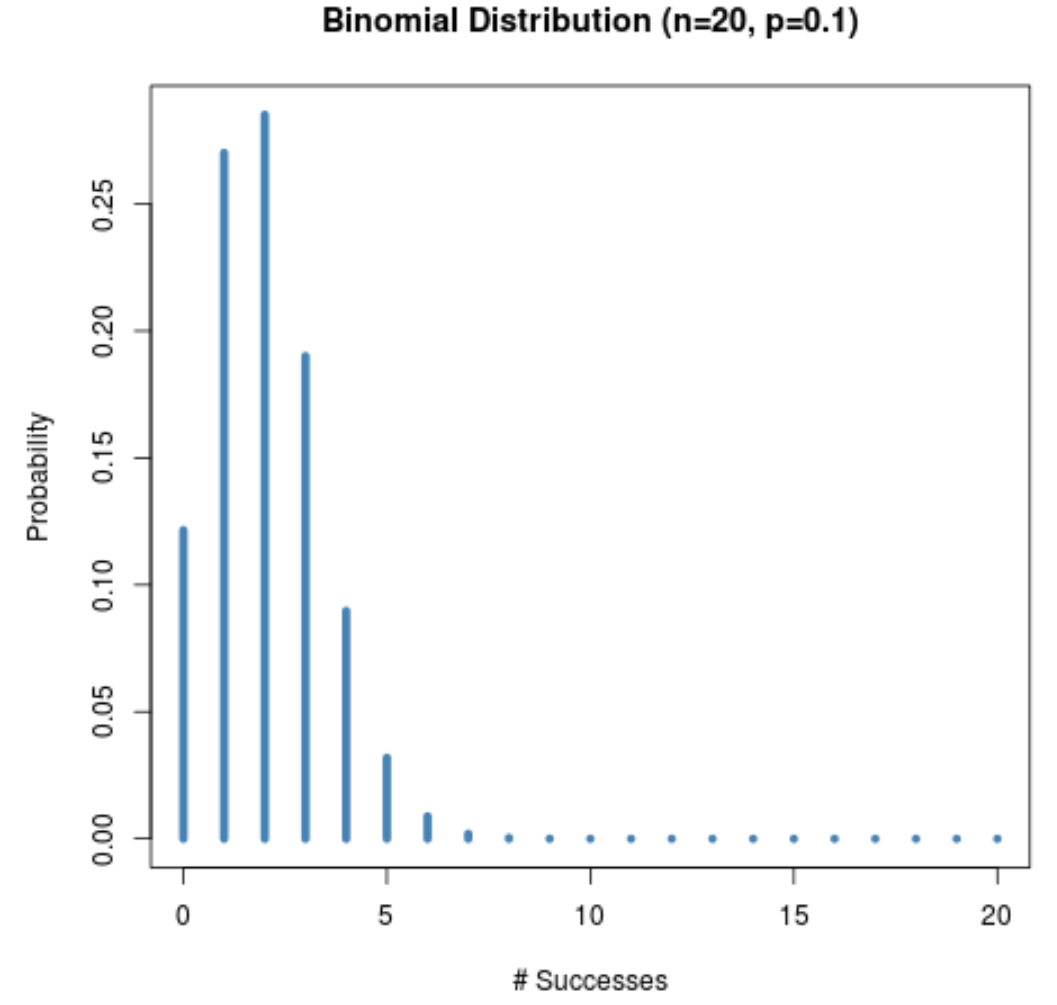
Remarquez comment la distribution est asymétrique vers la droite.

Et le graphique suivant montre la distribution de probabilité lorsque n = 20 et p = 0,9 .

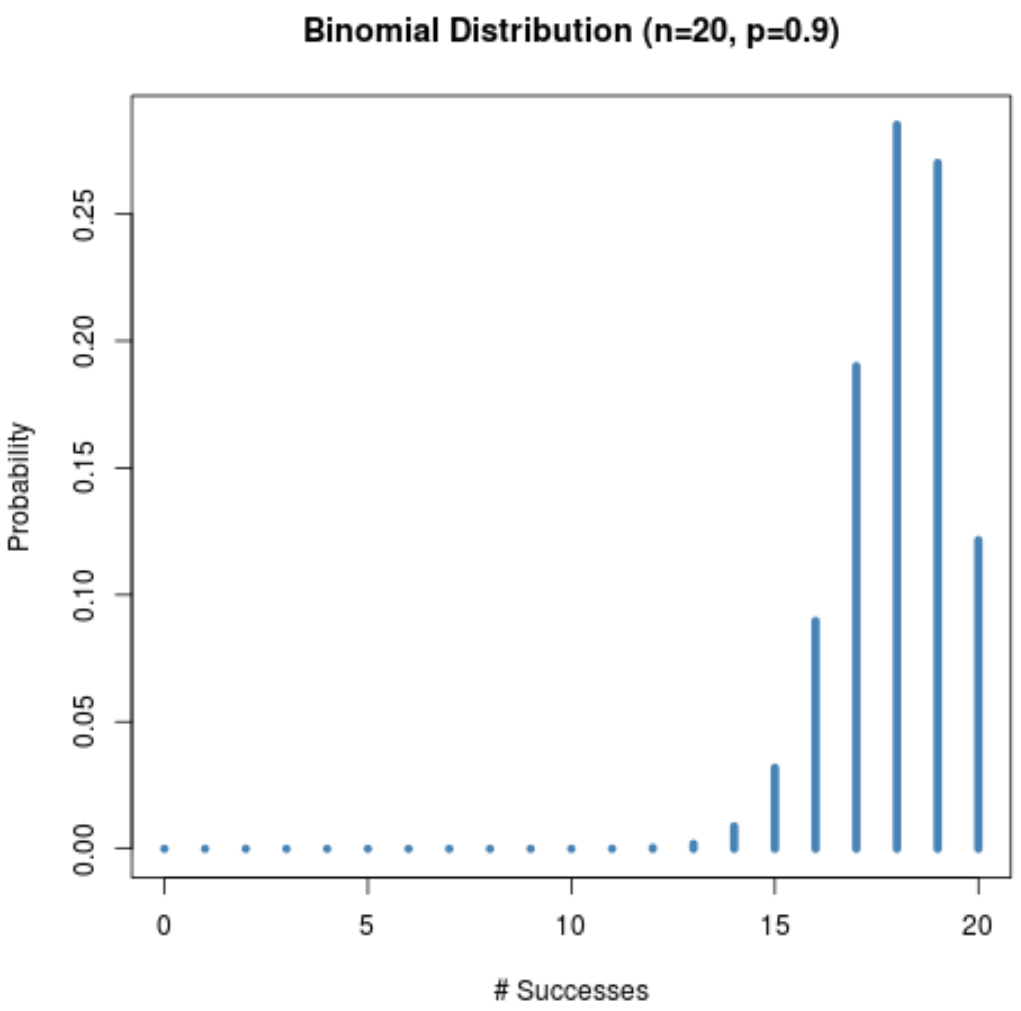
Remarquez comment la distribution est asymétrique vers la gauche.

Notes de fin

Chacun des graphiques de cet article a été créé à l’aide du langage de programmation statistique R. Apprenez à tracer vos propres distributions de probabilité binomiale dans R à l’aide de ce didacticiel .