Écart type et erreur type : quelle est la différence ?

Deux termes que les étudiants confondent souvent en statistiques sont l’écart type et l’erreur type .

L’ écart type mesure la répartition des valeurs dans un ensemble de données.

L’ erreur type est l’écart type de la moyenne d’échantillons répétés d’une population.

Voyons un exemple pour illustrer clairement cette idée.

Exemple : écart type par rapport à l’erreur type

Supposons que nous mesurions le poids de 10 tortues différentes.

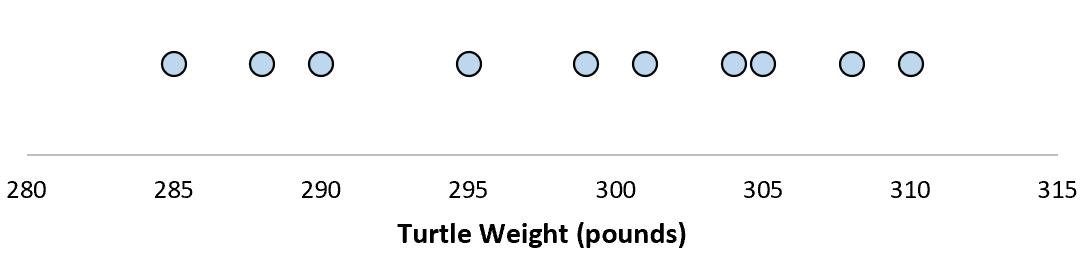
Pour cet échantillon de 10 tortues, nous pouvons calculer la moyenne de l’échantillon et l’écart type de l’échantillon :

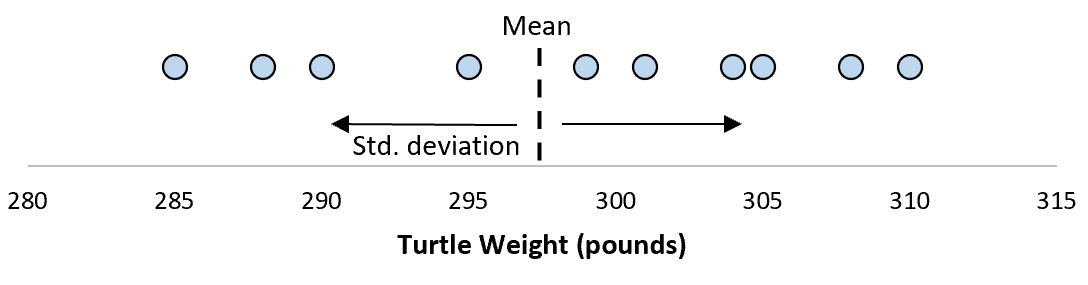
Supposons que l’écart type soit de 8,68. Cela nous donne une idée de la répartition des poids de ces tortues.

Mais supposons que nous collections un autre échantillon aléatoire simple de 10 tortues et que nous prenions également leurs mesures.

Il est plus que probable que cet échantillon de 10 tortues aura une moyenne et un écart type légèrement différents, même si elles proviennent de la même population :

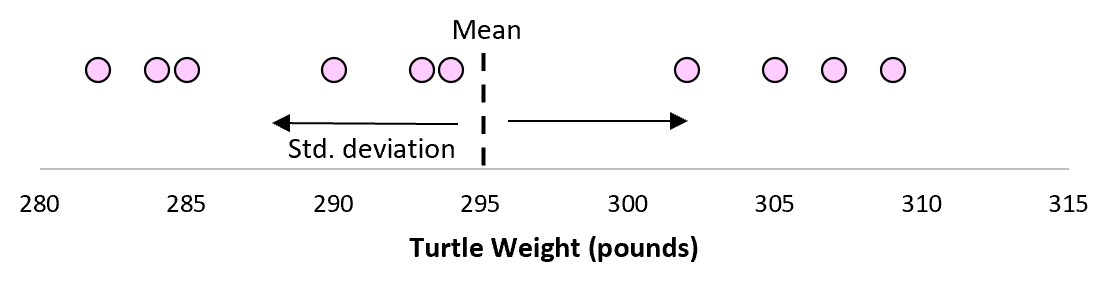
Maintenant, si nous imaginons que nous prenons des échantillons répétés de la même population et enregistrons la moyenne de l’échantillon et l’écart type de l’échantillon pour chaque échantillon :

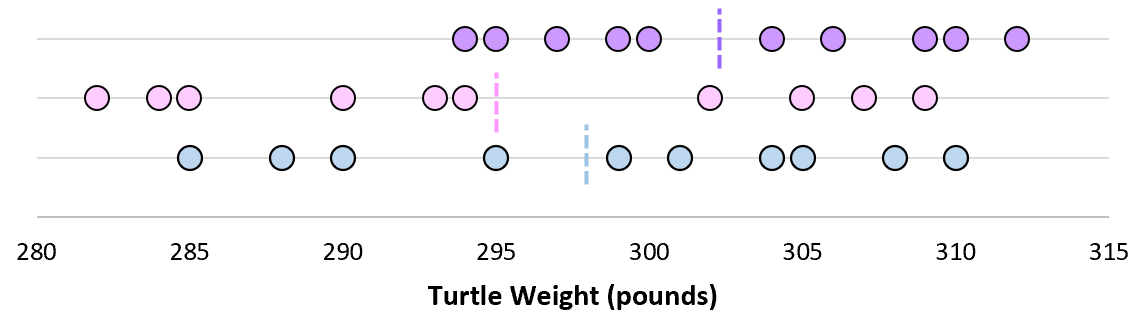
Imaginez maintenant que nous traçons chacune des moyennes de l’échantillon sur la même ligne :

L’écart type de ces moyennes est appelé erreur type.

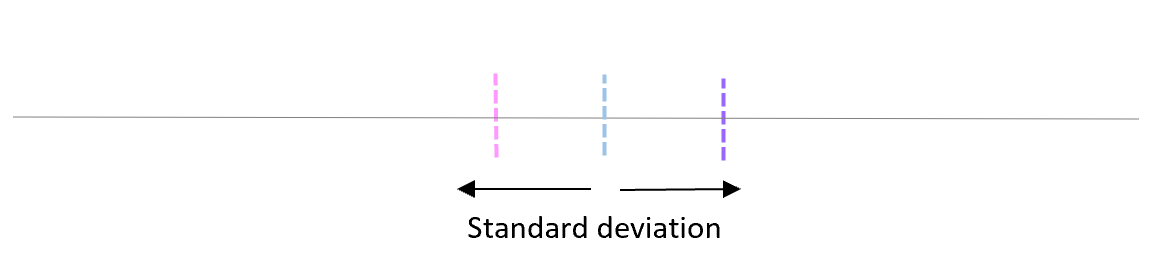
La formule pour calculer réellement l’erreur type est la suivante :

Erreur standard = s/ √ n

où:

• s : écart type de l’échantillon
• n : taille de l’échantillon

Quel est l’intérêt d’utiliser l’erreur standard ?

Lorsque nous calculons la moyenne d’un échantillon donné, nous ne cherchons pas réellement à connaître la moyenne de cet échantillon particulier, mais plutôt la moyenne de la population plus large dont provient l’échantillon.

Cependant, nous utilisons des échantillons car il est beaucoup plus facile de collecter des données pour eux que pour une population entière.

Et bien sûr, la moyenne de l’échantillon varie d’un échantillon à l’autre, nous utilisons donc l’ erreur standard de la moyenne comme moyen de mesurer la précision de notre estimation de la moyenne.

Vous remarquerez dans la formule de calcul de l’erreur standard qu’à mesure que la taille de l’échantillon (n) augmente, l’erreur standard diminue :

Erreur standard = s/ √ n

Cela devrait avoir du sens, car des échantillons plus grands réduisent la variabilité et augmentent les chances que la moyenne de notre échantillon soit plus proche de la moyenne réelle de la population.

Quand utiliser l’écart type par rapport à l’erreur standard

Si nous souhaitons simplement mesurer la répartition des valeurs dans un ensemble de données, nous pouvons utiliser l’ écart type .

Cependant, si nous souhaitons quantifier l’incertitude autour d’une estimation de la moyenne, nous pouvons utiliser l’ erreur standard de la moyenne .

En fonction de votre scénario spécifique et de ce que vous essayez d’accomplir, vous pouvez choisir d’utiliser l’écart type ou l’erreur type.