Comment effectuer un test post hoc Tukey-Kramer dans Excel
Une ANOVA unidirectionnelle est utilisée pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes indépendants ou plus.
Les hypothèses utilisées dans une ANOVA sont les suivantes :
L’hypothèse nulle (H 0 ) : µ 1 = µ 2 = µ 3 = … = µ k (les moyennes sont égales pour chaque groupe)
L’hypothèse alternative : (Ha) : au moins une des moyennes est différente des autres
Si la valeur p de l’ANOVA est inférieure au niveau de signification, nous pouvons rejeter l’hypothèse nulle et conclure que nous disposons de preuves suffisantes pour dire qu’au moins une des moyennes des groupes est différente des autres.
Cependant, cela ne nous dit pas quels groupes sont différents les uns des autres. Cela nous dit simplement que toutes les moyennes du groupe ne sont pas égales. Afin de savoir exactement quels groupes sont différents les uns des autres, nous devons effectuer un test post hoc.
Le test post hoc le plus couramment utilisé est le test de Tukey-Kramer , qui compare la moyenne entre chaque combinaison de groupes par paire.
L’exemple suivant montre comment effectuer le test Tukey-Kramer dans Excel.
Exemple : test de Tukey-Kramer dans Excel
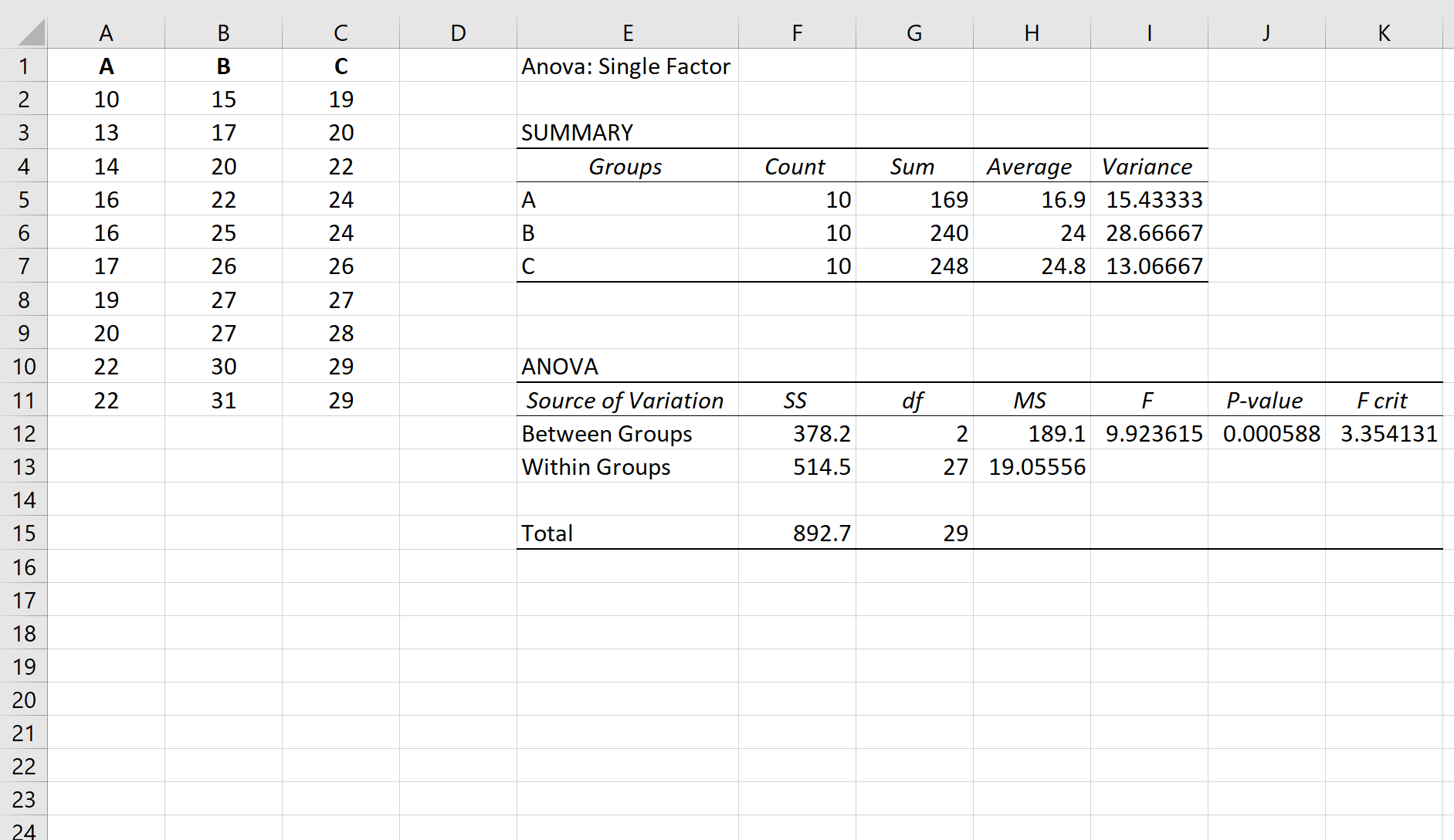
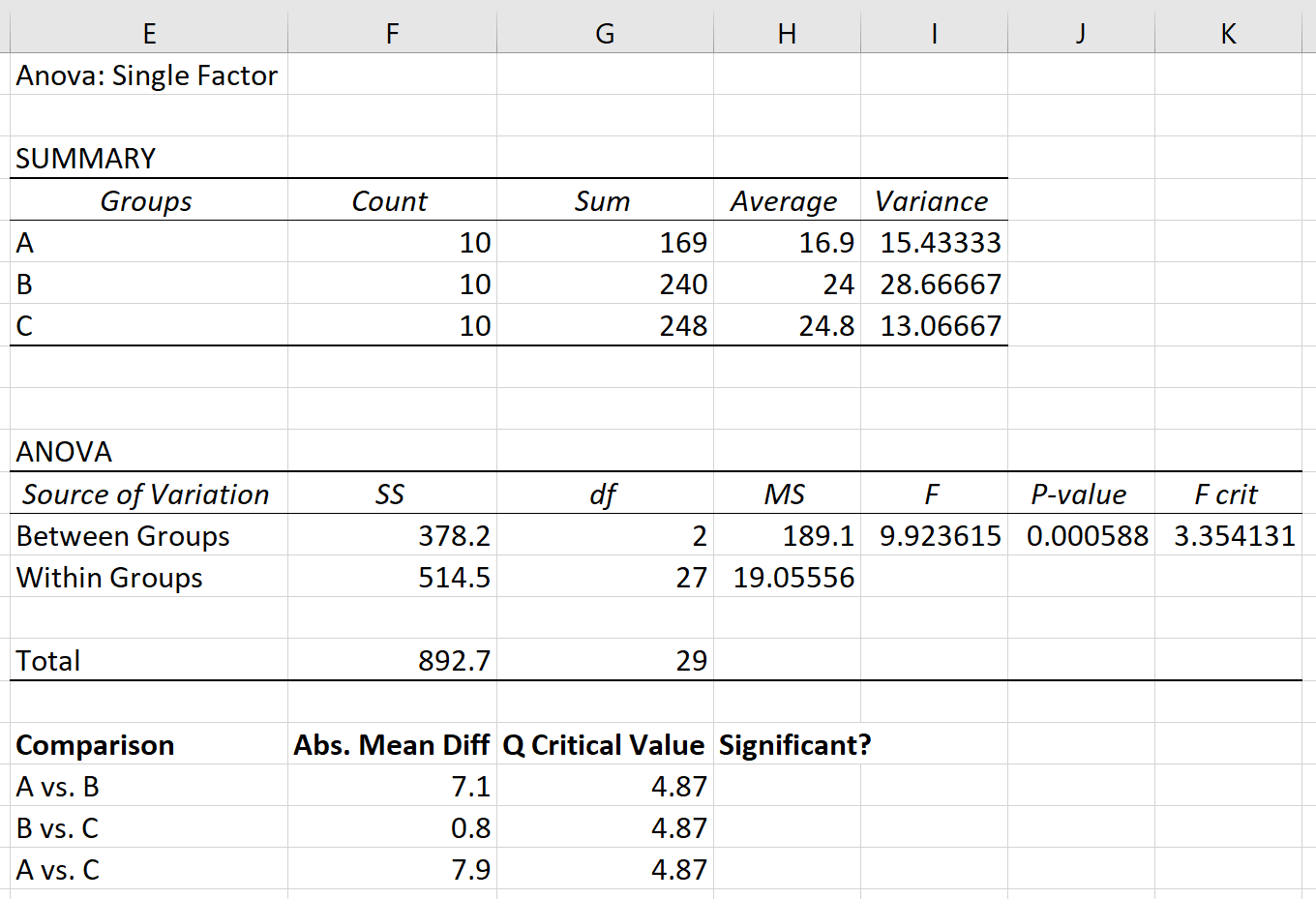
Supposons que nous effectuions une ANOVA unidirectionnelle sur trois groupes : A, B et C. Les résultats de l’ANOVA unidirectionnelle sont présentés ci-dessous :
Connexe : Comment effectuer une ANOVA unidirectionnelle dans Excel
La valeur p du tableau ANOVA est 0,000588 . Puisque cette valeur p est inférieure à 0,05, nous pouvons rejeter l’hypothèse nulle et conclure que les moyennes entre les trois groupes ne sont pas égales.
Pour déterminer exactement quelles moyennes de groupe sont différentes, nous pouvons effectuer un test post hoc de Tukey-Kramer en suivant les étapes suivantes :
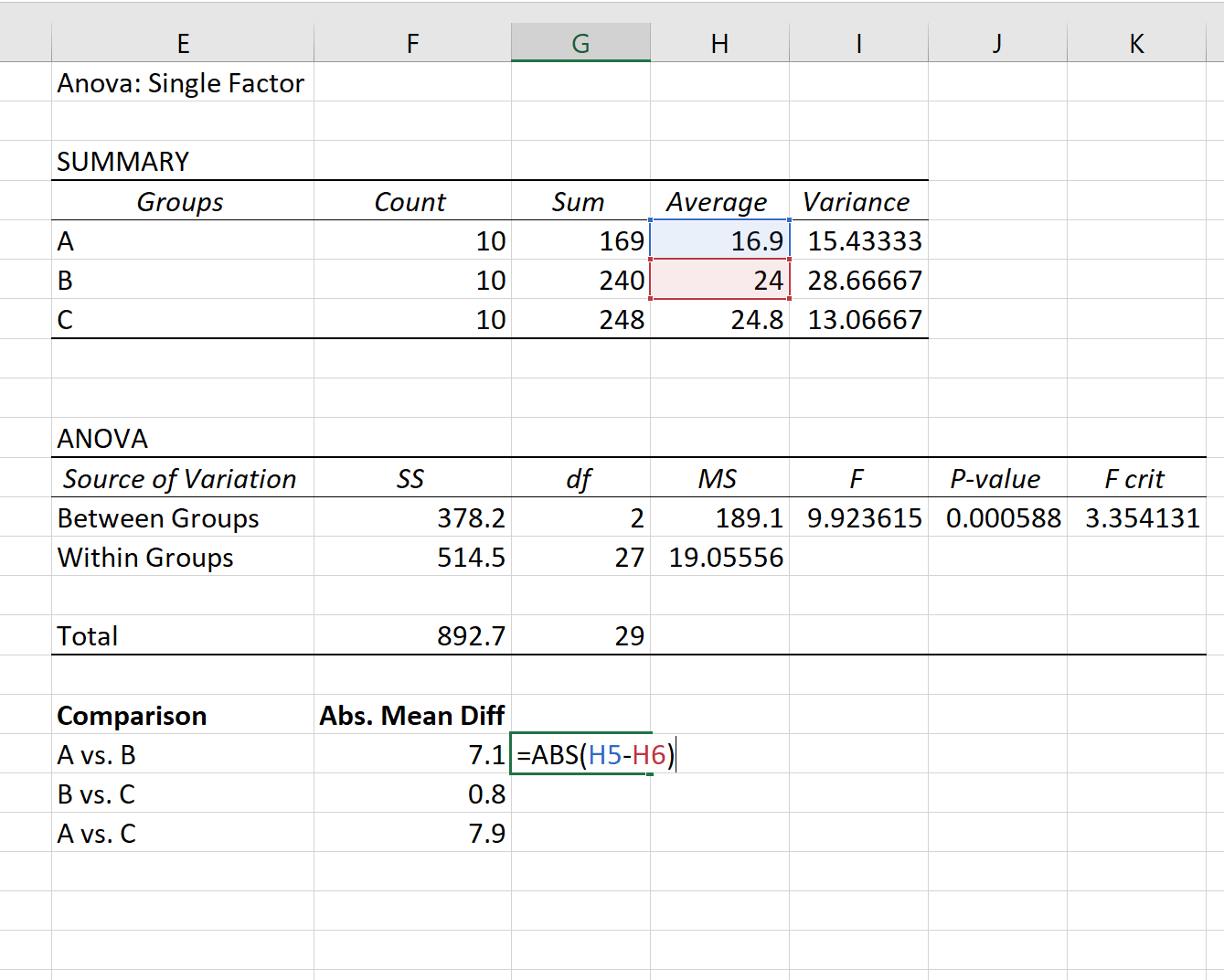
Étape 1 : Trouvez la différence moyenne absolue entre chaque groupe.
Tout d’abord, nous trouverons la différence moyenne absolue entre chaque groupe en utilisant les moyennes répertoriées dans le premier tableau du résultat ANOVA :
Étape 2 : Trouvez la valeur critique de Q.
Ensuite, nous devons trouver la valeur critique de Q en utilisant la formule suivante :
Valeur critique Q = Q*√(s 2 regroupés / n.)
où:
- Q = Valeur de la plage de Student Tableau Q
- s 2 regroupé = variance regroupée dans tous les groupes
- n. = Taille de l’échantillon pour un groupe donné
Pour trouver la valeur Q, vous pouvez vous référer au tableau Q de plage Studentized qui ressemble à ceci :
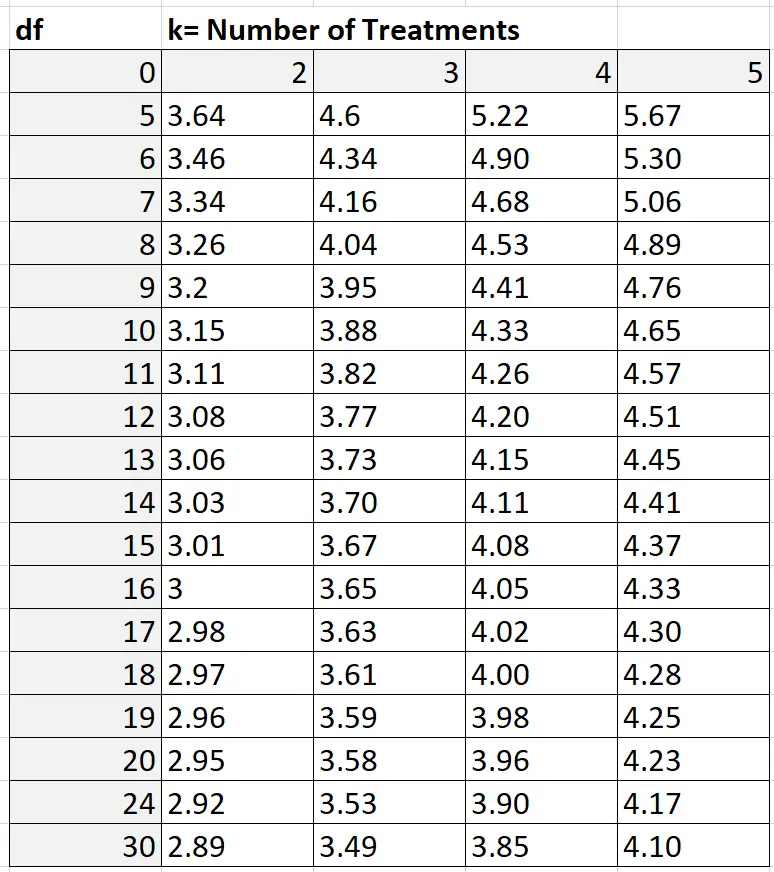
Dans notre exemple, k = le nombre de groupes, soit k = 3. Les degrés de liberté sont calculés comme suit : nk = 30 – 3 = 27. Puisque 27 n’est pas indiqué dans le tableau ci-dessus, nous pouvons utiliser une estimation prudente de 24. En fonction de k = 3 et df = 24, nous trouvons que Q = 3,53 .
La variance groupée peut être calculée comme la moyenne des variances des groupes, ce qui s’avère être 19,056 .
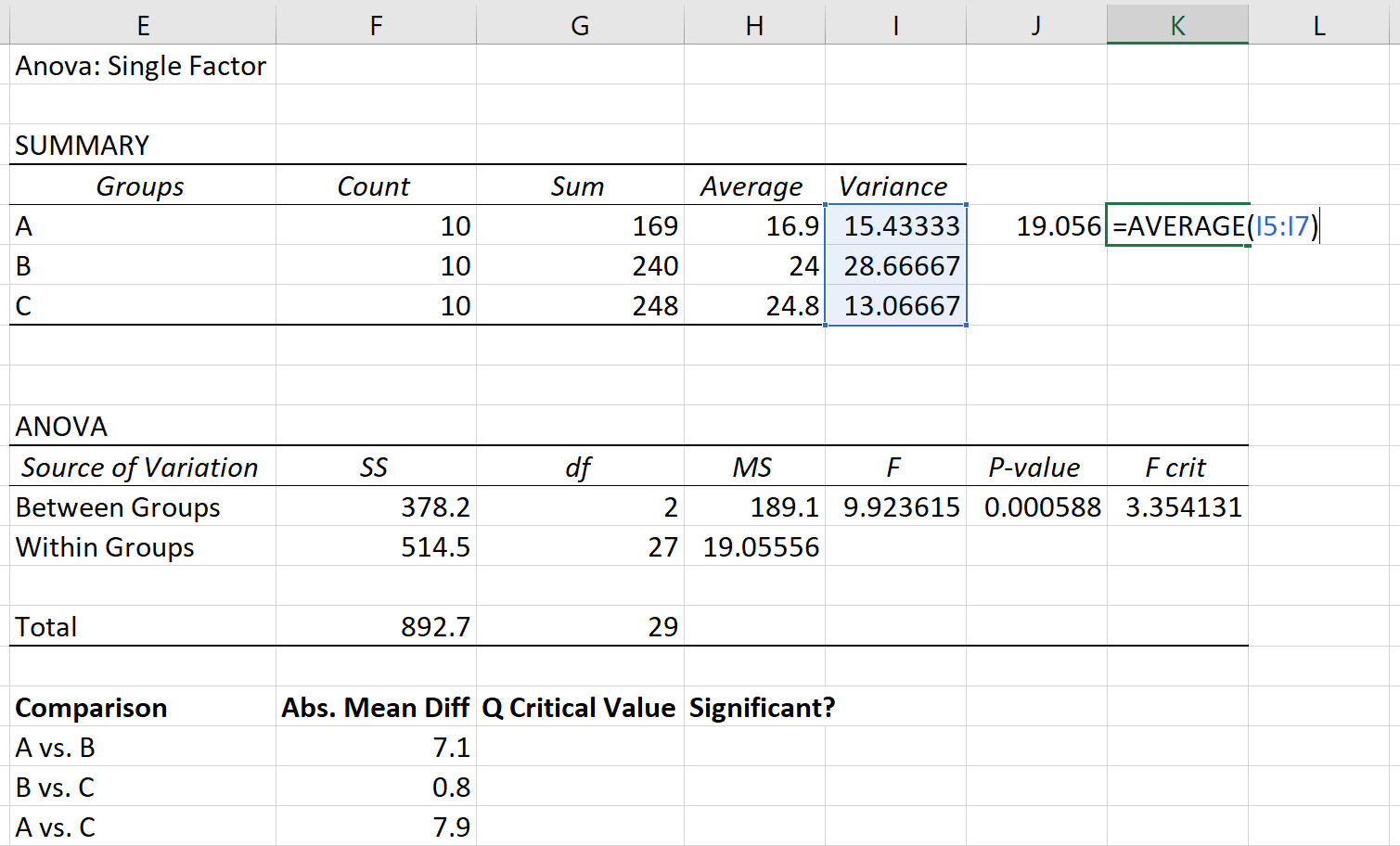
Enfin, la taille de l’échantillon de chaque groupe est de 10.
Ainsi, notre valeur critique Q peut être calculée comme suit :
Valeur critique Q = Q*√(s 2 regroupés / n.) = 3,53*√(19,056/10) = 4,87 .
Étape 3 : Déterminez quelles moyennes de groupe sont différentes .
Enfin, nous pouvons comparer la différence moyenne absolue entre chaque groupe à la valeur critique Q. Si la différence moyenne absolue est supérieure à la valeur critique Q, alors la différence entre les moyennes des groupes est statistiquement significative :
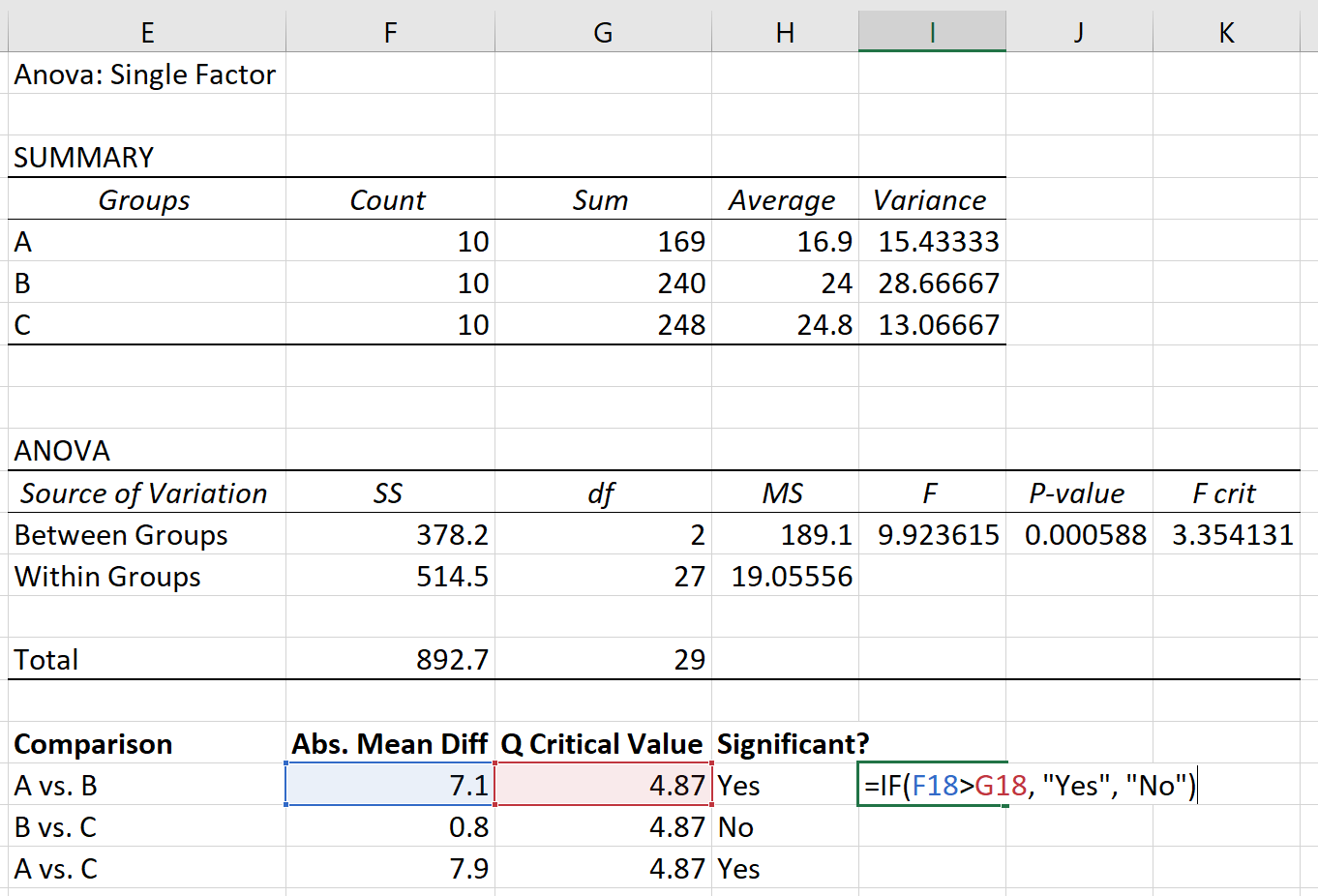
Sur la base du test post hoc de Tukey-Kramer, nous avons constaté ce qui suit :
- La différence de moyenne entre le groupe A et le groupe B est statistiquement significative.
- La différence de moyenne entre le groupe B et le groupe C n’est pas statistiquement significative.
- La différence de moyenne entre le groupe A et le groupe C est statistiquement significative.
Ressources additionnelles
Comment effectuer une ANOVA unidirectionnelle dans Excel
Un guide d’utilisation des tests post-hoc avec ANOVA
