Loi des grands nombres : définition + exemples

La loi des grands nombres stipule qu’à mesure que la taille d’un échantillon augmente, la moyenne de l’échantillon se rapproche de la valeur attendue.

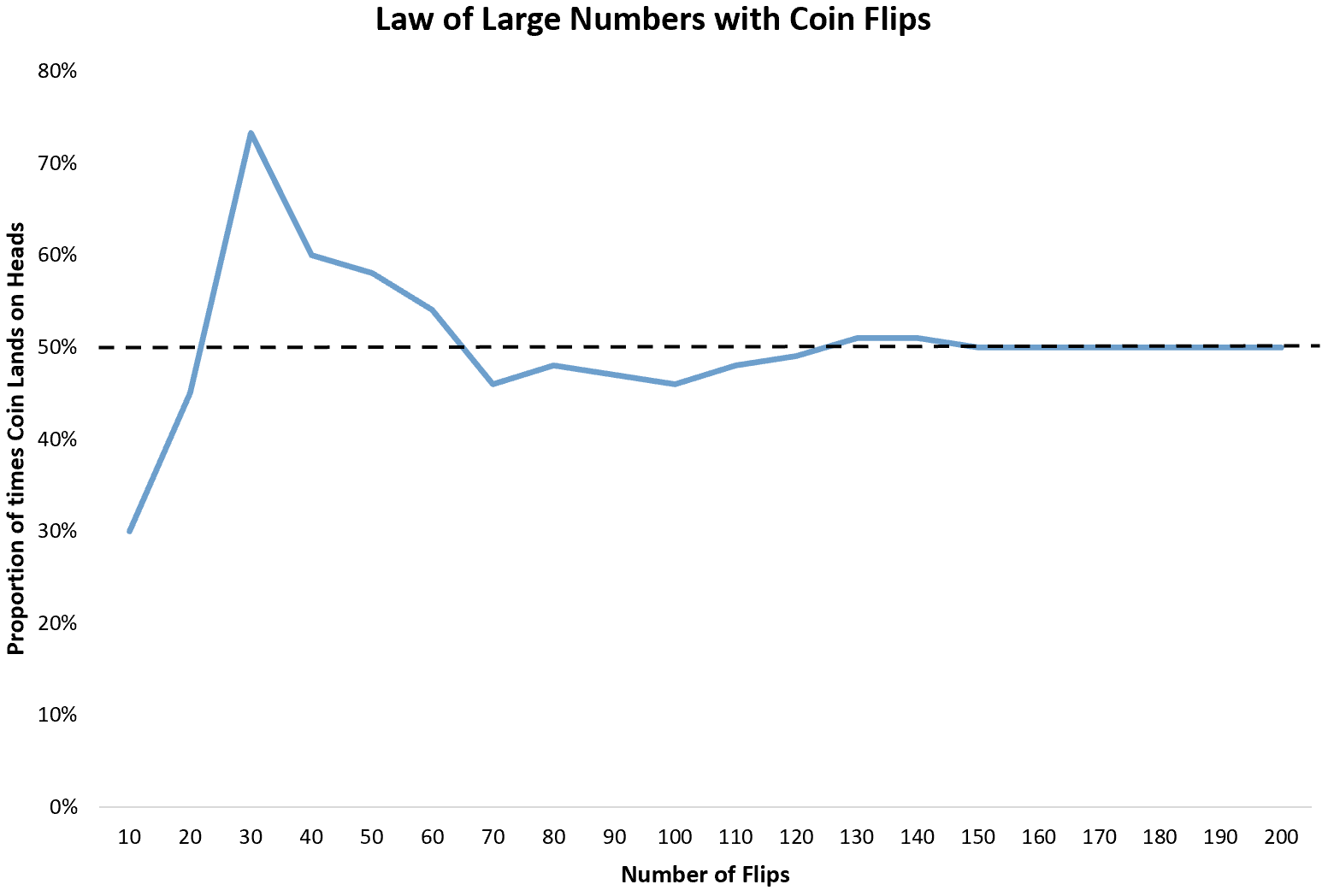
L’exemple le plus élémentaire consiste à lancer une pièce de monnaie. Chaque fois que nous lançons une pièce, la probabilité qu’elle tombe sur face est de 1/2. Ainsi, la proportion attendue de têtes qui apparaîtront sur un nombre infini de lancers est de 1/2 ou 0,5 .

Cependant, si nous lançons une pièce 10 fois, nous pourrions constater qu’elle n’atteint que 3 fois sur face. Étant donné que 10 flips représentent une petite taille d’échantillon, rien ne garantit que la proportion de têtes sera proche de 0,5 .

Si nous continuons à lancer la pièce encore 10 fois, nous pourrions constater qu’elle atterrit sur face un total de 9 fois sur 20. Si nous la lançons encore 10 fois, nous pourrions constater qu’elle atterrit sur face 22 fois sur 30.

Au fur et à mesure que nous lançons la pièce, la proportion de fois où elle tombe sur face convergera vers la proportion attendue de 0,5 .

Cette idée simple de la loi des grands nombres est appliquée par de nombreux types d’entreprises et d’industries dans la vie réelle.

La loi des grands nombres dans les casinos

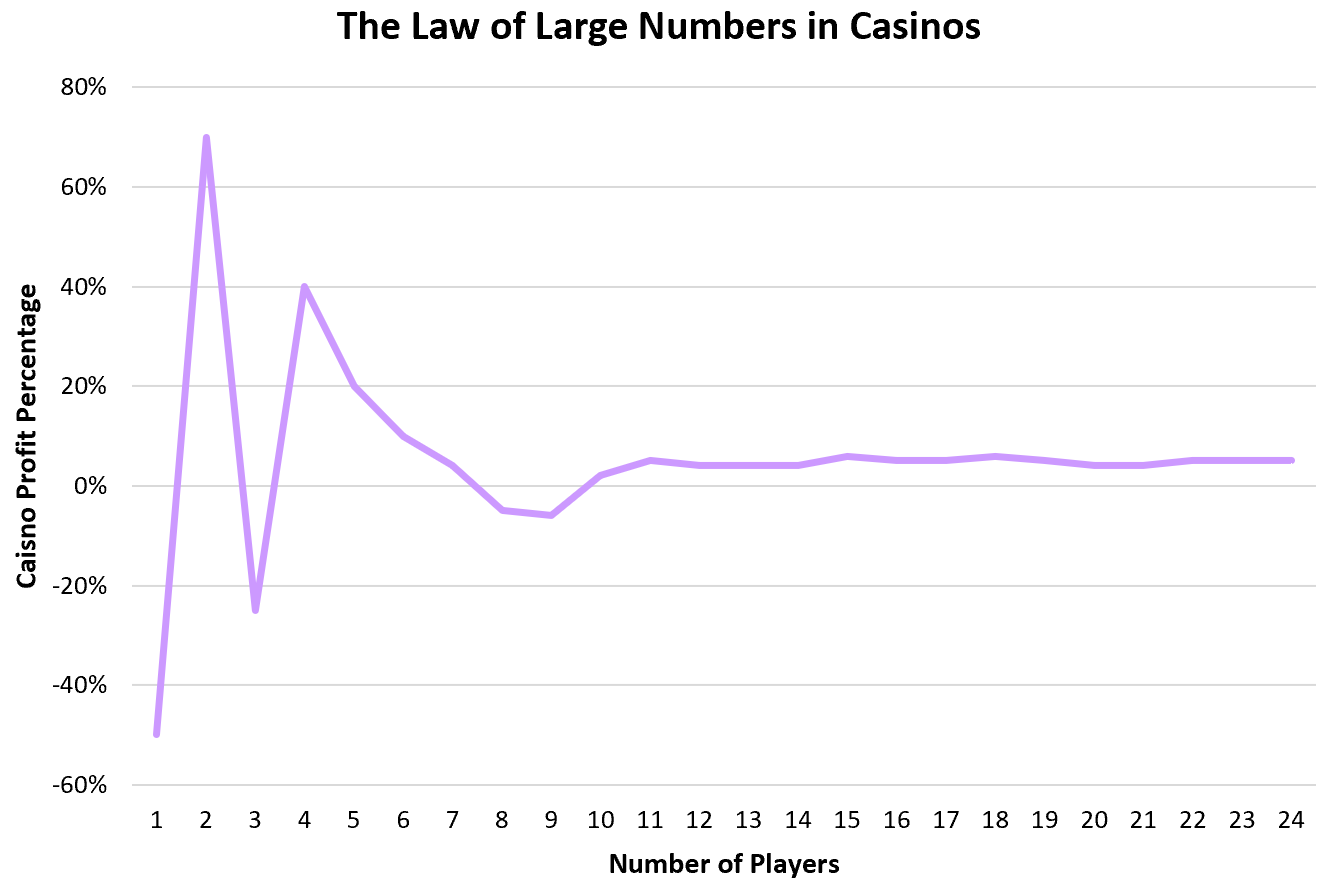
Les casinos s’appuient sur la loi des grands nombres pour générer des bénéfices de manière fiable. Pour la plupart des jeux, le casino gagne environ 51 à 55 % du temps. Cela signifie que les individus peuvent avoir de la chance et gagner un montant décent de temps en temps, mais sur des dizaines de milliers de joueurs individuels, le casino gagnera les 51 à 55 % du temps attendus.

Par exemple, Jessica pourrait jouer à quelques jeux au casino et gagner 50 $.

Mike pourrait également jouer à quelques jeux et perdre 70 $.

John pourrait jouer quelques jeux et gagner 25 $.

Susan pourrait jouer à quelques jeux et perdre 40 $.

Certains joueurs gagneront de l’argent et d’autres en perdront, mais grâce à la façon dont les jeux sont conçus, les casinos peuvent être sûrs qu’ils gagneront sur des milliers d’individus.

La loi des grands nombres en assurance

Les compagnies d’assurance s’appuient également sur la loi des grands nombres pour rester rentables.

L’idée de base est que les compagnies d’assurance peuvent fournir une assurance à des milliers de personnes qui paient une certaine prime chaque mois et que seul un petit pourcentage des personnes qu’elles assurent auront réellement besoin d’utiliser l’assurance pour payer d’importantes dépenses imprévues.

Par exemple, 1 000 personnes pourraient payer chacune 1 000 $ par an pour une assurance, ce qui générerait un bénéfice de 1 000 000 $ pour une compagnie d’assurance.

Cependant, 90 personnes pourraient avoir chacune besoin de recevoir 10 000 $ de la compagnie d’assurance pour couvrir les dépenses imprévues liées à divers accidents, ce qui entraînerait une perte de 900 000 $ pour la compagnie d’assurance.

Au final, la compagnie d’assurance réalise un bénéfice de 1 000 000 $ – 900 000 $ = 100 000 $ .

Cela signifie que la compagnie d’assurance peut s’attendre à réaliser un bénéfice assez prévisible, en moyenne, sur des milliers de personnes.

A noter que ce modèle économique fonctionne car une compagnie d’assurance assure un grand nombre de personnes . S’ils n’assuraient que 10 personnes, ce serait beaucoup trop risqué car une dépense imprévue importante pourrait anéantir l’entreprise.

Ainsi, les compagnies d’assurance s’appuient sur la loi des grands nombres pour prévoir leurs bénéfices de manière prévisible.

La loi des grands nombres dans les énergies renouvelables

La loi des grands nombres est également utilisée par les entreprises d’énergie renouvelable.

L’idée de base est que les éoliennes et les panneaux solaires peuvent alimenter des générateurs pour produire de l’électricité dans différentes parties de l’entreprise. Cependant, il n’y a ni vent ni soleil dehors, ce qui signifie que les éoliennes et les panneaux solaires ne sont pas toujours en mesure de produire une énergie fiable pour les générateurs électriques.

La façon dont les entreprises d’énergie renouvelable contournent ce problème consiste à connecter des dizaines de milliers d’éoliennes ou de panneaux solaires à un seul réseau électrique, ce qui rend beaucoup plus probable que ces sources d’énergie produiront une quantité fiable d’énergie pour le réseau.

Il est également beaucoup plus facile de prédire la quantité d’énergie qui sera produite par ces sources d’énergie, puisque les ingénieurs peuvent simplement prendre la moyenne attendue sur des dizaines de milliers d’éoliennes ou de panneaux solaires.

Une explication détaillée de ce phénomène peut être trouvée dans cet article de Scientific American .