Comment créer un tracé résiduel en Python
Un tracé des résidus est un type de tracé qui affiche les valeurs ajustées par rapport aux valeurs résiduelles d’un modèle de régression .
Ce type de graphique est souvent utilisé pour évaluer si un modèle de régression linéaire est approprié ou non pour un ensemble de données donné et pour vérifier l’hétéroscédasticité des résidus.
Ce didacticiel explique comment créer un tracé résiduel pour un modèle de régression linéaire en Python.
Exemple : tracé résiduel en Python
Pour cet exemple, nous utiliserons un ensemble de données qui décrit les attributs de 10 joueurs de basket-ball :
import numpy as np import pandas as pd #create dataset df = pd.DataFrame({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86], 'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19], 'assists': [5, 7, 7, 8, 5, 7, 6, 9, 9, 5], 'rebounds': [11, 8, 10, 6, 6, 9, 6, 10, 10, 7]}) #view dataset df rating points assists rebounds 0 90 25 5 11 1 85 20 7 8 2 82 14 7 10 3 88 16 8 6 4 94 27 5 6 5 90 20 7 9 6 76 12 6 6 7 75 15 9 10 8 87 14 9 10 9 86 19 5 7
Tracé résiduel pour une régression linéaire simple
Supposons que nous ajustions un modèle de régression linéaire simple en utilisant des points comme variable prédictive et une note comme variable de réponse :
#import necessary libraries import matplotlib.pyplot as plt import statsmodels.api as sm from statsmodels.formula.api import ols #fit simple linear regression model model = ols('rating ~ points', data=df).fit() #view model summary print(model.summary())
Nous pouvons créer un tracé résiduel ou ajusté en utilisant la fonction plot_regress_exog() de la bibliothèque statsmodels :
#define figure size fig = plt.figure(figsize=(12,8)) #produce regression plots fig = sm.graphics.plot_regress_exog(model, 'points', fig=fig)
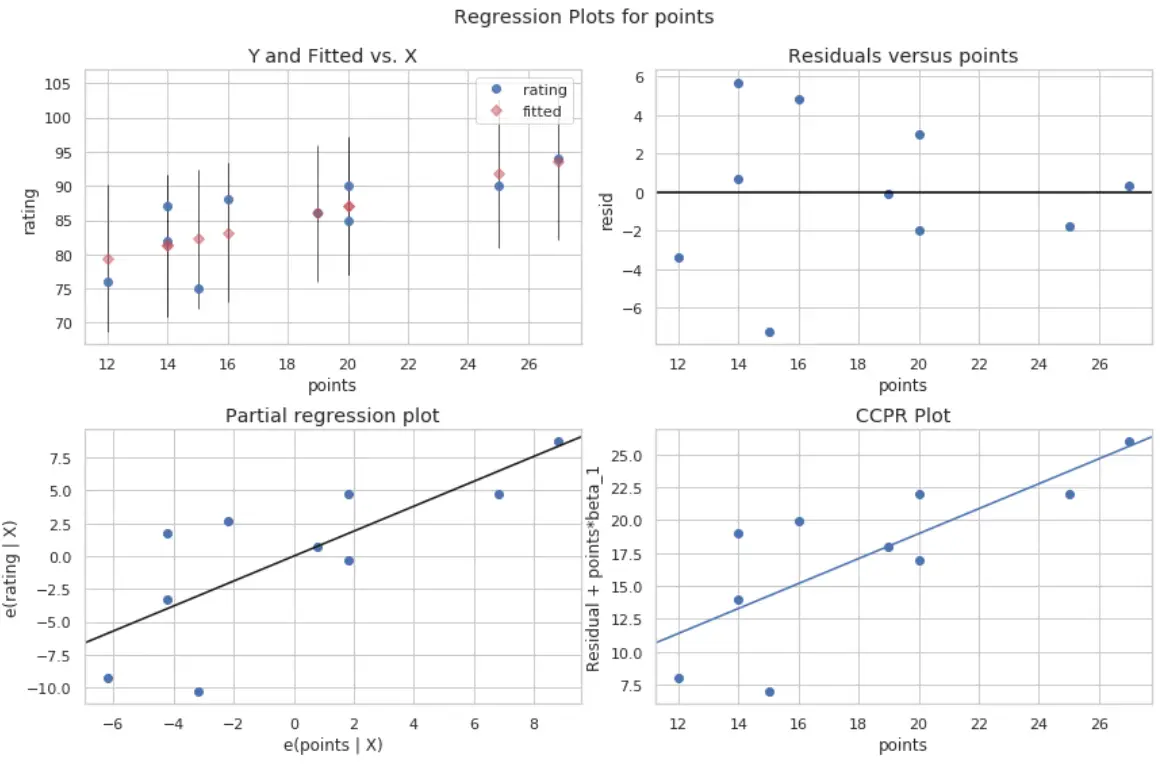
Quatre parcelles sont produites. Celui dans le coin supérieur droit est le tracé résiduel par rapport au tracé ajusté. L’axe des X sur ce tracé montre les valeurs réelles des points de variable prédictive et l’axe des Y montre le résidu pour cette valeur.
Étant donné que les résidus semblent être dispersés de manière aléatoire autour de zéro, cela indique que l’hétéroscédasticité n’est pas un problème avec la variable prédictive.
Tracés résiduels pour la régression linéaire multiple
Supposons que nous ajustions plutôt un modèle de régression linéaire multiple utilisant les passes décisives et les rebonds comme variable prédictive et la note comme variable de réponse :
#fit multiple linear regression model model = ols('rating ~ assists + rebounds', data=df).fit() #view model summary print(model.summary())
Une fois de plus, nous pouvons créer un tracé résiduel par rapport au prédicteur pour chacun des prédicteurs individuels à l’aide de la fonction plot_regress_exog() de la bibliothèque statsmodels.
Par exemple, voici à quoi ressemble le graphique résiduel/prédicteur pour les assistances de variables prédictives :
#create residual vs. predictor plot for 'assists' fig = plt.figure(figsize=(12,8)) fig = sm.graphics.plot_regress_exog(model, 'assists', fig=fig)
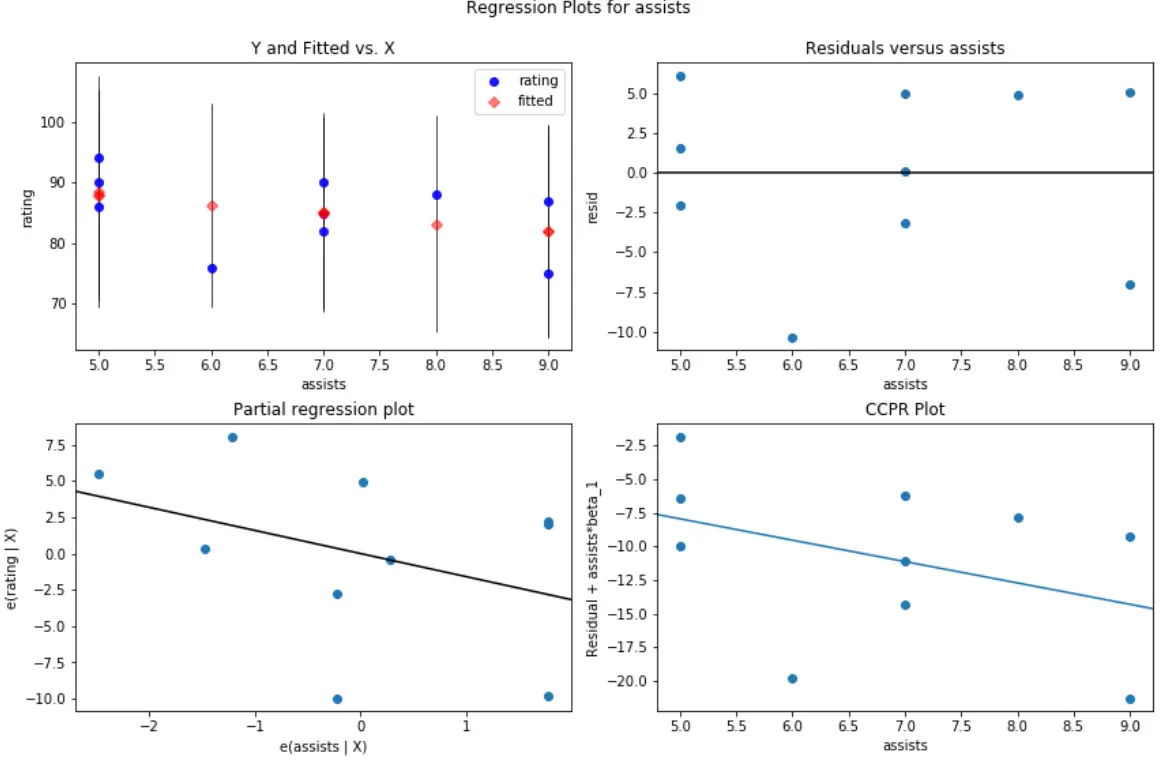
Et voici à quoi ressemble le graphique résiduel/prédicteur pour les rebonds des variables prédictives :
#create residual vs. predictor plot for 'assists' fig = plt.figure(figsize=(12,8)) fig = sm.graphics.plot_regress_exog(model, 'rebounds', fig=fig)
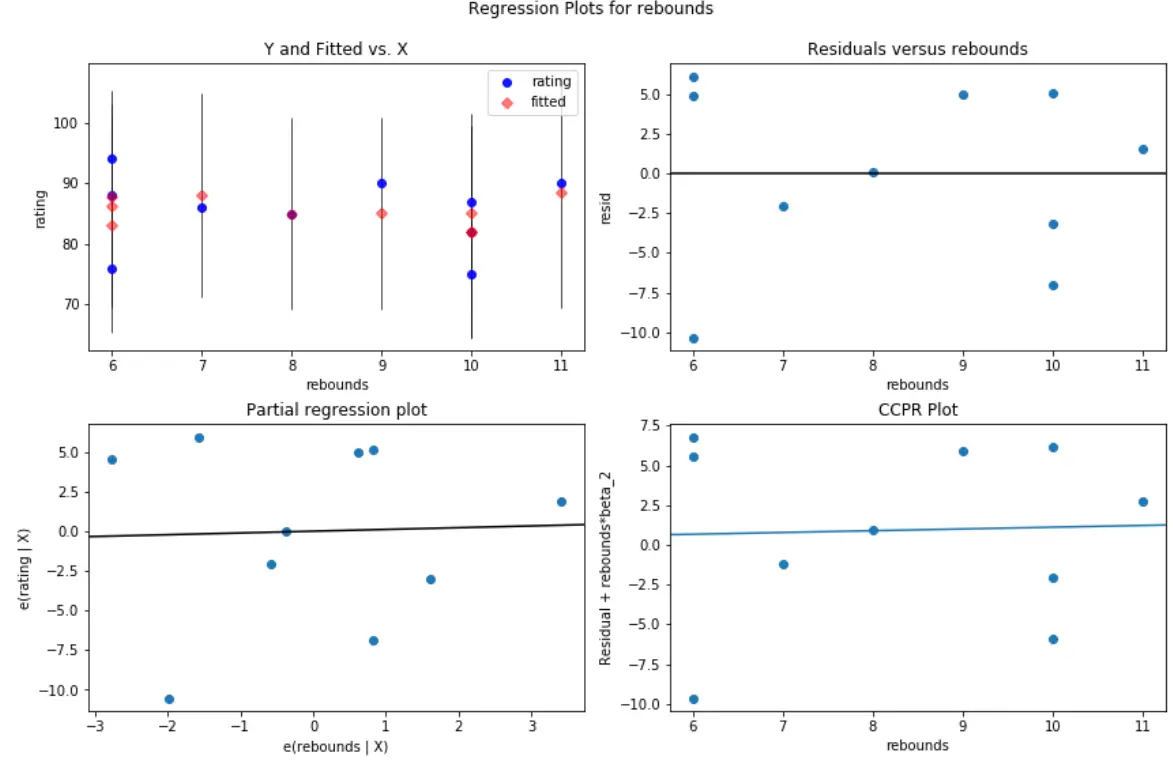
Dans les deux graphiques, les résidus semblent être dispersés de manière aléatoire autour de zéro, ce qui indique que l’hétéroscédasticité ne constitue pas un problème avec l’une ou l’autre des variables prédictives du modèle.
