Comment créer un tracé QQ en Python
Un tracé QQ , abréviation de « quantile-quantile », est souvent utilisé pour évaluer si un ensemble de données provient potentiellement ou non d’une distribution théorique.
Dans la plupart des cas, ce type de tracé est utilisé pour déterminer si un ensemble de données suit ou non une distribution normale .
Ce didacticiel explique comment créer un tracé QQ pour un ensemble de données en Python.
Exemple : tracé QQ en Python
Supposons que nous ayons l’ensemble de données suivant de 100 valeurs :
import numpy as np #create dataset with 100 values that follow a normal distribution np.random.seed(0) data = np.random.normal(0,1, 1000) #view first 10 values data[:10] array([ 1.76405235, 0.40015721, 0.97873798, 2.2408932 , 1.86755799, -0.97727788, 0.95008842, -0.15135721, -0.10321885, 0.4105985 ])
Pour créer un tracé QQ pour cet ensemble de données, nous pouvons utiliser la fonction qqplot() de la bibliothèque statsmodels :
import statsmodels.api as sm import matplotlib.pyplot as plt #create Q-Q plot with 45-degree line added to plot fig = sm.qqplot(data, line='45') plt.show()
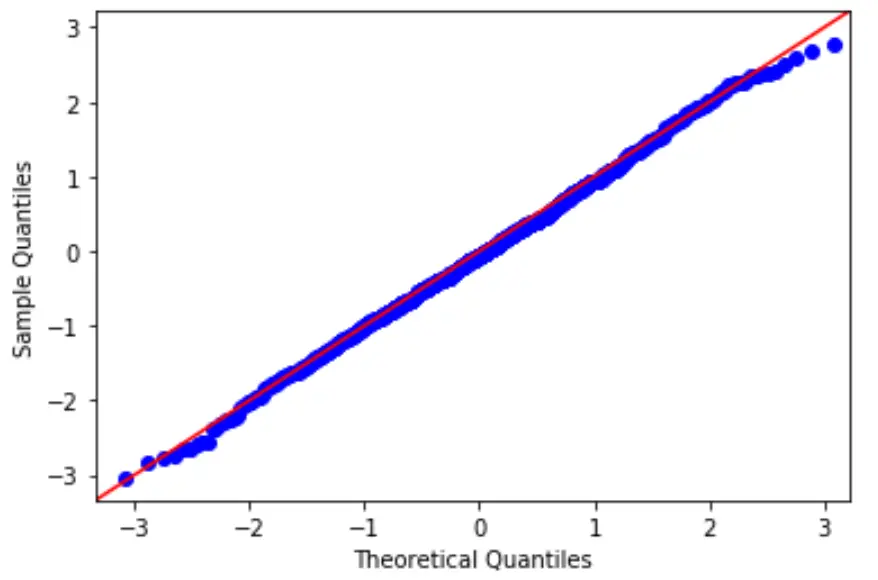
Dans un tracé QQ, l’axe des x affiche les quantiles théoriques . Cela signifie qu’il n’affiche pas vos données réelles, mais représente plutôt l’endroit où se trouveraient vos données si elles étaient normalement distribuées.
L’axe Y affiche vos données réelles . Cela signifie que si les valeurs des données suivent une ligne à peu près droite à un angle de 45 degrés, alors les données sont normalement distribuées.
Nous pouvons voir dans notre graphique QQ ci-dessus que les valeurs des données ont tendance à suivre de près les 45 degrés, ce qui signifie que les données sont probablement distribuées normalement. Cela ne devrait pas être surprenant puisque nous avons généré les 100 valeurs de données en utilisant la fonction numpy.random.normal() .
Considérons plutôt si nous générions un ensemble de données de 100 valeurs uniformément distribuées et créions un tracé QQ pour cet ensemble de données :
#create dataset of 100 uniformally distributed values data = np.random.uniform(0,1, 1000) #generate Q-Q plot for the dataset fig = sm.qqplot(data, line='45') plt.show()
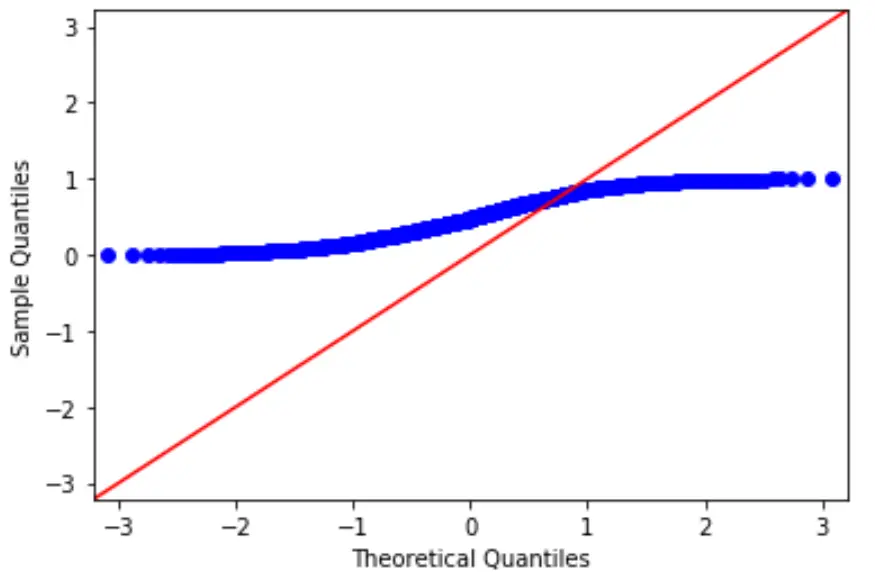
Les valeurs des données ne suivent clairement pas la ligne rouge à 45 degrés, ce qui indique qu’elles ne suivent pas une distribution normale.
Remarques sur les tracés QQ
Gardez à l’esprit les remarques suivantes concernant les tracés QQ :
- Bien qu’un tracé QQ ne soit pas un test statistique formel, il offre un moyen simple de vérifier visuellement si un ensemble de données est normalement distribué ou non.
- Veillez à ne pas confondre les tracés QQ avec les tracés PP , qui sont moins couramment utilisés et moins utiles pour analyser les valeurs de données qui se situent aux extrémités de la distribution.
Vous pouvez trouver plus de didacticiels Python ici .
