Comment utiliser la distribution binomiale en Python

La distribution binomiale est l’une des distributions les plus couramment utilisées en statistique. Il décrit la probabilité d’obtenir k succès dans n expériences binomiales.

Si une variable aléatoire X suit une distribution binomiale, alors la probabilité que X = k succès peut être trouvée par la formule suivante :

P(X=k) = _n C _k * p ^k * (1-p) ^nk

où:

• n : nombre d’essais
• k : nombre de réussites
• p : probabilité de succès sur un essai donné
• _n C _k : le nombre de façons d’obtenir k succès dans n essais

Ce tutoriel explique comment utiliser la distribution binomiale en Python.

Comment générer une distribution binomiale

Vous pouvez générer un tableau de valeurs qui suivent une distribution binomiale en utilisant la fonction random.binomial de la bibliothèque numpy :

from numpy import random

#generate an array of 10 values that follow a binomial distribution
random.binomial(n=10, p=.25, size=10)

array([5, 2, 1, 3, 3, 3, 2, 2, 1, 4])

Chaque nombre dans le tableau résultant représente le nombre de « succès » rencontrés au cours de 10 essais où la probabilité de succès dans un essai donné était de 0,25 .

Comment calculer les probabilités à l’aide d’une distribution binomiale

Vous pouvez également répondre à des questions sur les probabilités binomiales en utilisant la fonction binom de la bibliothèque scipy.

Question 1 : Nathan réalise 60% de ses tentatives de lancer franc. S’il réussit 12 lancers francs, quelle est la probabilité qu’il en réalise exactement 10 ?

from scipy.stats import binom

#calculate binomial probability
binom.pmf(k=10, n=12, p=0.6)

0.0639

La probabilité que Nathan réalise exactement 10 lancers francs est de 0,0639 .

Question 2 : Marty lance une pièce de monnaie équitable 5 fois. Quelle est la probabilité que la pièce tombe sur face 2 fois ou moins ?

from scipy.stats import binom

#calculate binomial probability
binom.cdf(k=2, n=5, p=0.5)

0.5

La probabilité que la pièce tombe sur face 2 fois ou moins est de 0,5 .

Question 3 : On sait que 70 % des individus soutiennent une certaine loi. Si 10 individus sont sélectionnés au hasard, quelle est la probabilité qu’entre 4 et 6 d’entre eux soutiennent la loi ?

from scipy.stats import binom

#calculate binomial probability
binom.cdf(k=6, n=10, p=0.7) - binom.cdf(k=3, n=10, p=0.7)

0.3398

La probabilité qu’entre 4 et 6 des individus sélectionnés au hasard soutiennent la loi est de 0,3398 .

Comment visualiser une distribution binomiale

Vous pouvez visualiser une distribution binomiale en Python en utilisant les bibliothèques seaborn et matplotlib :

from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns

x = random.binomial(n=10, p=0.5, size=1000)

sns.distplot(x, hist=True, kde=False)

plt.show()

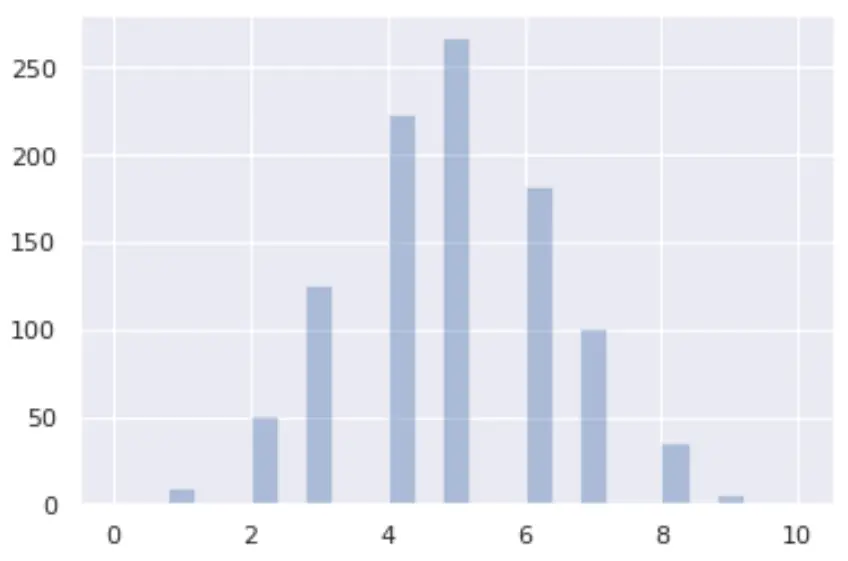
L’axe des X décrit le nombre de réussites au cours de 10 essais et l’axe des Y affiche le nombre de fois où chaque nombre de réussites s’est produit au cours de 1 000 expériences.