Comment créer une matrice de covariance en Python

La covariance est une mesure de la façon dont les changements dans une variable sont associés aux changements dans une deuxième variable. Plus précisément, il s’agit d’une mesure du degré auquel deux variables sont linéairement associées.

Une matrice de covariance est une matrice carrée qui montre la covariance entre de nombreuses variables différentes. Cela peut être un moyen utile de comprendre comment les différentes variables sont liées dans un ensemble de données.

L’exemple suivant montre comment créer une matrice de covariance en Python.

Comment créer une matrice de covariance en Python

Utilisez les étapes suivantes pour créer une matrice de covariance en Python.

Étape 1 : Créez l’ensemble de données.

Tout d’abord, nous allons créer un ensemble de données contenant les résultats des tests de 10 élèves différents dans trois matières : les mathématiques, les sciences et l’histoire.

import numpy as np

math = [84, 82, 81, 89, 73, 94, 92, 70, 88, 95]
science = [85, 82, 72, 77, 75, 89, 95, 84, 77, 94]
history = [97, 94, 93, 95, 88, 82, 78, 84, 69, 78]

data = np.array([math, science, history])

Étape 2 : Créez la matrice de covariance.

Ensuite, nous allons créer la matrice de covariance pour cet ensemble de données à l’aide de la fonction numpy cov() , en spécifiant que biais = True afin que nous puissions calculer la matrice de covariance de la population.

np.cov(data, bias=True)

array([[ 64.96,  33.2 , -24.44],
       [ 33.2 ,  56.4 , -24.1 ],
       [-24.44, -24.1 ,  75.56]])

Étape 3 : Interprétez la matrice de covariance.

Les valeurs le long des diagonales de la matrice sont simplement les variances de chaque sujet. Par exemple:

• La variance des résultats en mathématiques est de 64,96
• La variance des scores en sciences est de 56,4
• La variance des scores historiques est de 75,56

Les autres valeurs de la matrice représentent les covariances entre les différents sujets. Par exemple:

• La covariance entre les scores en mathématiques et en sciences est de 33,2.
• La covariance entre les scores en mathématiques et en histoire est de -24,44.
• La covariance entre les scores en sciences et en histoire est de -24,1.

Un nombre positif pour la covariance indique que deux variables ont tendance à augmenter ou à diminuer en tandem. Par exemple, les mathématiques et les sciences ont une covariance positive (33,2), ce qui indique que les élèves qui obtiennent des résultats élevés en mathématiques ont également tendance à obtenir des résultats élevés en sciences. À l’inverse, les élèves qui obtiennent de faibles résultats en mathématiques ont également tendance à obtenir de faibles résultats en sciences.

Un nombre négatif pour la covariance indique que lorsqu’une variable augmente, une deuxième variable a tendance à diminuer. Par exemple, les mathématiques et l’histoire ont une covariance négative (-24,44), ce qui indique que les élèves qui obtiennent des résultats élevés en mathématiques ont tendance à avoir des résultats faibles en histoire. À l’inverse, les élèves qui obtiennent de faibles résultats en mathématiques ont tendance à obtenir des résultats élevés en histoire.

Étape 4 : Visualisez la matrice de covariance (facultatif).

Vous pouvez visualiser la matrice de covariance en utilisant la fonction heatmap() du package seaborn :

import seaborn as sns
import matplotlib.pyplot as plt

cov = np.cov(data, bias=True)
labs = ['math', 'science', 'history']

sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs)
plt.show()

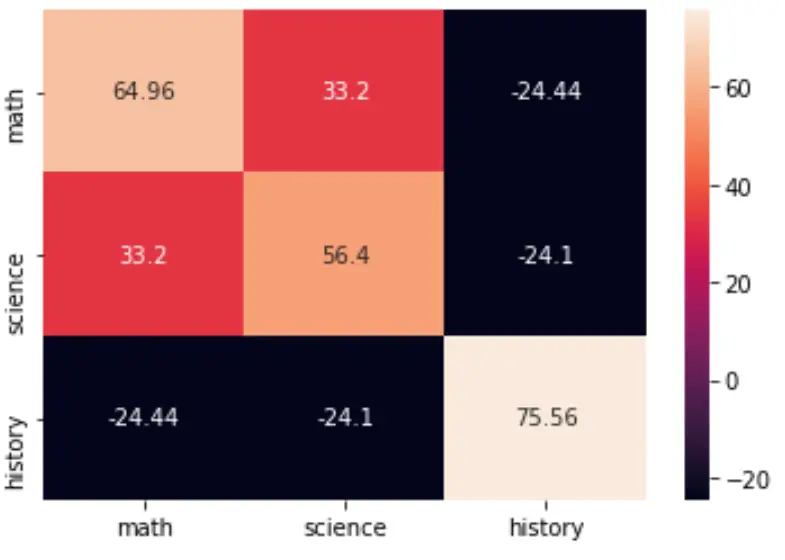
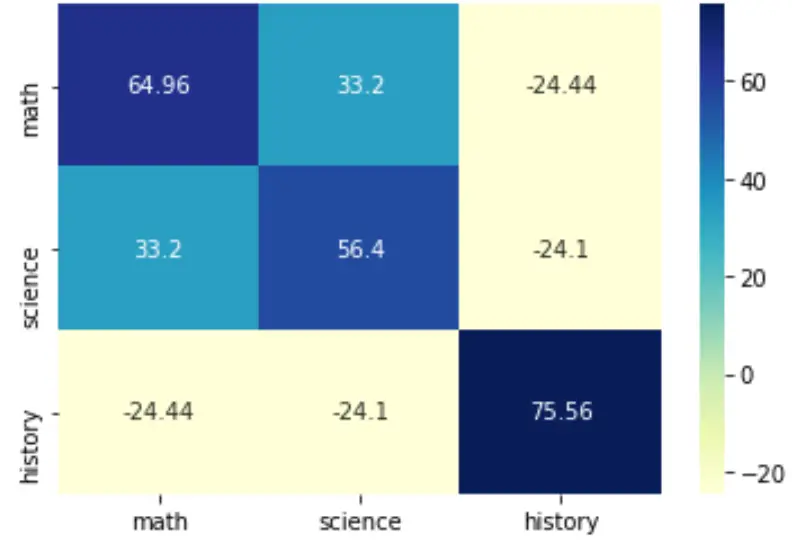
Vous pouvez également modifier la palette de couleurs en spécifiant l’argument cmap :

sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs, cmap='YlGnBu')
plt.show()

Pour plus de détails sur la façon de styliser cette carte thermique, reportez-vous à la documentation seaborn .