Qu’est-ce qu’une distribution bimodale ?

Une distribution bimodale est une distribution de probabilité à deux modes.

Nous utilisons souvent le terme « mode » dans les statistiques descriptives pour désigner la valeur la plus courante dans un ensemble de données, mais dans ce cas, le terme « mode » fait référence à un maximum local dans un graphique.

Lorsque vous visualisez une distribution bimodale, vous remarquerez deux « pics » distincts qui représentent ces deux modes.

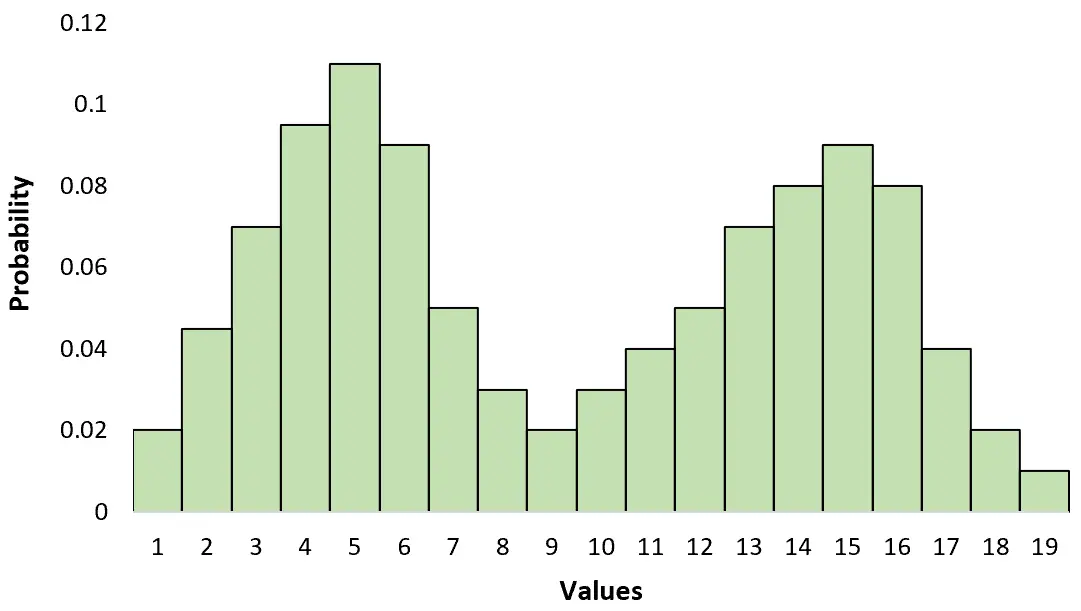
Ceci est différent d’une distribution unimodale qui n’a qu’un seul pic :

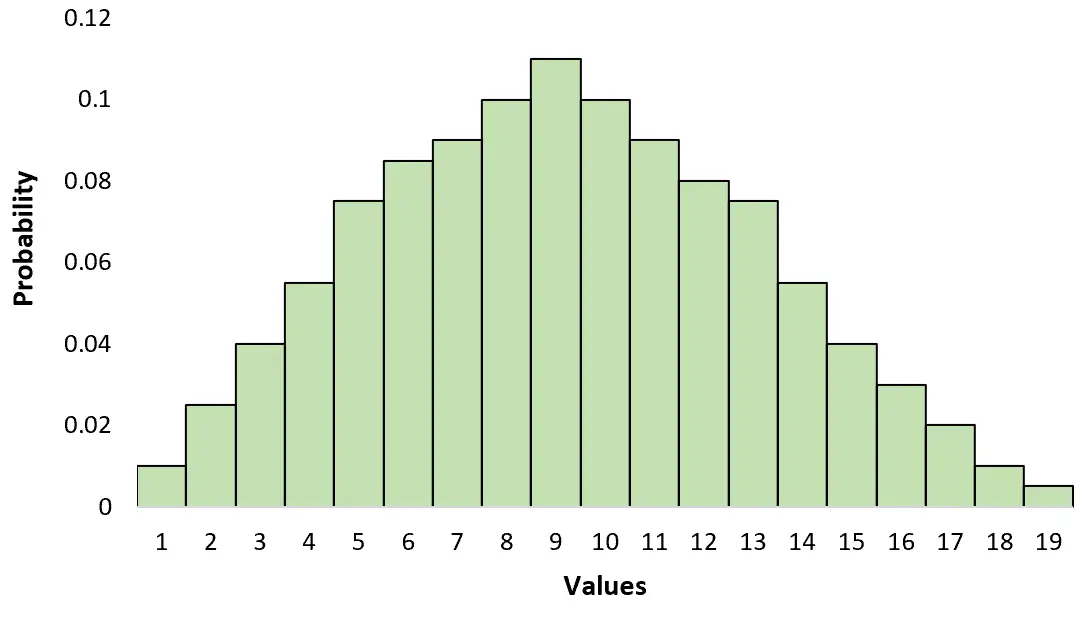
Vous pouvez vous souvenir de la différence entre les deux en vous rappelant :

• « bi » = deux
• « uni » = un

Bien que la plupart des cours de statistiques utilisent des distributions unimodales comme la distribution normale pour expliquer différents sujets, les distributions bimodales apparaissent assez souvent dans la pratique, il est donc utile de savoir comment les reconnaître et les interpréter.

Remarque : Une distribution bimodale est un type spécifique de distribution multimodale .

Exemples de distributions bimodales

Voici quelques exemples de distributions bimodales :

Exemple n°1 : Heures de pointe du restaurant

Si vous créiez un graphique pour visualiser la répartition horaire des clients dans un certain restaurant, vous constateriez probablement qu’il suit une distribution bimodale avec un pic pendant les heures de déjeuner et un autre pic pendant les heures de dîner :

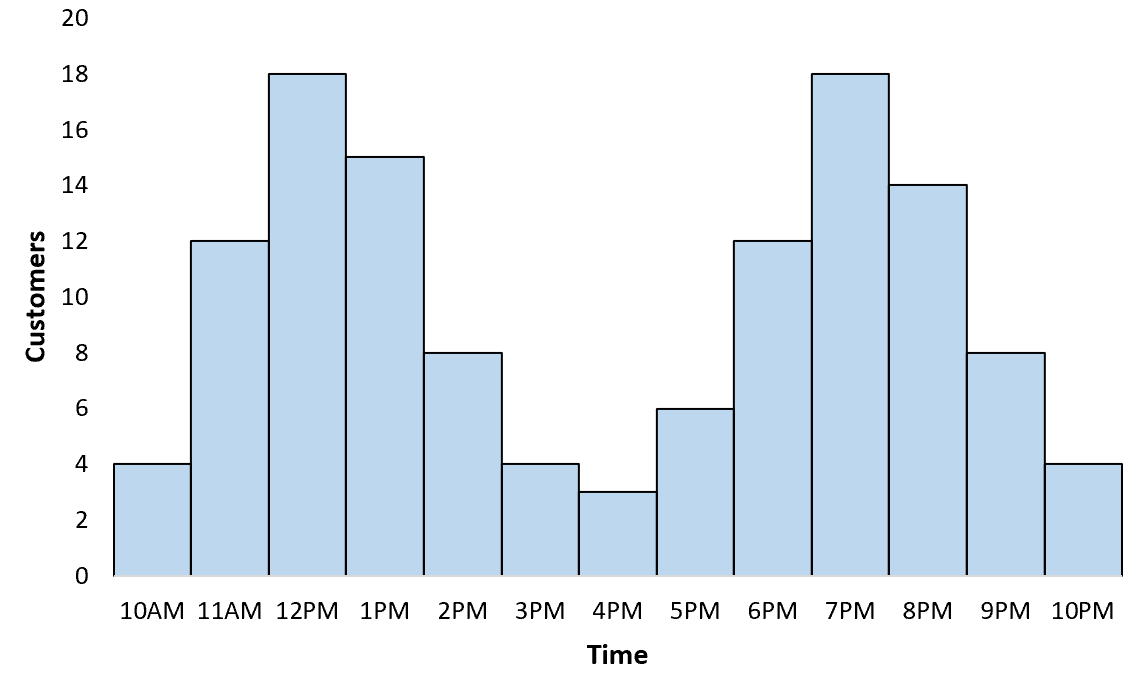
Exemple n°2 : Hauteur moyenne de deux espèces végétales

Supposons que vous fassiez le tour d’un champ et que vous mesuriez la hauteur de différentes plantes. Sans vous en rendre compte, vous mesurez la taille de deux espèces différentes : une assez grande et une autre assez petite. Si vous créiez un graphique pour visualiser la répartition des hauteurs, il suivrait une distribution bimodale :

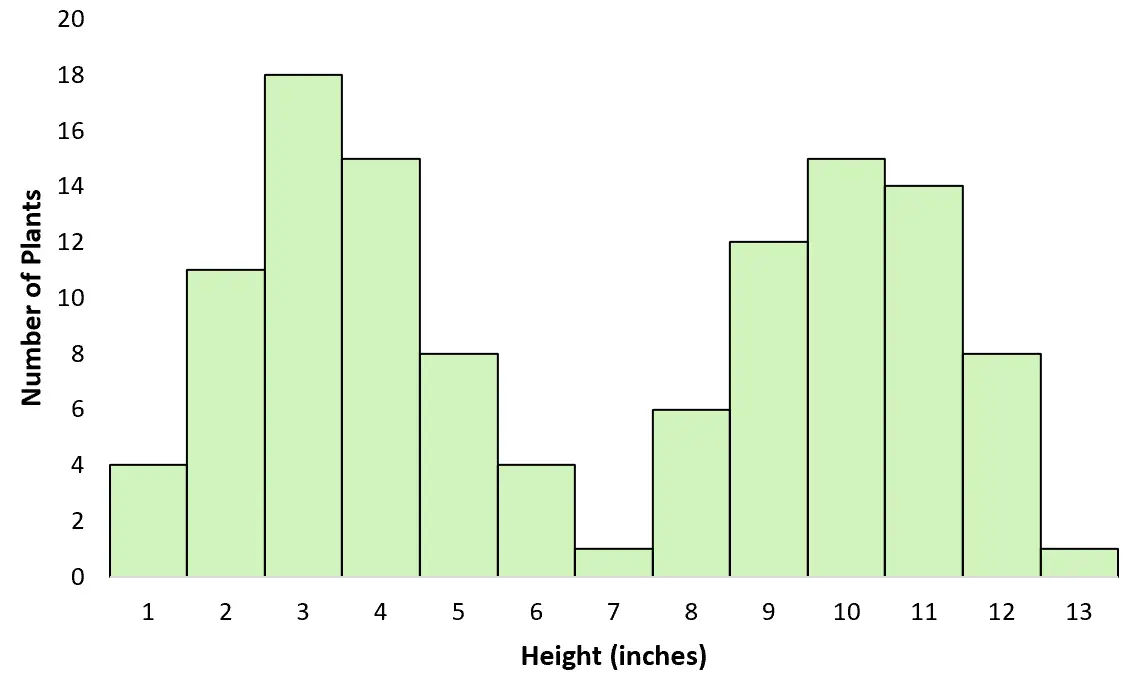
Exemple n°3 : résultats des examens

Supposons qu’un enseignant donne un examen à sa classe d’élèves. Certains étudiants ont étudié pour l’examen, d’autres non. Lorsque l’enseignant crée un graphique des résultats des examens, il suit une distribution bimodale avec un pic autour des scores faibles pour les étudiants qui n’ont pas étudié et un autre pic autour des scores élevés pour les étudiants qui ont étudié :

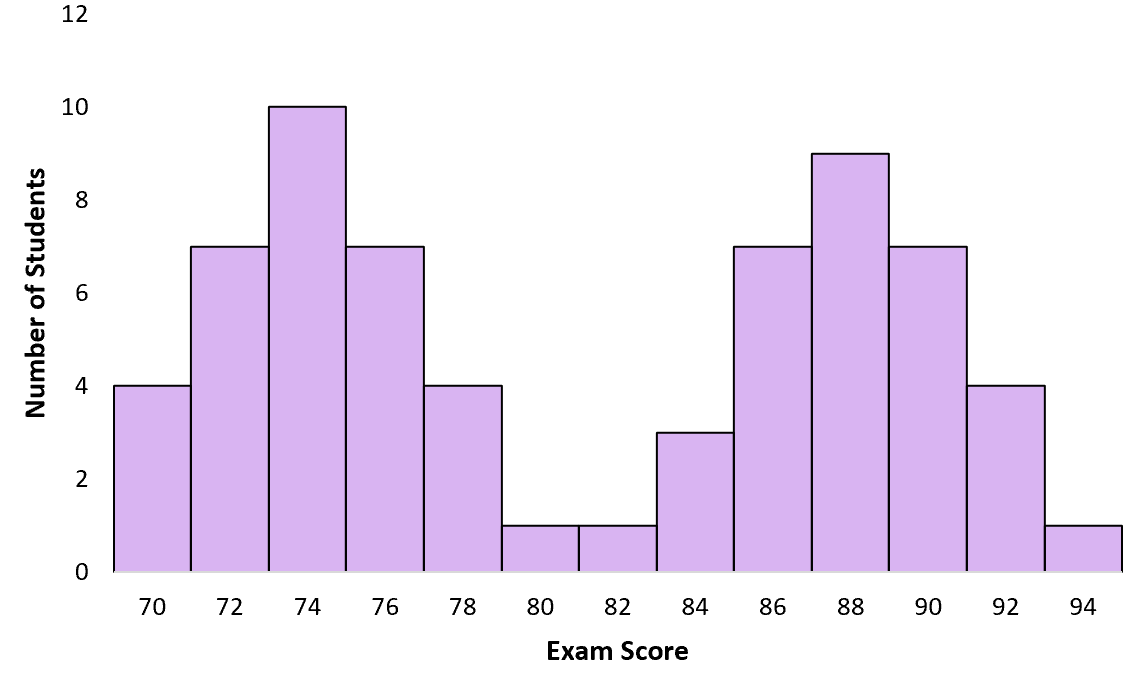
Quelles sont les causes des distributions bimodales ?

Il y a généralement deux choses qui provoquent des distributions bimodales :

1. Quelques phénomènes sous-jacents.

Les distributions bimodales se produisent souvent en raison de certains phénomènes sous-jacents.

Par exemple, le nombre de clients qui visitent un restaurant chaque heure suit une distribution bimodale puisque les gens ont tendance à manger au restaurant à deux moments distincts : le déjeuner et le dîner. Ce comportement humain sous-jacent est à l’origine de la distribution bimodale.

2. Deux groupes différents regroupés.

Les distributions bimodales peuvent également se produire lorsque vous analysez simplement deux groupes de choses différents sans vous en rendre compte.

Par exemple, si vous mesurez la hauteur des plantes dans un certain champ sans vous rendre compte que deux espèces différentes poussent dans le même champ, vous verrez une distribution bimodale lorsque vous créerez un graphique.

Comment analyser les distributions bimodales

Nous décrivons souvent les distributions en utilisant la moyenne ou la médiane car cela nous donne une idée de l’endroit où se trouve le « centre » de la distribution.

Malheureusement, la moyenne et la médiane ne sont pas utiles à connaître pour une distribution bimodale. Par exemple, la note moyenne à l’examen des étudiants de l’exemple ci-dessus est de 81 :

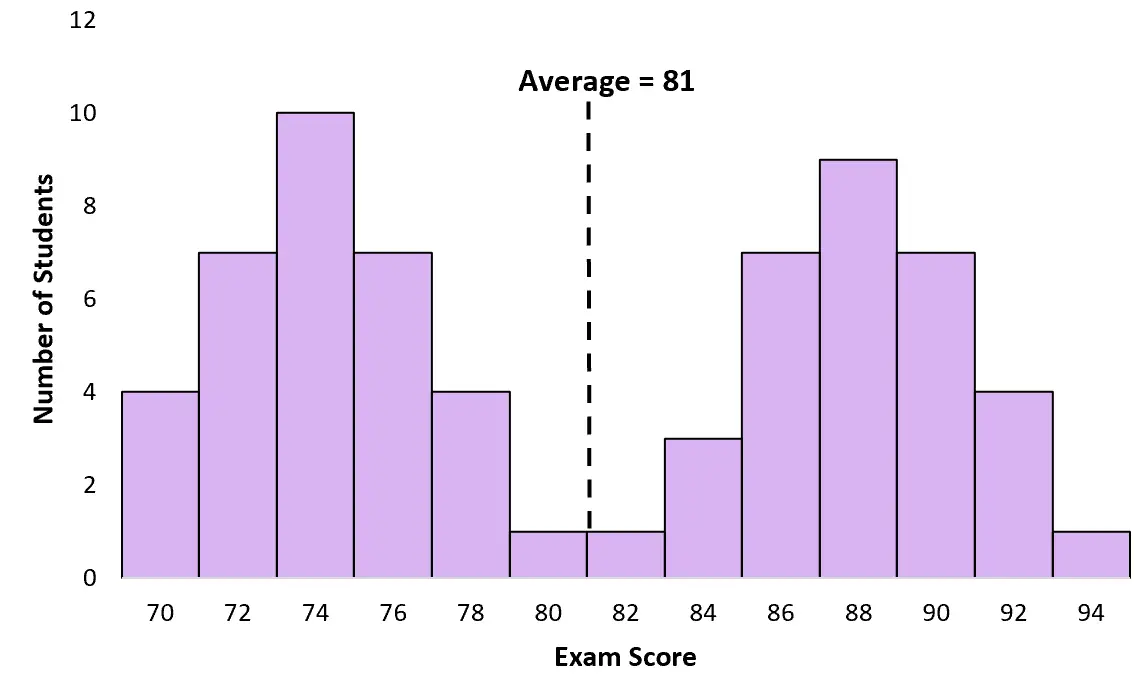
Cependant, très peu d’élèves ont obtenu un score proche de 81. Dans ce cas, la moyenne est trompeuse. La plupart des étudiants ont en fait obtenu un score d’environ 74 ou 88.

Une meilleure façon d’analyser et d’interpréter les distributions bimodales consiste simplement à diviser les données en deux groupes distincts, puis à analyser le centre et la répartition pour chaque groupe.

Par exemple, nous pouvons diviser les résultats des examens en « scores faibles » et « scores élevés », puis trouver la moyenne et l’écart type pour chaque groupe.

Si vous partagez les résultats d’une analyse et que vos données suivent une distribution bimodale, il est utile de créer un histogramme comme ceux présentés ci-dessus afin que votre public puisse voir clairement que la distribution a deux « pics » distincts et qu’elle ne fait que Il est logique d’analyser chaque pic séparément plutôt que comme un seul grand ensemble de données.