Comment calculer les scores Z dans SPSS

Un score z nous indique à combien d’écarts types une valeur donnée se trouve par rapport à la moyenne.

Le score z d’une valeur donnée est calculé comme suit :

Score z = (x – μ) / σ

où:

• x : valeur individuelle
• μ : moyenne de la population
• σ : écart type de la population

Ce didacticiel explique comment calculer les scores z dans SPSS.

Connexes : Comment interpréter les scores Z

Comment calculer les scores Z dans SPSS

Supposons que nous disposions de l’ensemble de données suivant qui montre le revenu annuel (en milliers) de 15 personnes :

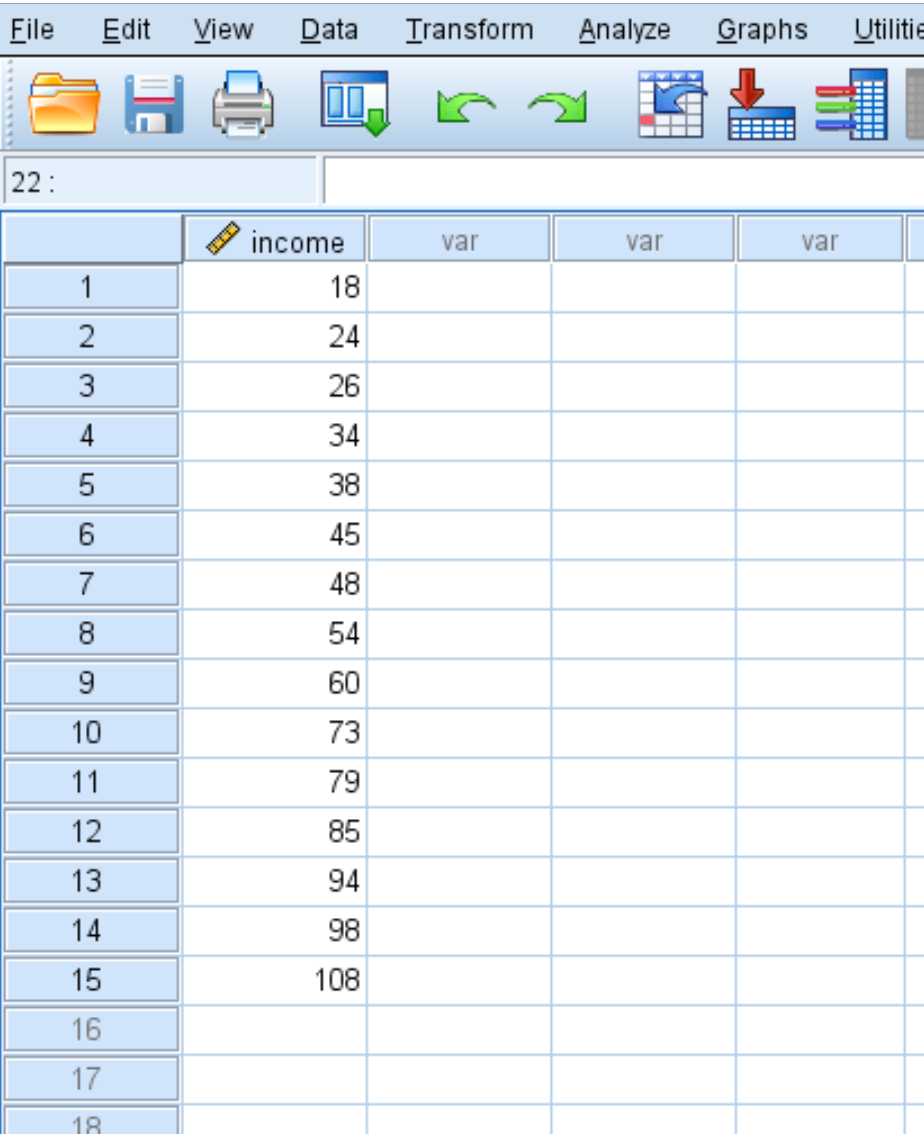
Pour calculer les scores z pour chaque valeur de l’ensemble de données, cliquez sur l’onglet Analyser , puis sur Statistiques descriptives , puis sur Descriptives :

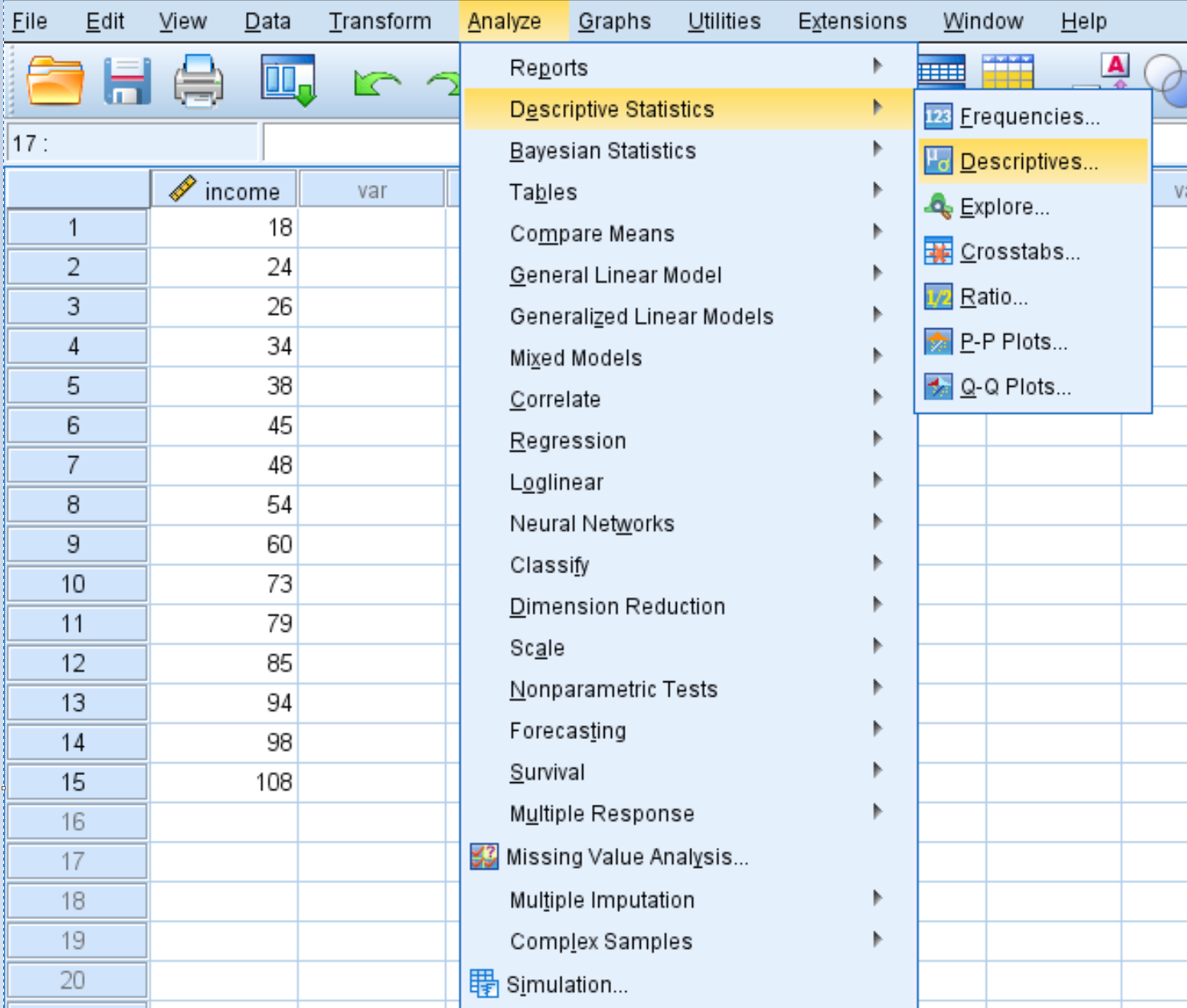
Dans la nouvelle fenêtre qui apparaît, faites glisser la variable revenu dans la case intitulée Variable(s).

Assurez-vous que la case est cochée à côté de Enregistrer les valeurs standardisées en tant que variables , puis cliquez sur OK .

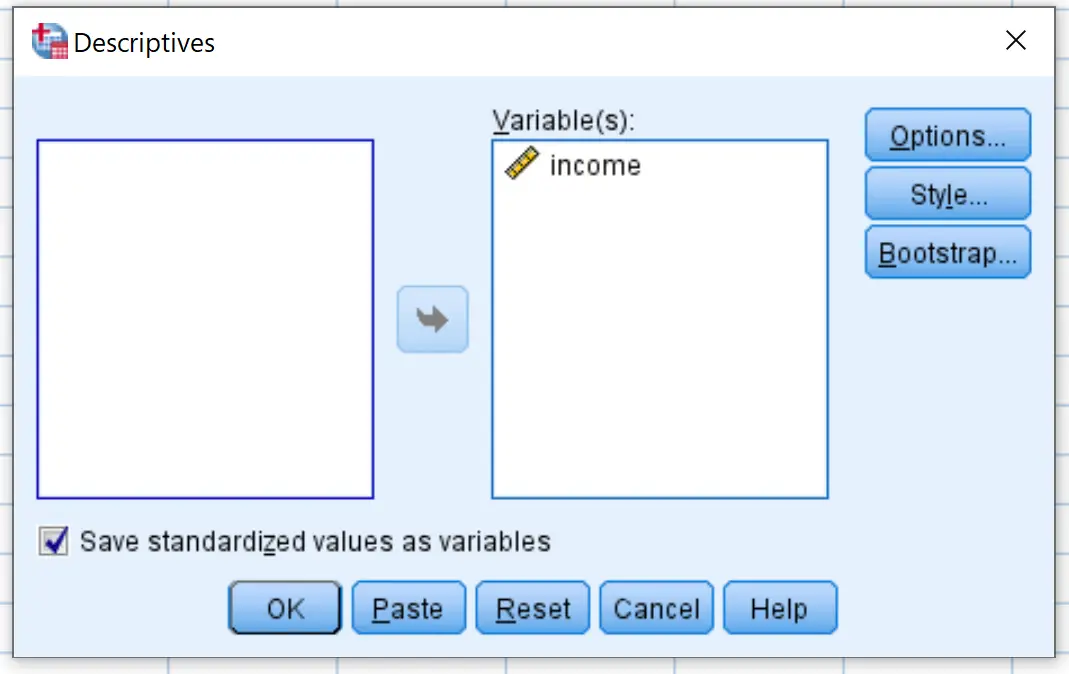
Une fois que vous avez cliqué sur OK , SPSS produira un tableau de statistiques descriptives pour votre ensemble de données :

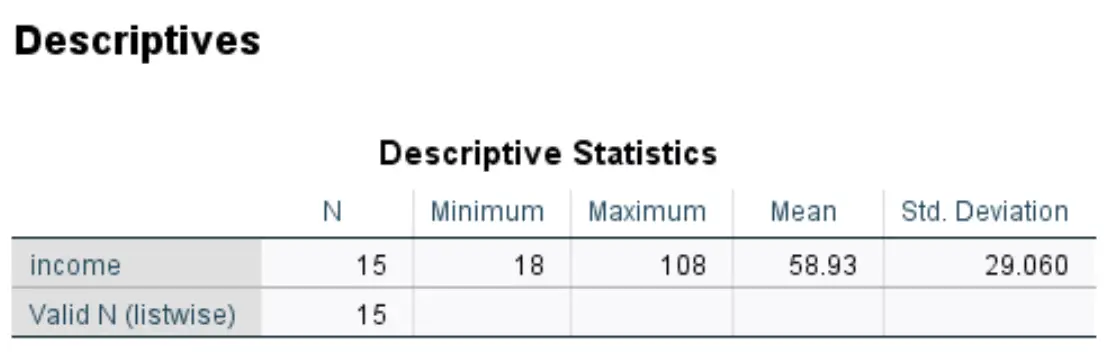
SPSS produira également une nouvelle colonne de valeurs qui affiche le z-score pour chacune des valeurs d’origine de votre ensemble de données :

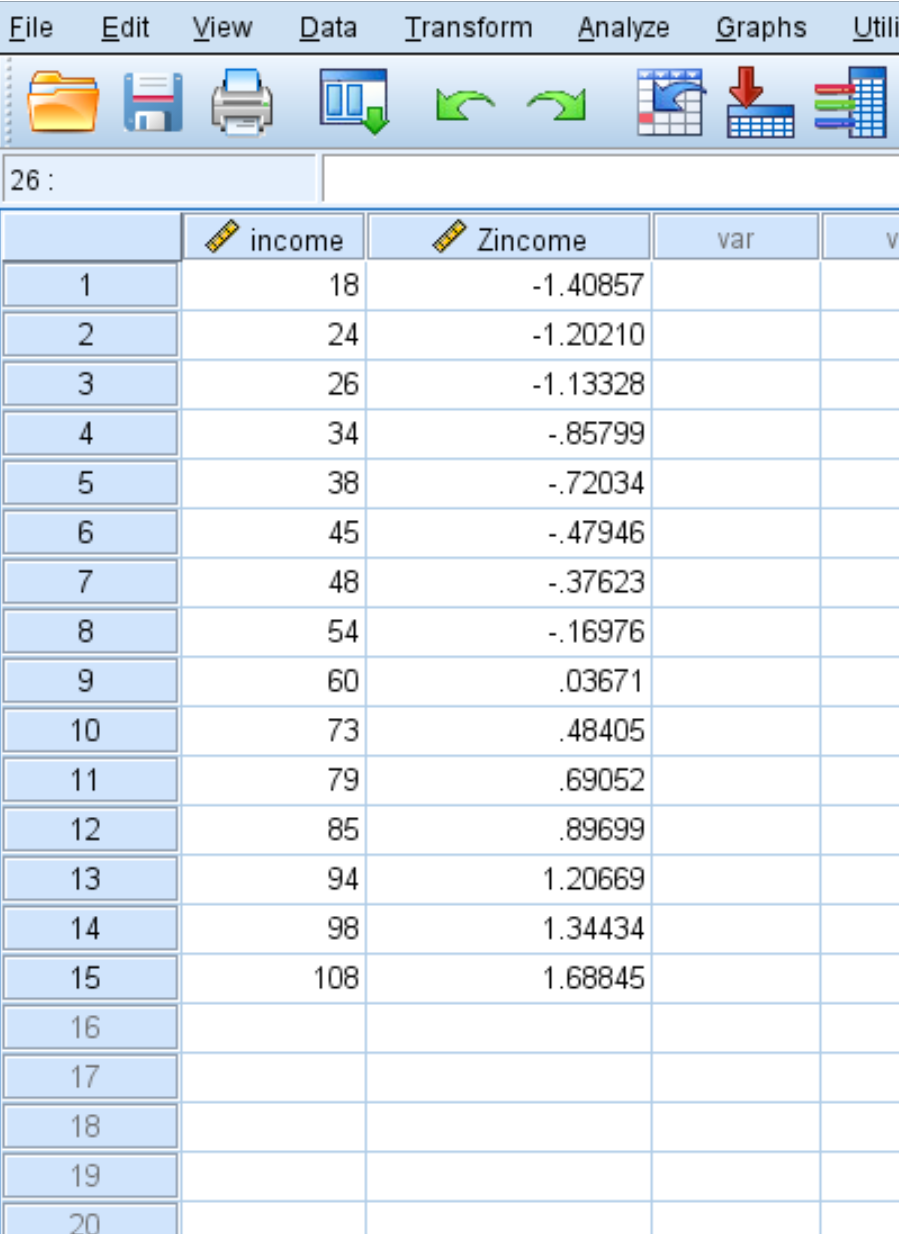
Chacun des scores z est calculé à l’aide de la formule z = (x – μ) / σ

Par exemple, le score z pour la valeur de revenu de 18 est le suivant :

z = (18 – 58,93) / 29,060 = -1,40857 .

Les scores z pour toutes les autres valeurs de données sont calculés de la même manière.

Comment interpréter les scores Z

Rappelez-vous qu’un score z nous indique simplement à combien d’écarts types une valeur se trouve par rapport à la moyenne.

Un score z peut être positif, négatif ou égal à zéro :

• Un score z positif indique qu’une valeur particulière est supérieure à la moyenne.
• Un score z négatif indique qu’une valeur particulière est inférieure à la moyenne.
• Un score z de zéro indique qu’une valeur particulière est égale à la moyenne.

Dans notre exemple, nous avons constaté que la moyenne était de 58,93 et l’écart type de 29,060.

Ainsi, la première valeur de notre ensemble de données était 18, qui avait un score z de (18 – 58,93) / 29,060 = -1,40857 .

Cela signifie que la valeur « 18 » est inférieure de 1,40857 écart-type à la moyenne.

À l’inverse, la dernière valeur de nos données était 108, ce qui correspondait à un score z de (108 – 58,93) / 29,060 = 1,68845 .

Cela signifie que la valeur « 108 » est de 1,68845 écarts-types au-dessus de la moyenne.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans SPSS :

Comment calculer des statistiques descriptives pour les variables dans SPSS
Comment calculer un résumé à cinq chiffres dans SPSS
Comment identifier les valeurs aberrantes dans SPSS