Comment effectuer une ANOVA unidirectionnelle dans SPSS

Une ANOVA unidirectionnelle est utilisée pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes indépendants ou plus.

Ce type de test est appelé ANOVA unidirectionnelle car nous analysons l’impact d’une variable prédictive sur une variable de réponse.

Si nous nous intéressions plutôt à l’impact de deux variables prédictives sur une variable de réponse, nous pourrions effectuer une ANOVA bidirectionnelle .

Ce didacticiel explique comment effectuer une ANOVA unidirectionnelle dans SPSS.

Exemple : ANOVA unidirectionnelle dans SPSS

Supposons qu’un chercheur recrute 30 étudiants pour participer à une étude. Les étudiants sont assignés au hasard à utiliser l’une des trois techniques d’étude le mois suivant pour se préparer à un examen. A la fin du mois, tous les étudiants passent le même test.

Les résultats des tests des étudiants sont indiqués ci-dessous :

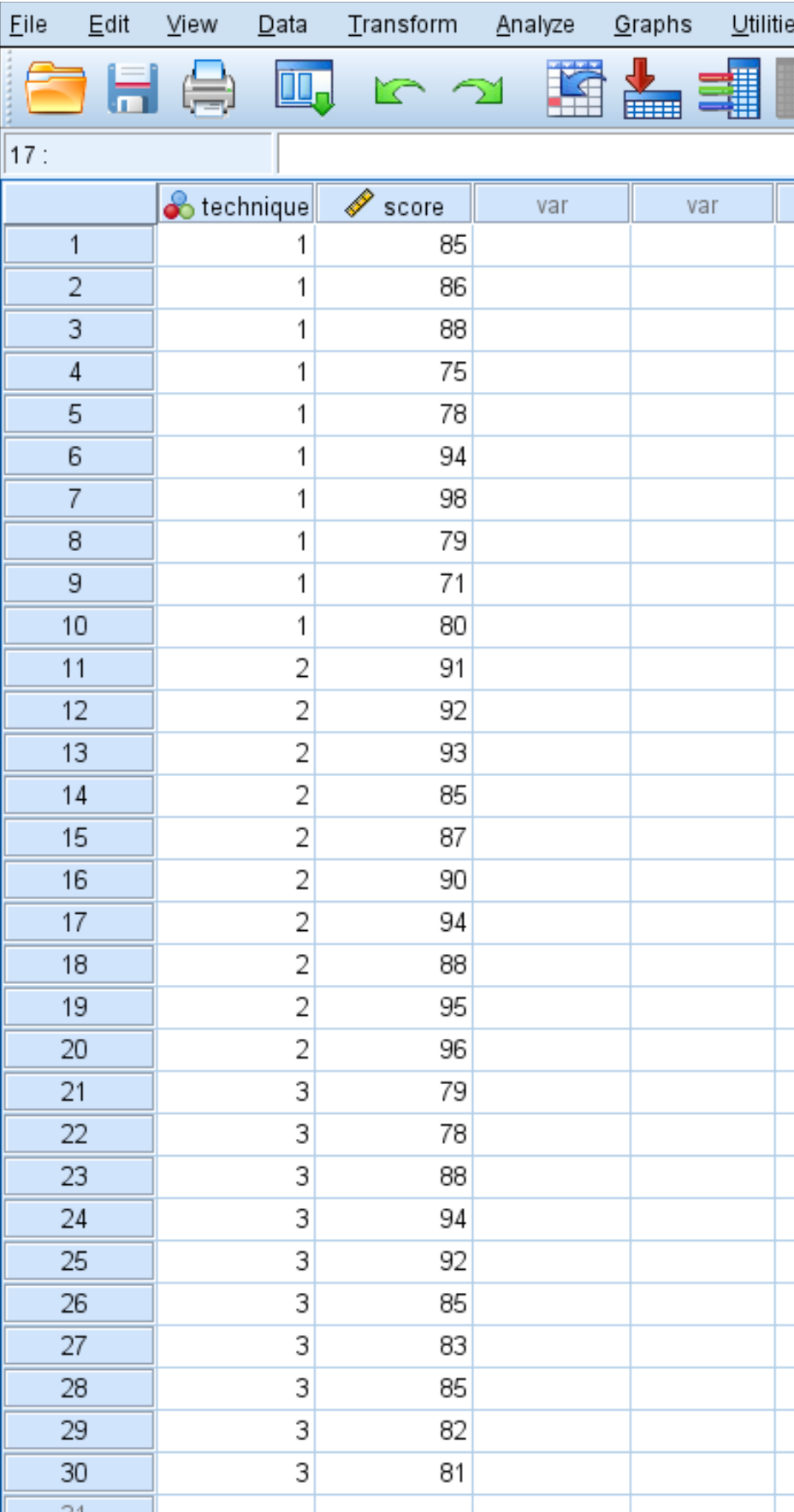
Utilisez les étapes suivantes pour effectuer une ANOVA unidirectionnelle afin de déterminer si les scores moyens sont les mêmes dans les trois groupes.

Étape 1 : Visualisez les données.

Tout d’abord, nous allons créer des boxplots pour visualiser la distribution des résultats des tests pour chacune des trois techniques d’étude. Cliquez sur l’onglet Graphiques , puis sur Générateur de graphiques .

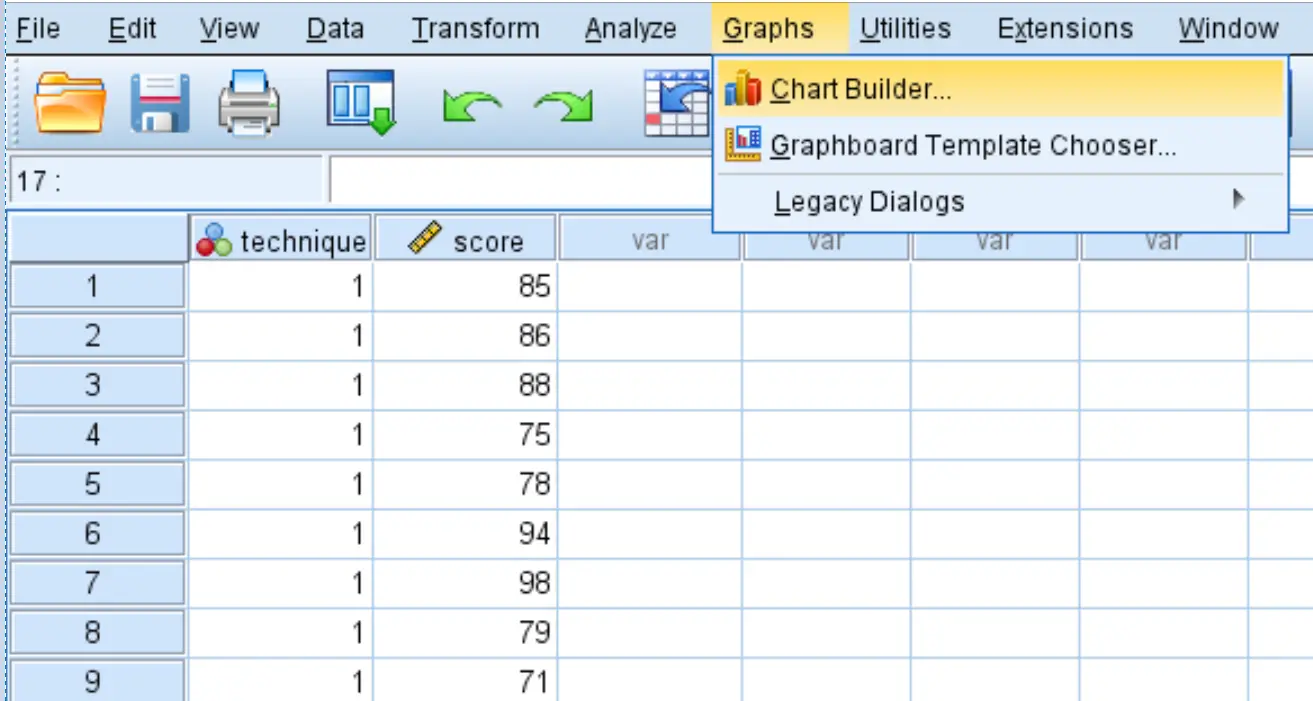
Sélectionnez Boxplot dans la fenêtre Choisir parmi : . Faites ensuite glisser le premier graphique intitulé Simple boxplot dans la fenêtre d’édition principale. Faites glisser la technique variable sur l’axe des x et le score sur l’axe des y.

Cliquez ensuite sur Propriétés des éléments , puis sur Axe Y1 . Modifiez la valeur minimale à 60. Cliquez ensuite sur OK .

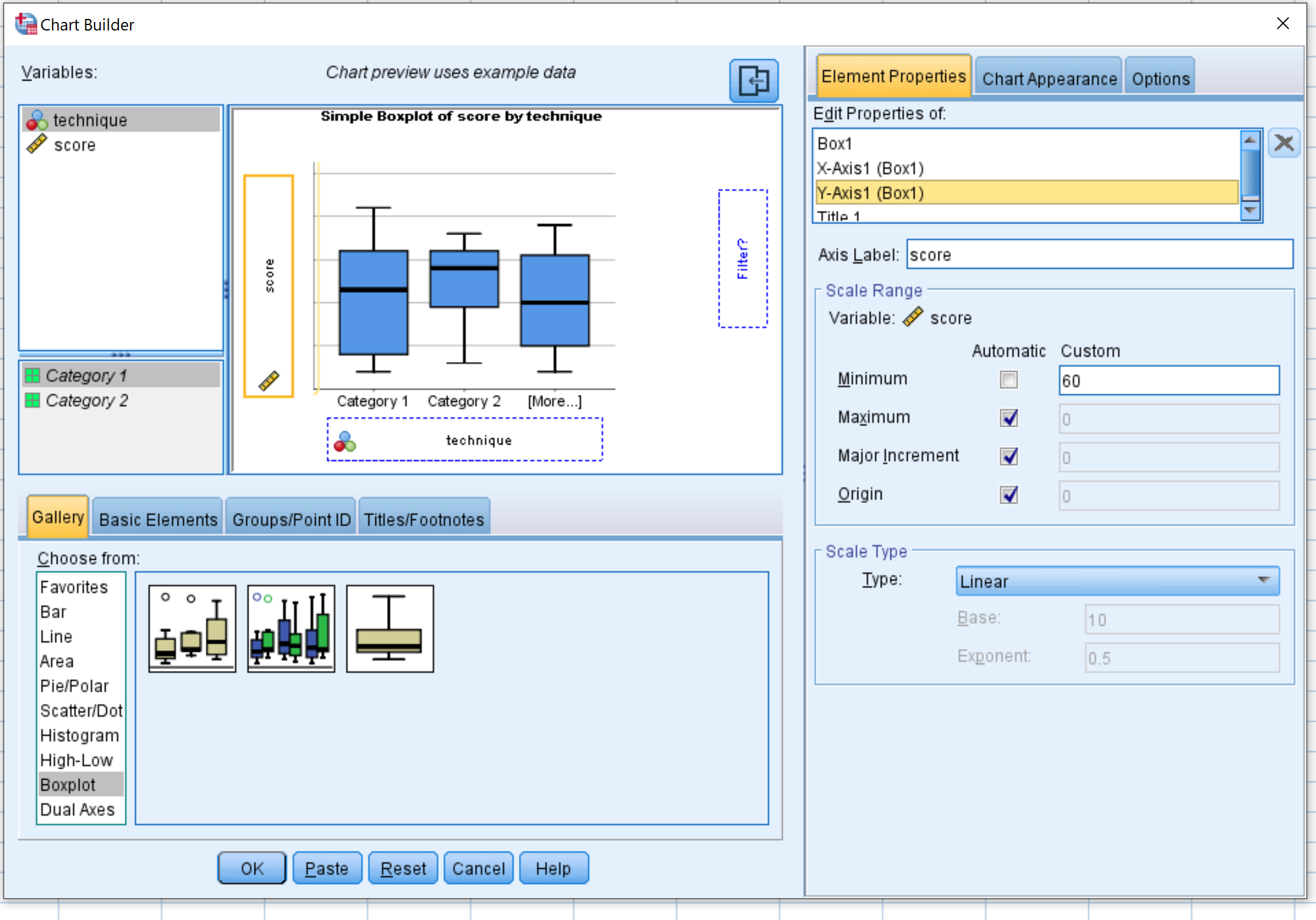
Les boîtes à moustaches suivantes apparaîtront :

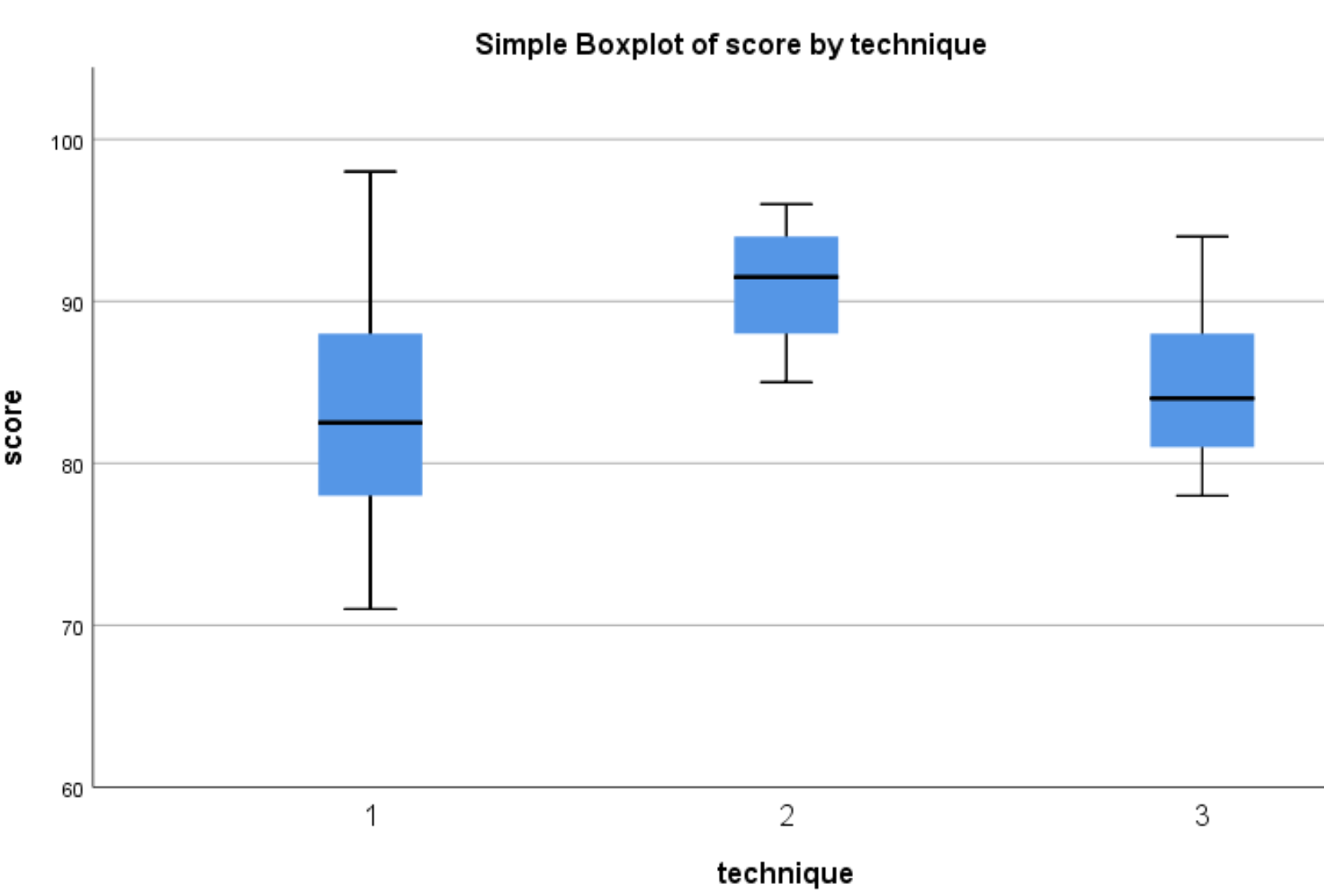
Nous pouvons voir que la distribution des résultats aux tests a tendance à être plus élevée pour les étudiants qui ont utilisé la technique 2 que pour les étudiants qui ont utilisé les techniques 1 et 3. Pour déterminer si ces différences de scores sont statistiquement significatives, nous effectuerons une ANOVA unidirectionnelle.

Étape 2 : Effectuez une ANOVA unidirectionnelle.

Cliquez sur l’onglet Analyser , puis sur Comparer les moyennes , puis sur ANOVA unidirectionnelle .

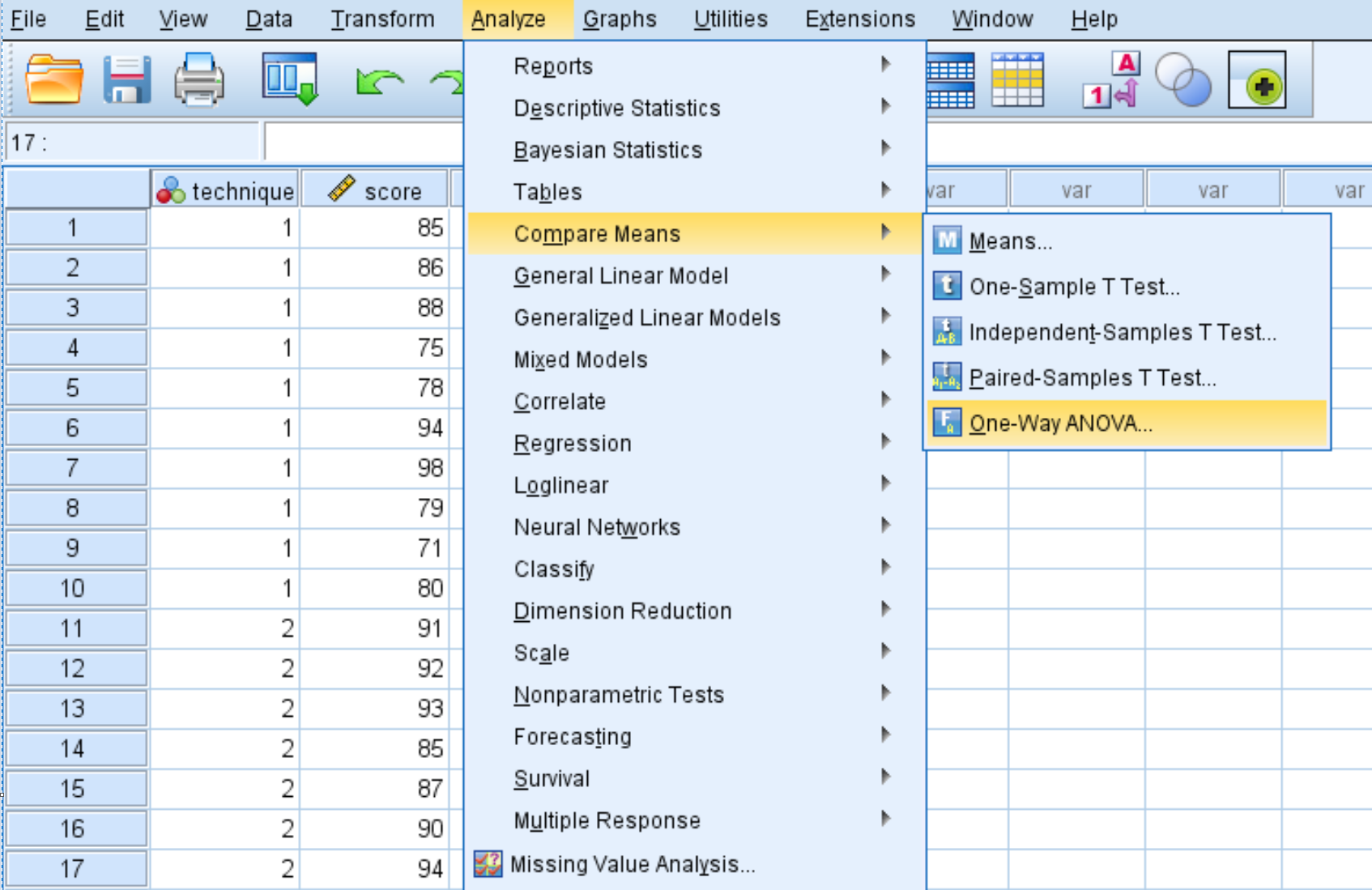
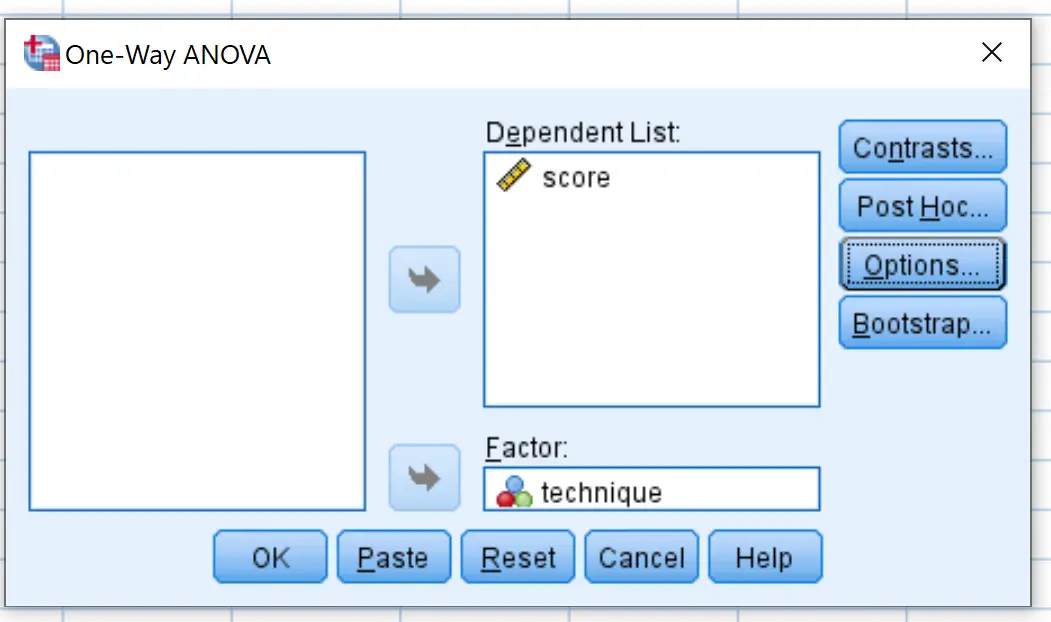
Dans la nouvelle fenêtre qui apparaît, placez le score variable dans la case intitulée Liste dépendante et la technique variable dans la case intitulée Facteur.

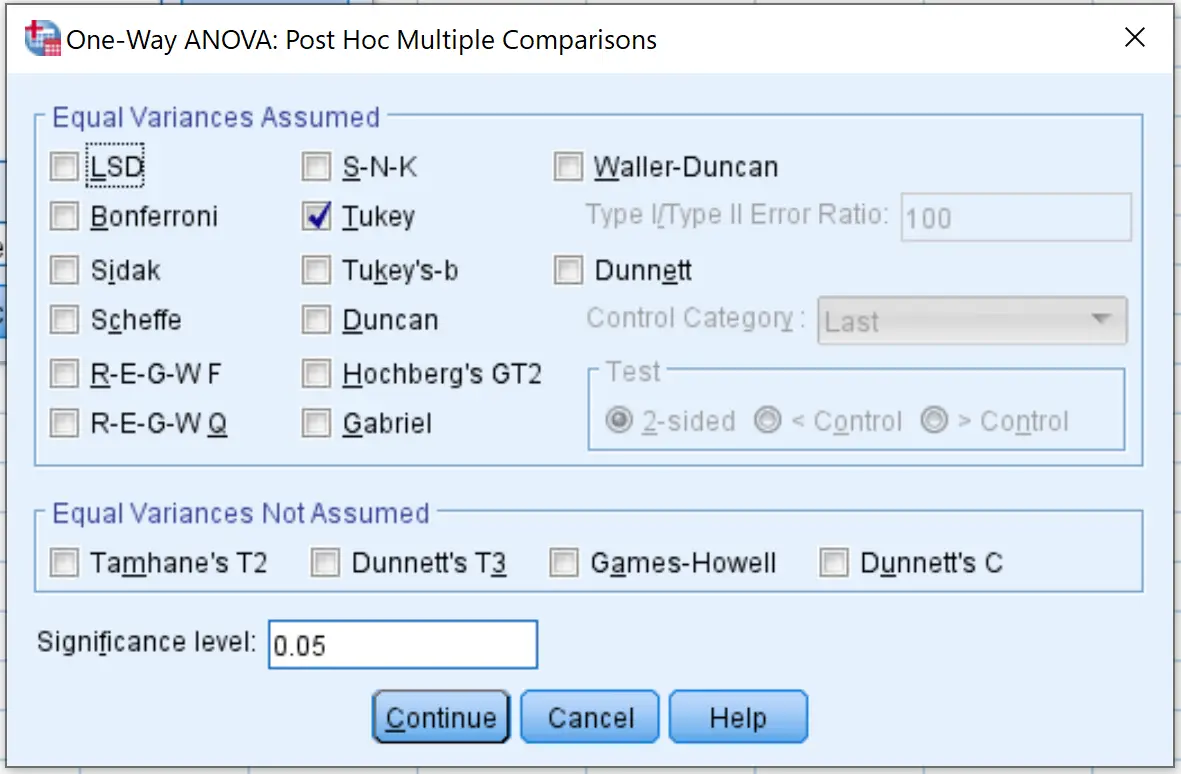
Cliquez ensuite sur Post Hoc et cochez la case à côté de Tukey . Cliquez ensuite sur Continuer .

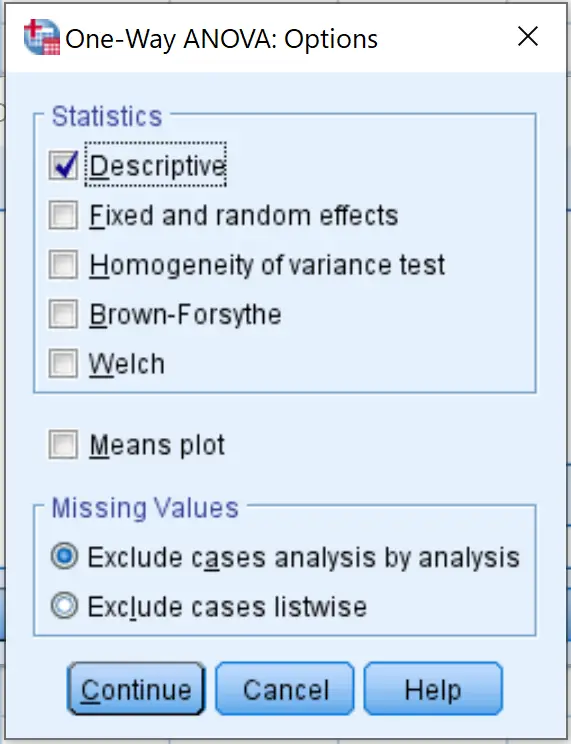
Cliquez ensuite sur Options et cochez la case à côté de Descriptive . Cliquez ensuite sur Continuer .

Enfin, cliquez sur OK .

Étape 3 : Interprétez le résultat.

Une fois que vous avez cliqué sur OK , les résultats de l’ANOVA unidirectionnelle apparaîtront. Voici comment interpréter le résultat :

Tableau descriptif

Ce tableau affiche des statistiques descriptives pour chacun des trois groupes de notre ensemble de données.

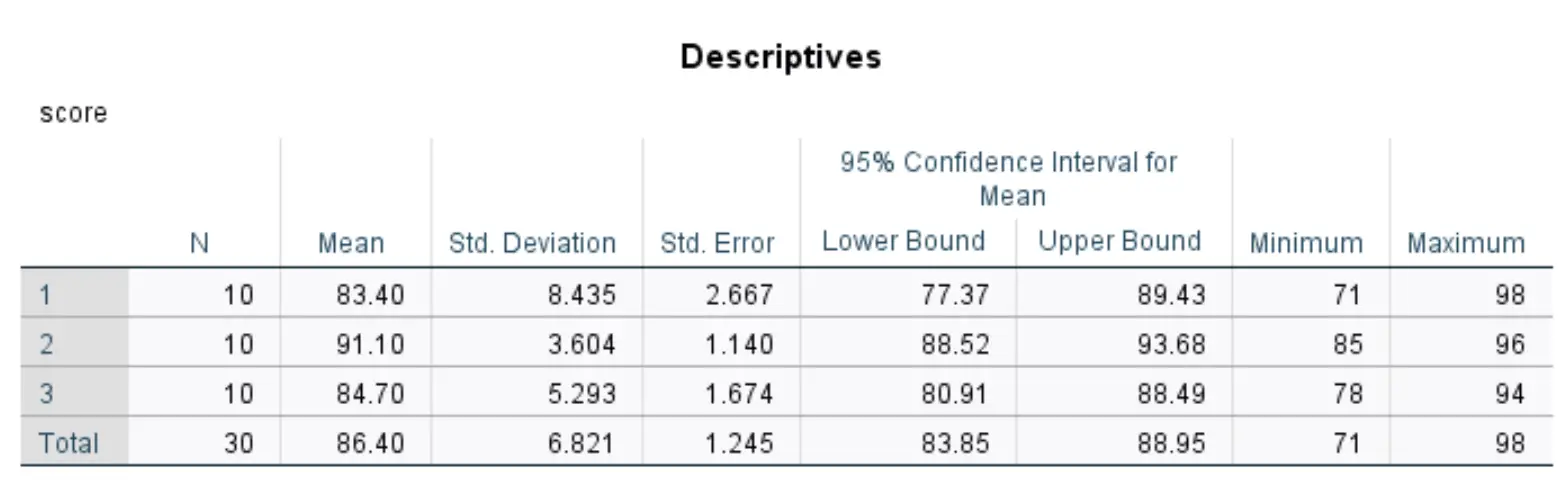
Les chiffres les plus pertinents incluent :

• N : Le nombre d’élèves dans chaque groupe.
• Moyenne : le score moyen au test pour chaque groupe.
• Norme. Écart : écart type des résultats des tests pour chaque groupe.

Tableau ANOVA

Ce tableau affiche les résultats de l’ANOVA unidirectionnelle :

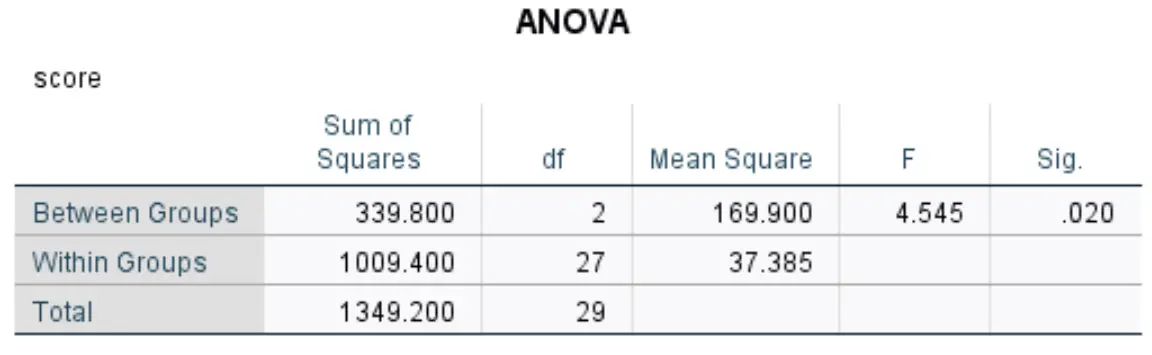
Les chiffres les plus pertinents incluent :

• F : La statistique F globale.
• Sig : La valeur p qui correspond à la statistique F (4,545) avec le numérateur df (2) et le dénominateur df (27). Dans ce cas, la valeur p s’avère être de 0,020 .

Rappelons qu’une ANOVA unidirectionnelle utilise les hypothèses nulles et alternatives suivantes :

• H ₀ (hypothèse nulle) : μ ₁ = μ ₂ = μ ₃ = … = μ _k (toutes les moyennes de population sont égales)
• H _A (hypothèse alternative) : au moins une moyenne de population est différente   du reste

Étant donné que la valeur p du tableau ANOVA est inférieure à 0,05, nous disposons de preuves suffisantes pour rejeter l’hypothèse nulle et conclure qu’au moins une des moyennes du groupe est différente des autres.

Pour savoir exactement quelles moyennes de groupe diffèrent les unes des autres, nous pouvons nous référer au dernier tableau du résultat ANOVA.

Tableau de comparaisons multiples

Ce tableau affiche les comparaisons multiples post-hoc de Tukey entre chacun des trois groupes. Nous nous intéressons principalement au Sig. colonne, qui affiche les valeurs p pour les différences de moyennes entre chaque groupe :

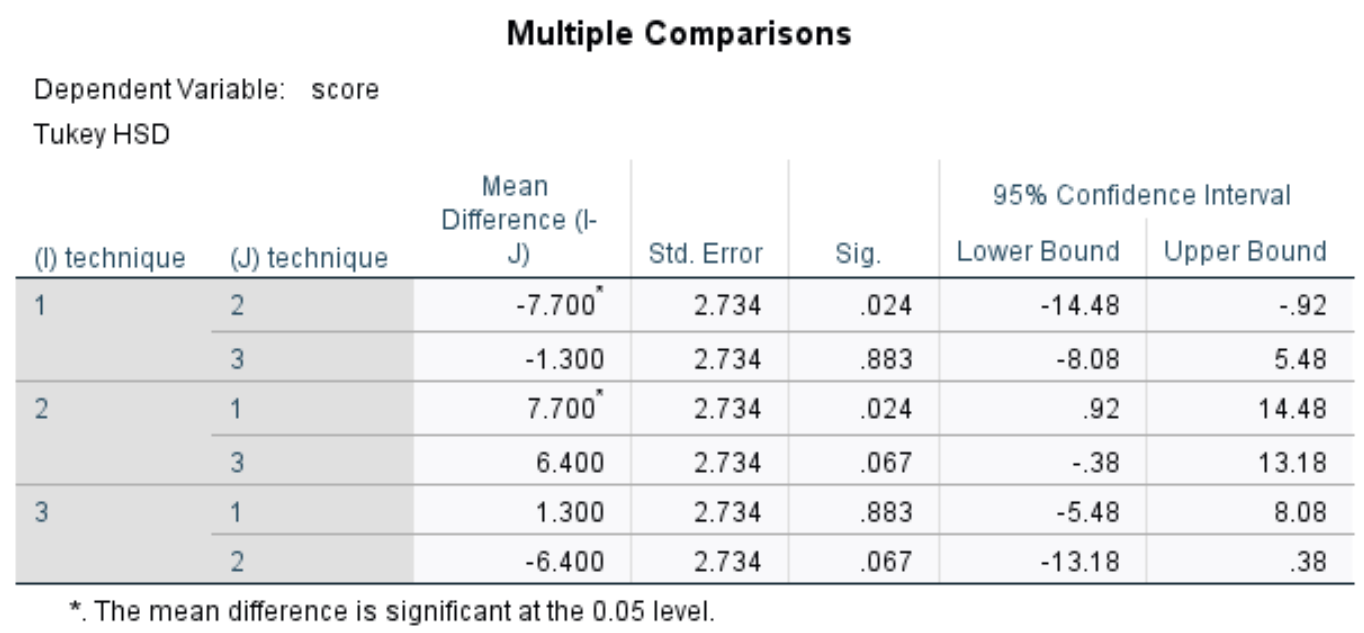
Dans le tableau, nous pouvons voir les valeurs p pour les comparaisons suivantes :

• Technique 1 contre 2 : | valeur p = 0,024
• Technique 1 contre 3 | valeur p = 0,883
• Technique 2 contre 3 | valeur p = 0,067

La seule comparaison de groupe ayant une valeur p inférieure à 0,05 concerne la technique 1 et la technique 2.

Cela nous indique qu’il existe une différence statistiquement significative dans les résultats moyens aux tests entre les étudiants qui ont utilisé la technique 1 et ceux qui ont utilisé la technique 2.

Cependant, il n’y a pas de différence statistiquement significative entre les techniques 1 et 3, ni entre les techniques 2 et 3.

Étape 4 : Rapportez les résultats.

Enfin, nous pouvons rapporter les résultats de l’ANOVA unidirectionnelle. Voici un exemple de la façon de procéder :

Une ANOVA unidirectionnelle a été réalisée pour déterminer si trois techniques d’étude différentes conduisaient à des résultats de test différents.

Au total, 10 étudiants ont utilisé chacune des trois techniques d’étude pendant un mois avant de passer tous le même test.

Une ANOVA unidirectionnelle a révélé qu’il existait une différence statistiquement significative dans les résultats des tests entre au moins deux groupes (F (2, 27) = 4,545, p = 0,020).

Le test de Tukey pour les comparaisons multiples a révélé que les résultats moyens aux tests étaient significativement différents entre les étudiants qui utilisaient la technique 1 et la technique 2 (p = 0,024, IC à 95 % = [-14,48, -0,92]).

Il n’y avait pas de différence statistiquement significative entre les scores des techniques 1 et 3 (p = 0,883) ou entre les scores des techniques 2 et 3 (p = 0,067).