Comment créer et interpréter des tracés Q-Q dans SPSS

Un tracé QQ , abréviation de « quantile-quantile », est souvent utilisé pour évaluer si une variable est normalement distribuée ou non.

Ce didacticiel explique comment créer et interpréter un tracé QQ dans SPSS.

Exemple : tracé QQ dans SPSS

Supposons que nous ayons l’ensemble de données suivant dans SPSS qui affiche les points par match pour 25 joueurs de basket différents :

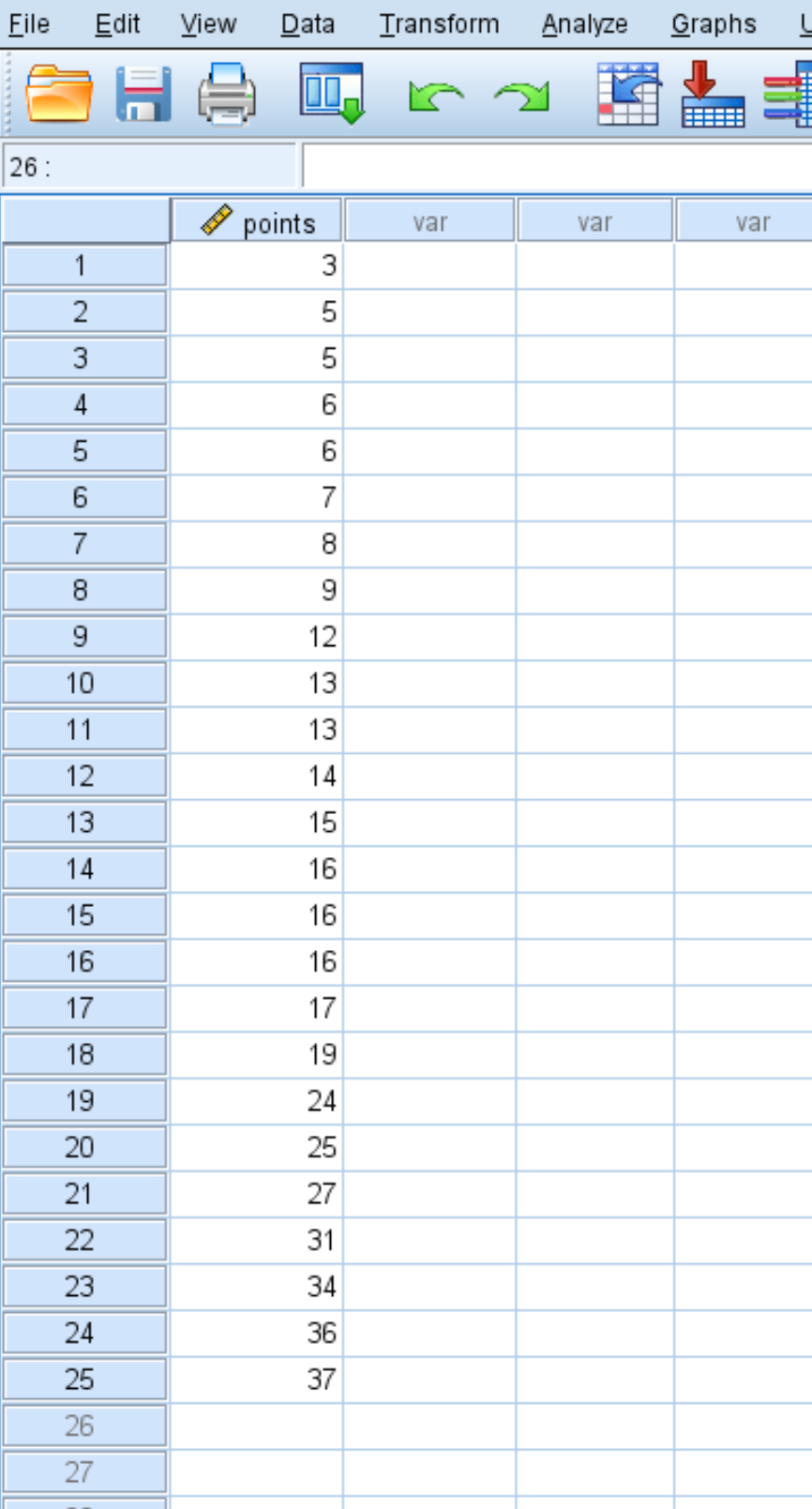
Nous pouvons utiliser les étapes suivantes dans SPSS pour créer un tracé QQ afin de déterminer si les points variables sont normalement distribués ou non.

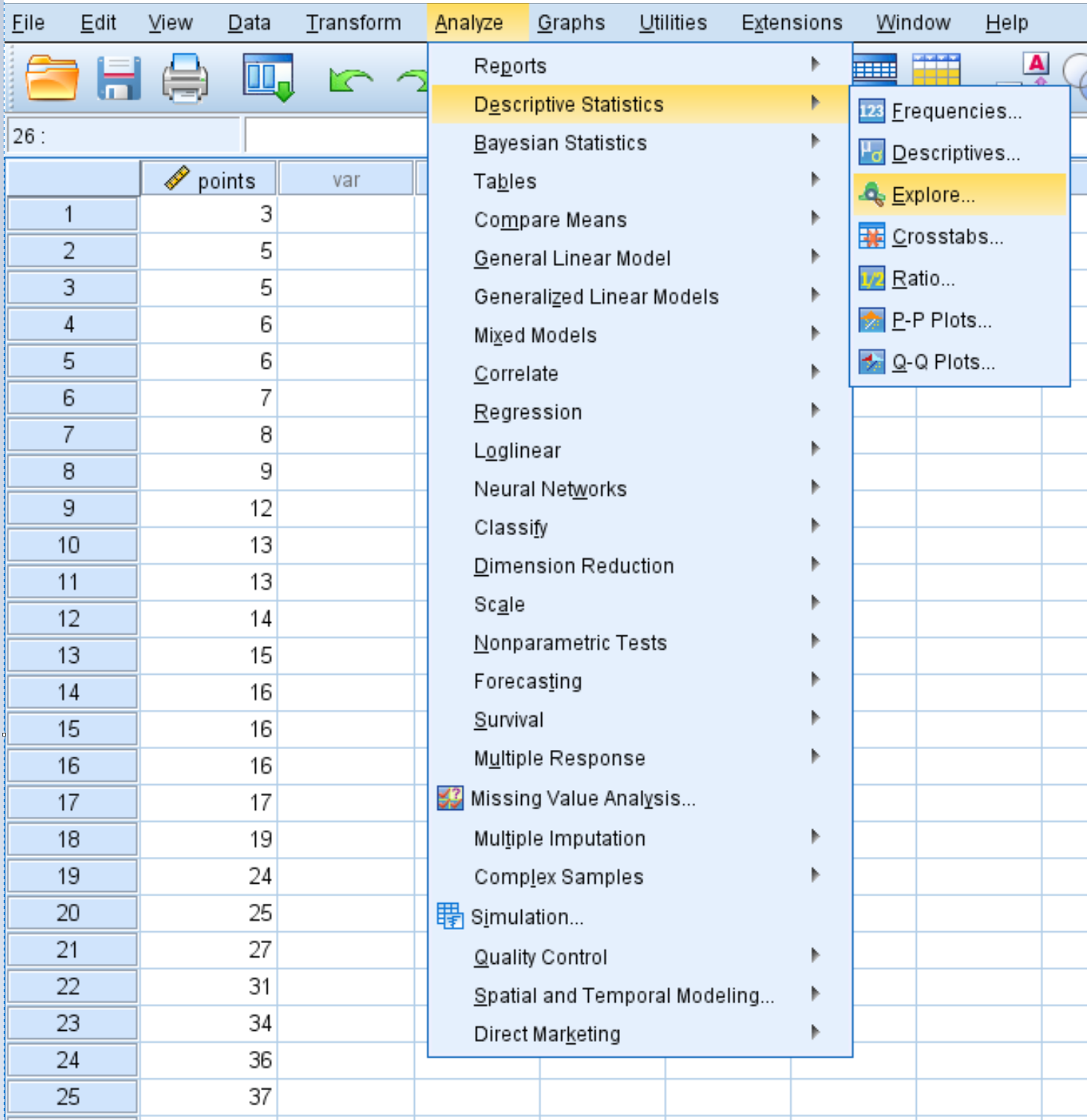
Étape 1 : Choisissez l’option Explorer.

Cliquez sur l’onglet Analyser , puis Statistiques descriptives , puis Explorer :

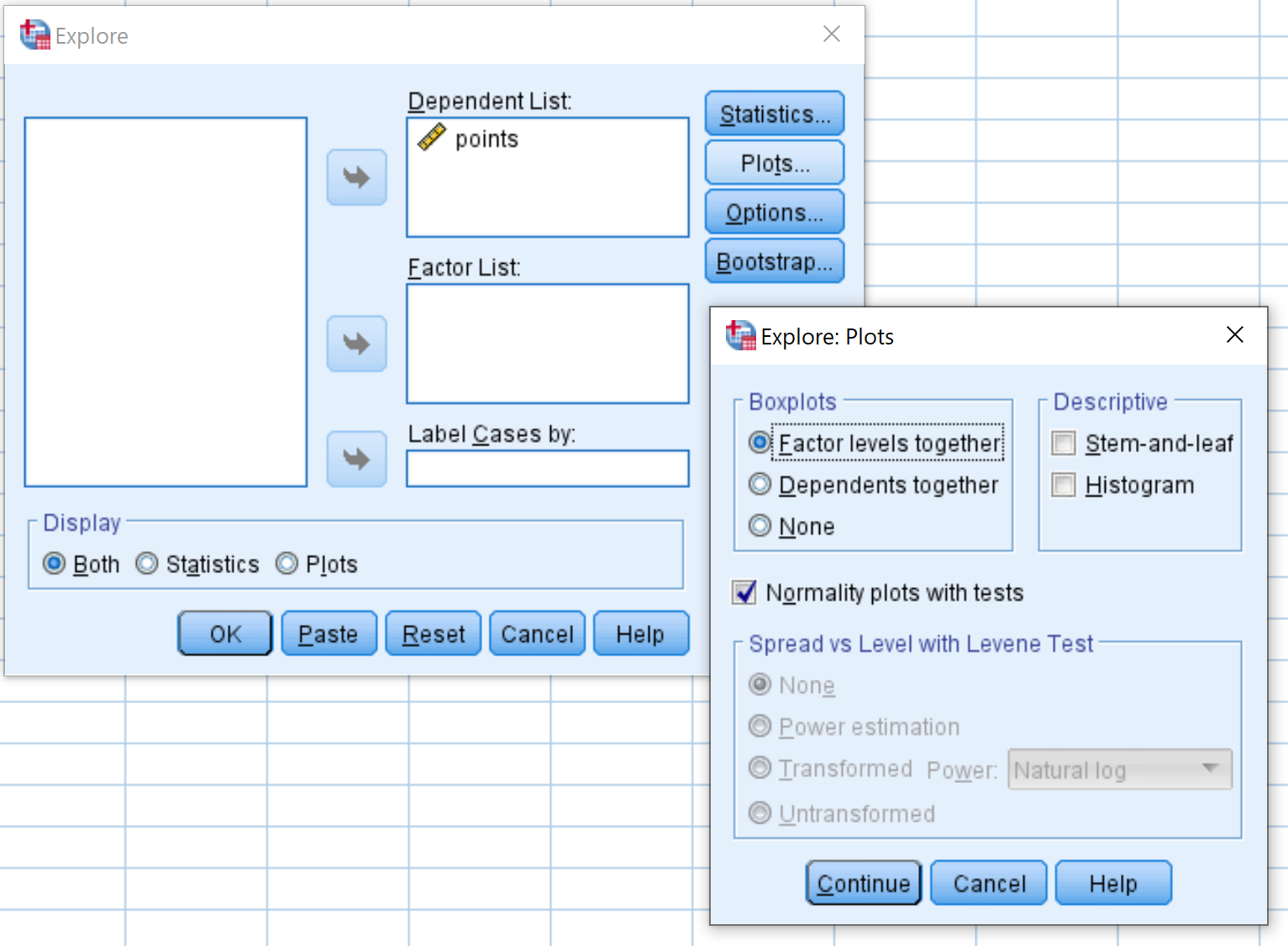
Étape 2 : Créez le tracé QQ.

Faites glisser les points variables dans la zone intitulée Liste dépendante. Cliquez ensuite sur le bouton intitulé Tracés et assurez-vous que la case est cochée à côté de Tracés de normalité avec tests . Cliquez ensuite sur Continuer . Cliquez ensuite sur OK .

Étape 3 : Interprétez le tracé QQ.

Une fois que vous avez cliqué sur OK , le tracé QQ suivant s’affichera :

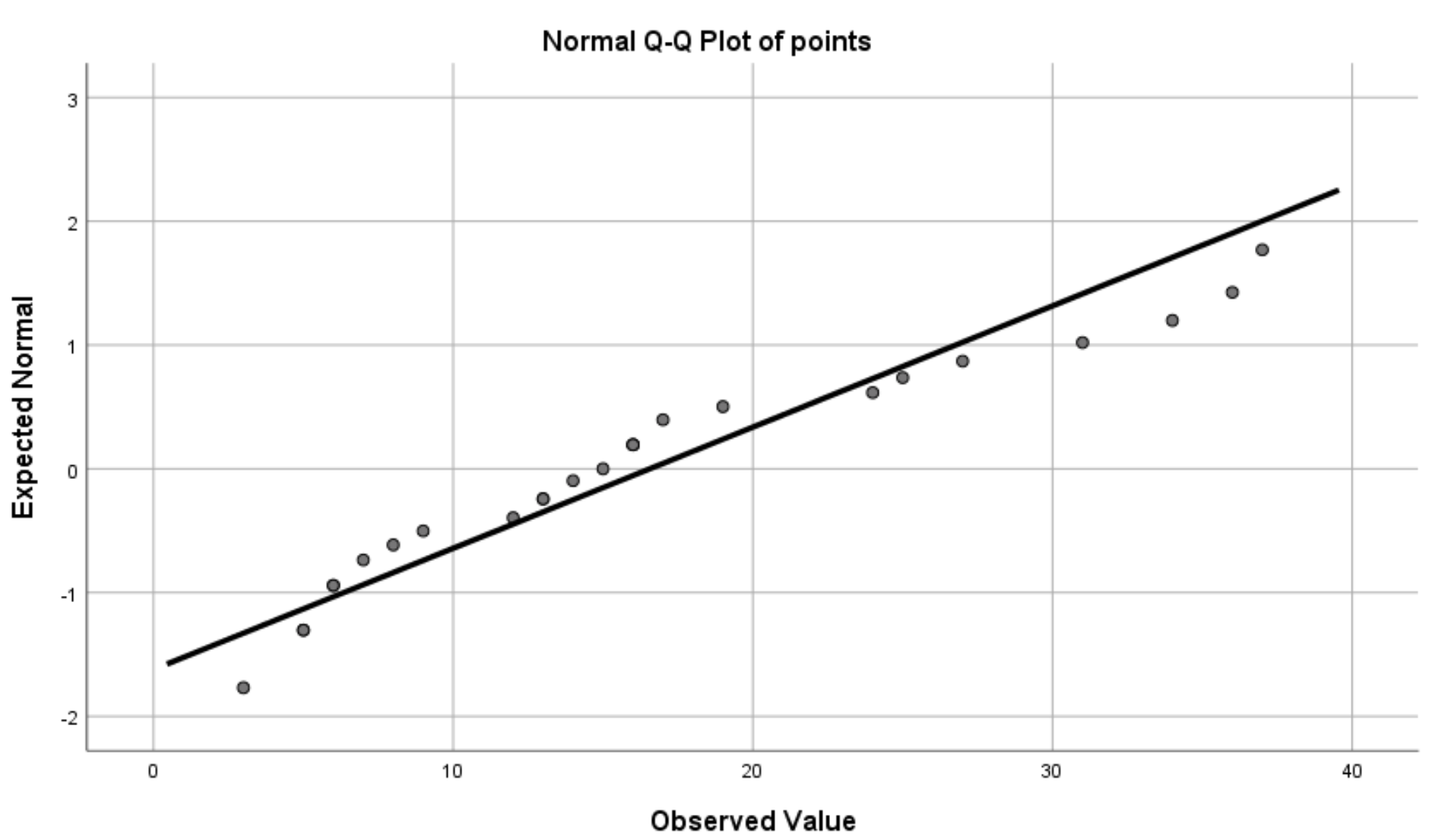
L’idée derrière un tracé QQ est simple : si les résidus suivent une ligne à peu près droite à un angle de 45 degrés, alors les résidus sont à peu près normalement distribués.

Nous pouvons voir dans notre graphique QQ ci-dessus que les résidus ont tendance à s’écarter un peu de la ligne de 45 degrés, en particulier aux extrémités, ce qui pourrait indiquer qu’ils ne sont pas normalement distribués.

Bien qu’un tracé QQ ne soit pas un test statistique formel, il offre un moyen simple de vérifier visuellement si les résidus sont normalement distribués ou non.

Pour deux tests statistiques formels, reportez-vous aux valeurs p du test de Kolmogorov-Smirnov et du test de Shapiro-Wilk affichées au-dessus du tracé QQ :

• Valeur P du test de normalité de Kolmogorov-Smirnov : 0,086
• Valeur P du test de normalité de Shapiro-Wilk : 0,042

Étant donné que ces deux valeurs sont proches de 0,05, cela indique que les points variables peuvent ne pas être distribués normalement.