Comment effectuer une régression logistique dans SPSS

La régression logistique est une méthode que nous utilisons pour ajuster un modèle de régression lorsque la variable de réponse est binaire.

Ce didacticiel explique comment effectuer une régression logistique dans SPSS.

Exemple : régression logistique dans SPSS

Utilisez les étapes suivantes pour effectuer une régression logistique dans SPSS pour un ensemble de données indiquant si des joueurs de basket-ball universitaire ont été repêchés ou non dans la NBA (repêchage : 0 = non, 1 = oui) en fonction de leur moyenne de points par match et de leur niveau de division.

Étape 1 : Saisissez les données.

Tout d’abord, saisissez les données suivantes :

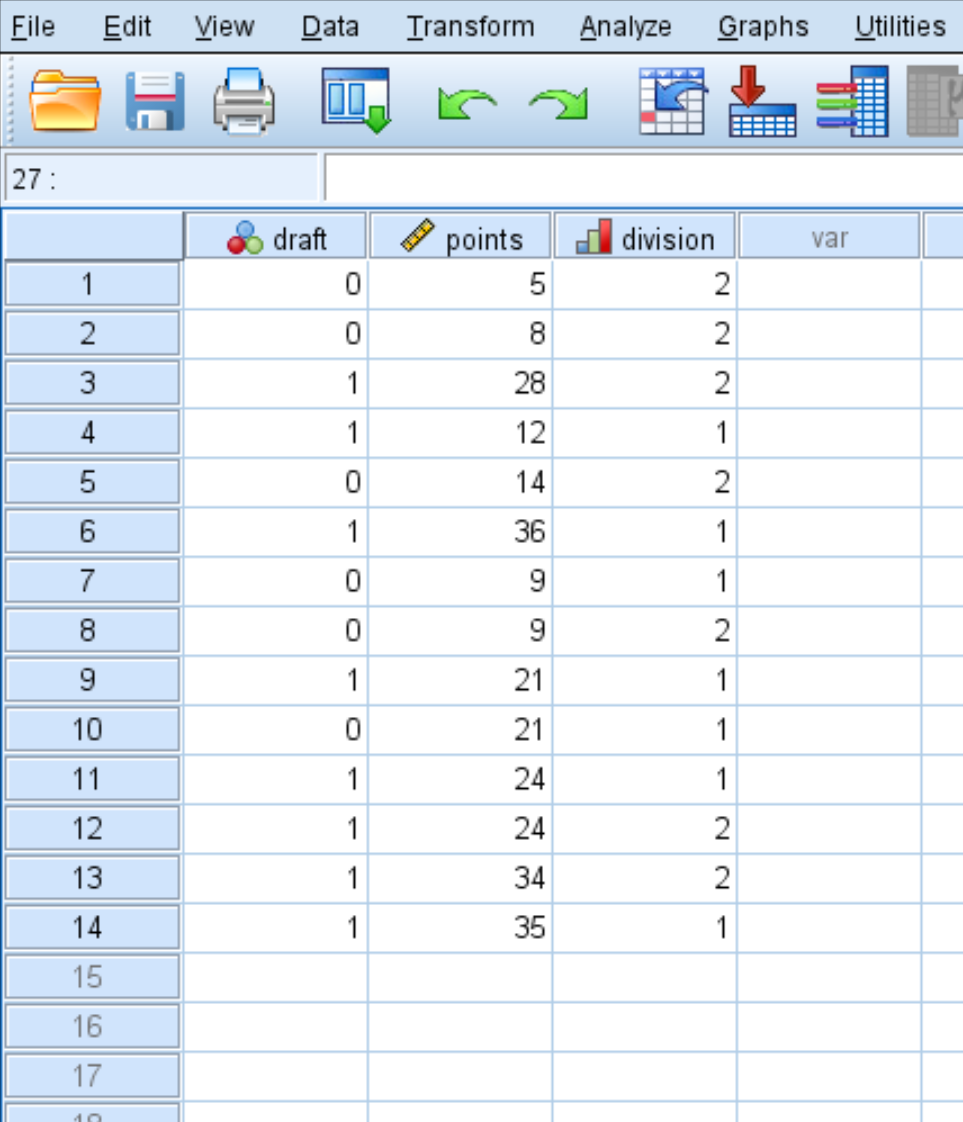
Étape 2 : Effectuez une régression logistique.

Cliquez sur l’onglet Analyser , puis Régression , puis Régression Logistique Binaire :

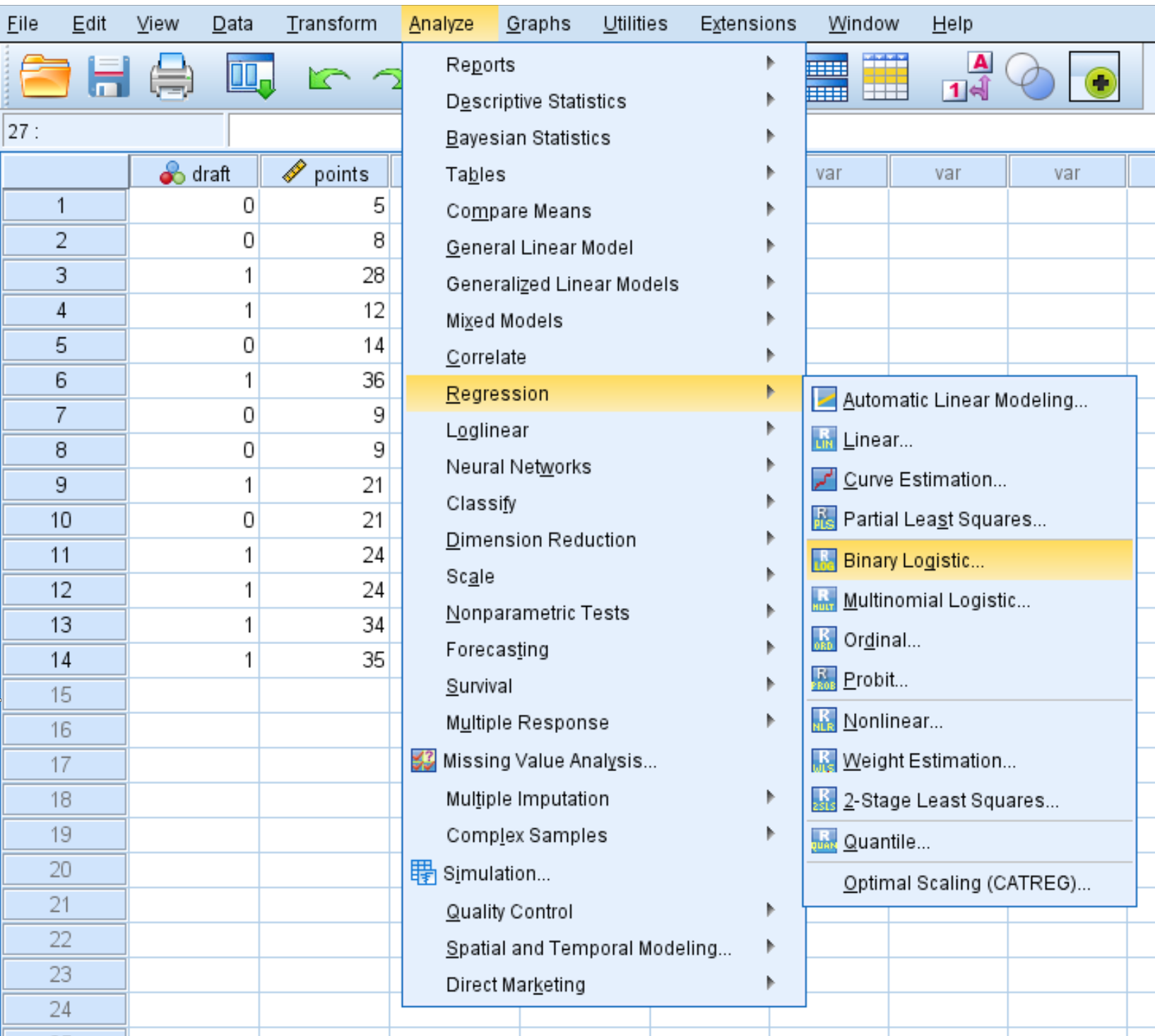
Dans la nouvelle fenêtre qui apparaît, faites glisser le projet de variable de réponse binaire dans la zone intitulée Dépendant. Faites ensuite glisser les deux points et la division des variables prédictives dans la case intitulée Bloc 1 sur 1. Laissez la méthode définie sur Entrée. Cliquez ensuite sur OK .

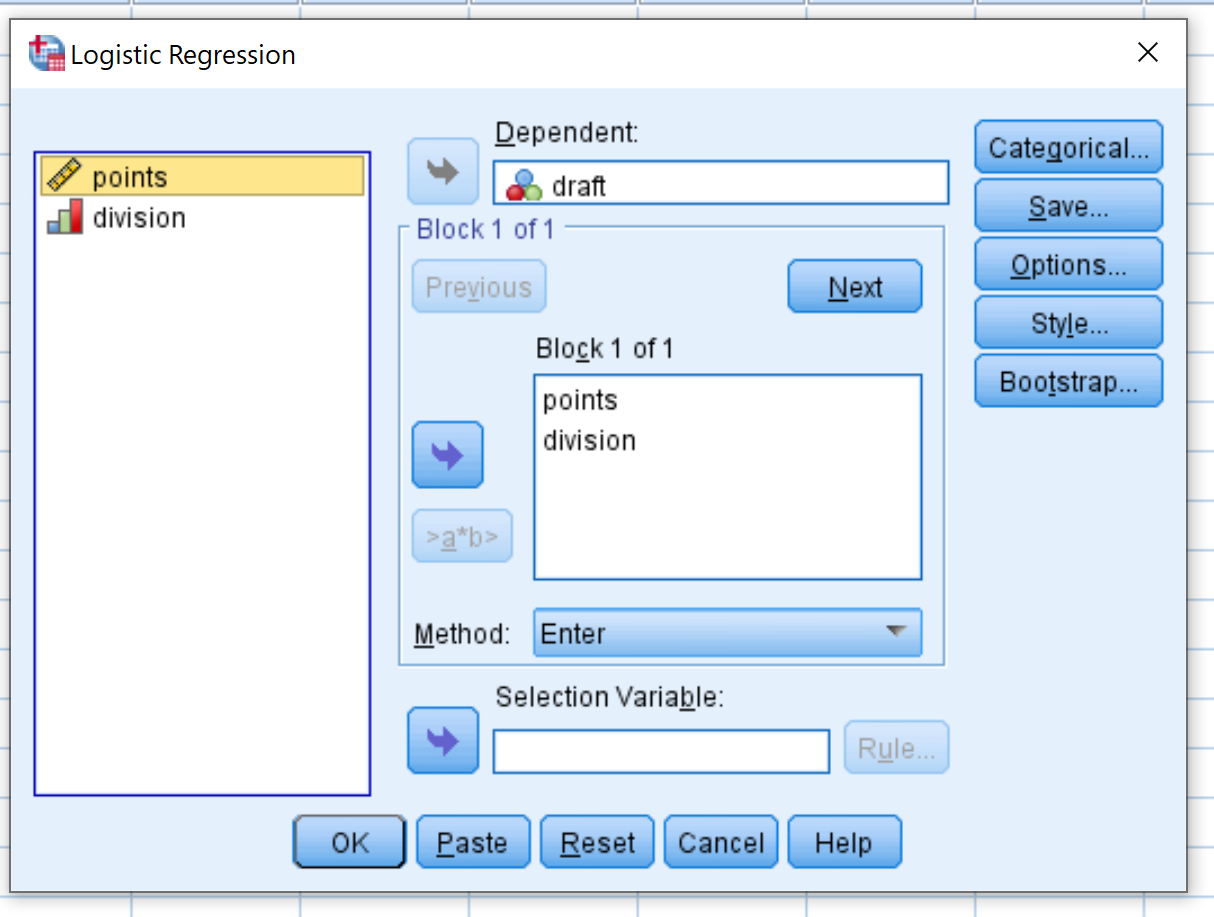
Étape 3. Interprétez le résultat.

Une fois que vous avez cliqué sur OK , le résultat de la régression logistique apparaîtra :

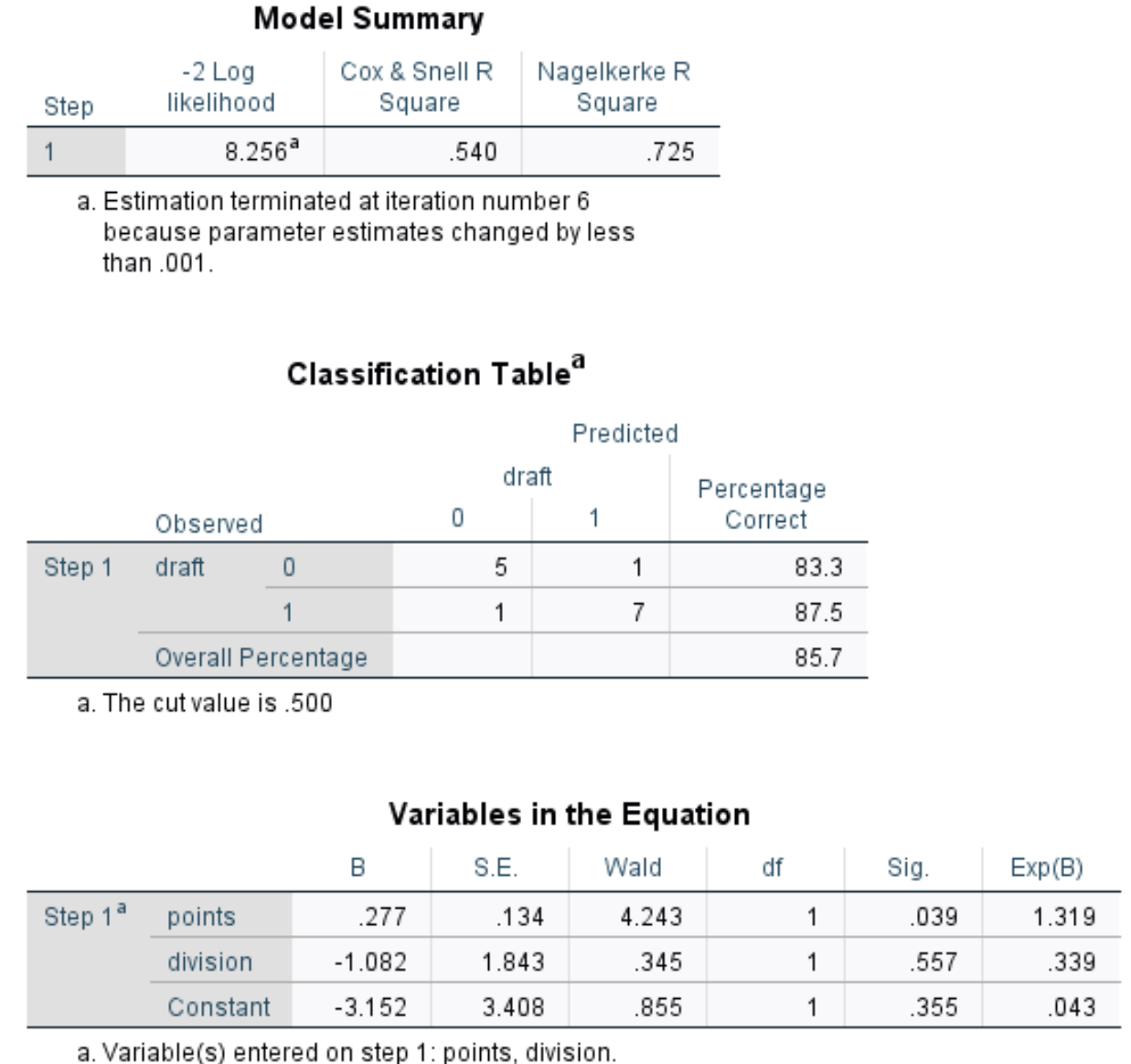
Voici comment interpréter le résultat :

Résumé du modèle : La métrique la plus utile dans ce tableau est le Nagelkerke R Square, qui nous indique le pourcentage de variation de la variable de réponse qui peut être expliqué par les variables prédictives. Dans ce cas, les points et la division peuvent expliquer 72,5% de la variabilité du repêchage.

Tableau de classification : la mesure la plus utile de ce tableau est le pourcentage global, qui nous indique le pourcentage d’observations que le modèle a pu classer correctement. Dans ce cas, le modèle de régression logistique a pu prédire correctement le résultat du repêchage de 85,7 % des joueurs.

Variables dans l’équation : ce dernier tableau nous fournit plusieurs mesures utiles, notamment :

• Wald : statistique du test de Wald pour chaque variable prédictive, qui est utilisée pour déterminer si chaque variable prédictive est statistiquement significative ou non.
• Sig : la valeur p qui correspond à la statistique du test de Wald pour chaque variable prédictive. Nous voyons que la valeur p pour les points est de 0,039 et la valeur p pour la division est de 0,557.
• Exp(B) : le rapport de cotes pour chaque variable prédictive. Cela nous indique le changement dans les chances qu’un joueur soit repêché, associé à une augmentation d’une unité d’une variable prédictive donnée. Par exemple, les chances qu’un joueur de la division 2 soit repêché ne représentent que 0,339 des chances qu’un joueur de la division 1 soit repêché. De même, chaque augmentation d’unité supplémentaire en points par match est associée à une augmentation de 1,319 des chances qu’un joueur soit repêché.

Nous pouvons ensuite utiliser les coefficients (les valeurs dans la colonne intitulée B) pour prédire la probabilité qu’un joueur donné soit repêché, en utilisant la formule suivante :

Probabilité = e ^{-3,152 + 0,277 (points) – 1,082 (division)} / (1+e ^{-3,152 + 0,277 (points) – 1,082 (division)} )

Par exemple, la probabilité qu’un joueur qui totalise en moyenne 20 points par match et qui joue en division 1 soit repêché peut être calculée comme suit :

Probabilité = e ^{-3,152 + 0,277(20) – 1,082(1)} / (1+e ^{-3,152 + 0,277(20) – 1,082(1)} ) = 0,787 .

Puisque cette probabilité est supérieure à 0,5, nous prédirions que ce joueur serait repêché.

Étape 4. Rapportez les résultats.

Enfin, nous souhaitons rapporter les résultats de notre régression logistique. Voici un exemple de la façon de procéder :

Une régression logistique a été réalisée pour déterminer comment les points par match et le niveau de division affectent la probabilité d’un joueur de basket-ball d’être repêché. Au total, 14 joueurs ont été utilisés dans l’analyse.

Le modèle a expliqué 72,5 % de la variation du résultat du projet et a correctement classé 85,7 % des cas.

Les chances qu’un joueur de la division 2 soit repêché n’étaient que de 0,339 des chances qu’un joueur de la division 1 soit repêché.

Chaque augmentation d’unité supplémentaire de points par match était associée à une augmentation de 1,319 des chances qu’un joueur soit repêché.