Comment effectuer un test d’ajustement du chi carré dans SPSS

Un test d’ajustement du chi carré est utilisé pour déterminer si une variable catégorielle suit ou non une distribution hypothétique.

Ce didacticiel explique comment effectuer un test d’ajustement du chi carré dans SPSS.

Exemple : test d’adéquation du chi carré dans SPSS

Un propriétaire de magasin affirme qu’un nombre égal de clients viennent dans son magasin chaque jour de la semaine. Pour tester cette hypothèse, un chercheur enregistre le nombre de clients qui viennent dans le magasin au cours d’une semaine donnée et trouve ce qui suit :

• Lundi : 50 clients
• Mardi : 60 clients
• Mercredi : 40 clients
• Jeudi : 47 clients
• Vendredi : 53 clients

Suivez les étapes suivantes pour effectuer un test d’ajustement du chi carré dans SPSS afin de déterminer si les données sont cohérentes avec l’affirmation du propriétaire du magasin.

Étape 1 : Saisissez les données.

Tout d’abord, saisissez les données dans SPSS au format suivant :

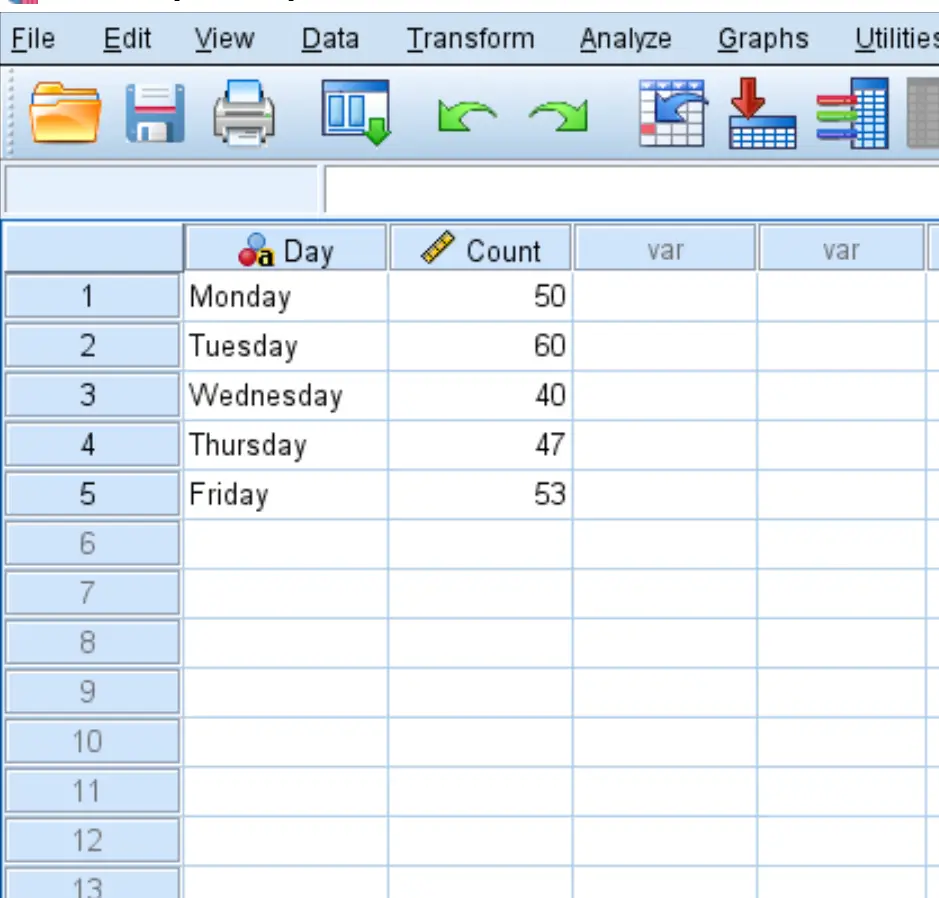
Étape 2 : Utilisez des cas pondérés.

Pour que le test fonctionne correctement, nous devons indiquer à SPSS que la variable « Jour » doit être pondérée par la variable « Nombre ».

Cliquez sur l’onglet Données , puis sur Pondérer les cas :

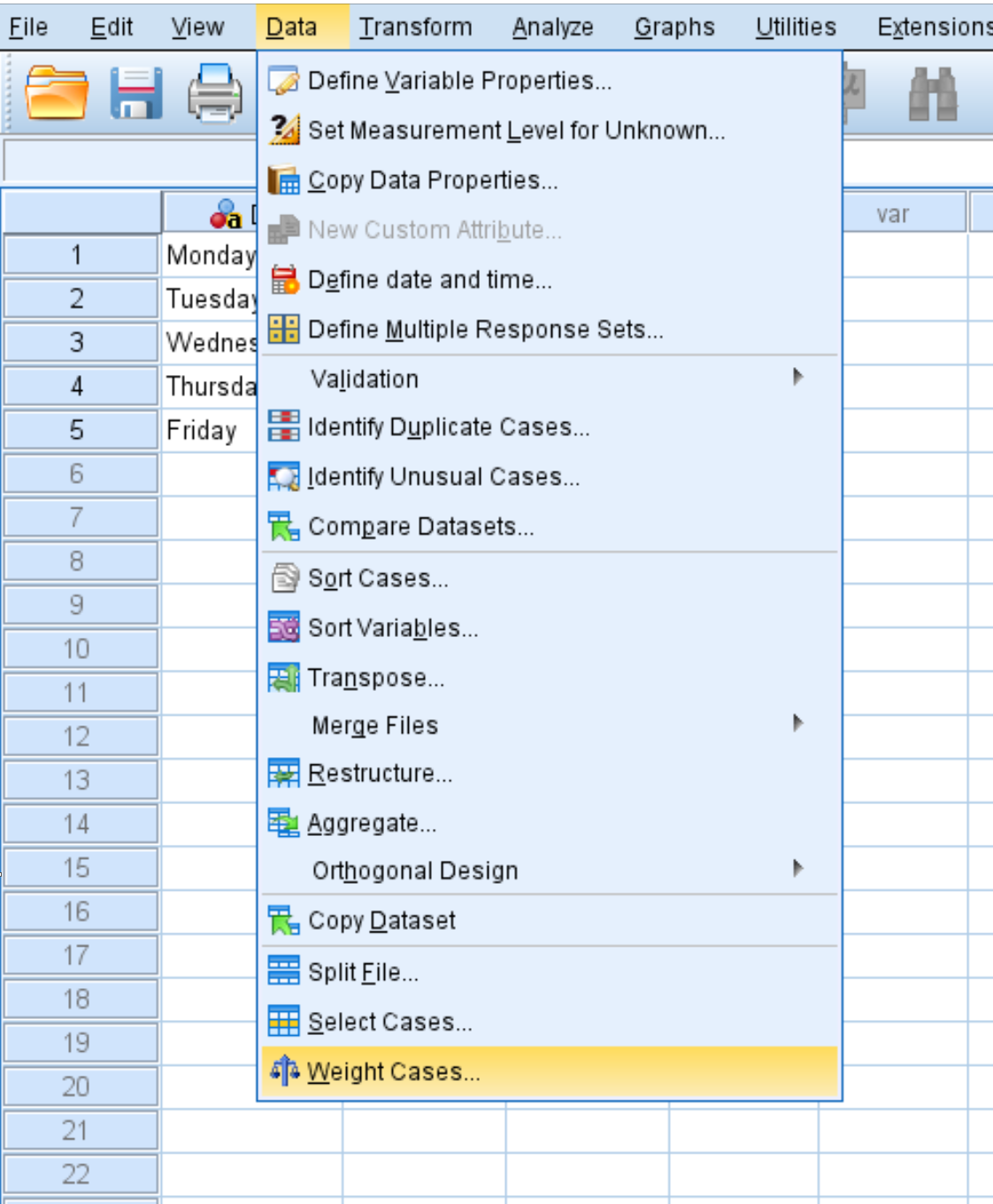
Dans la nouvelle fenêtre qui apparaît, faites glisser la variable Count dans la zone intitulée Test Variable List. Cliquez ensuite sur OK .

Étape 3 : Effectuez le test d’ajustement du chi carré.

Cliquez sur l’onglet Analyser , puis Tests non paramétriques , puis Boîtes de dialogue héritées , puis Chi carré :

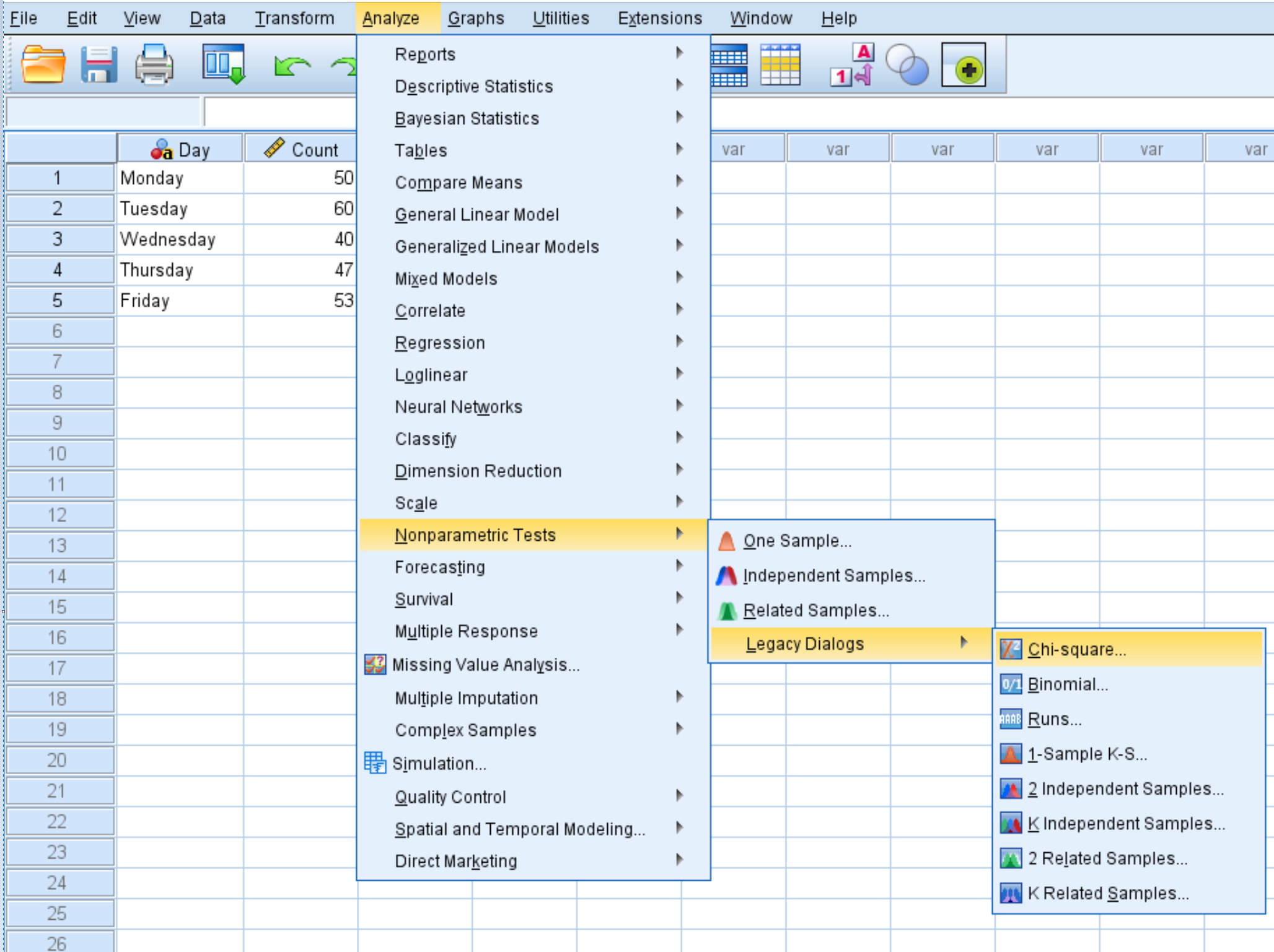
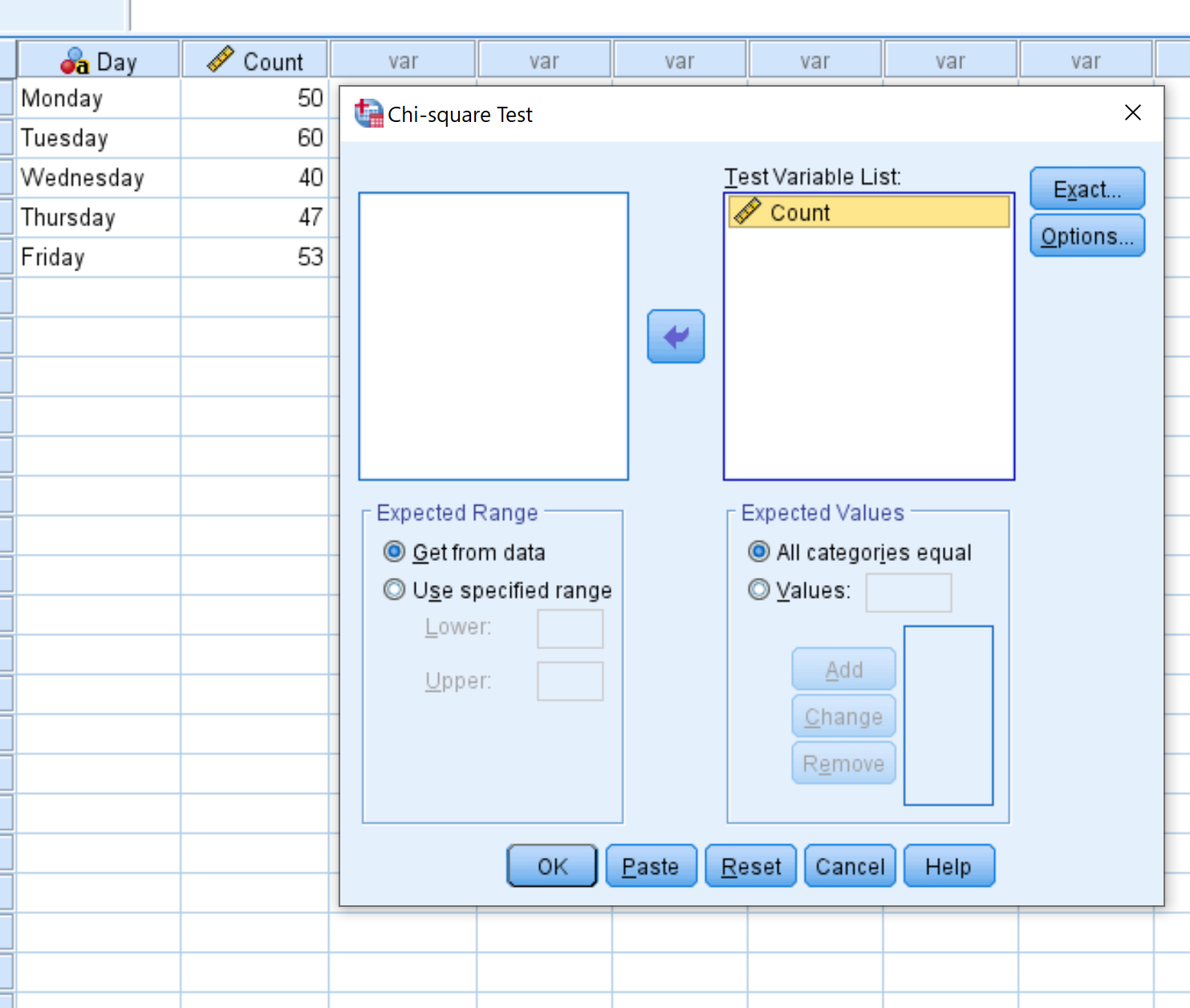
Dans la nouvelle fenêtre qui apparaît, faites glisser la variable Count dans la zone intitulée Test Variable List.

Laissez l’étiquette cochée à côté de Toutes les catégories égales puisque chacune de nos catégories (c’est-à-dire les jours de la semaine) a le même nombre attendu de visiteurs chaque jour. Cliquez ensuite sur OK .

Étape 4 : Interpréter les résultats .

Une fois que vous avez cliqué sur OK , les résultats du test d’ajustement du chi carré apparaîtront :

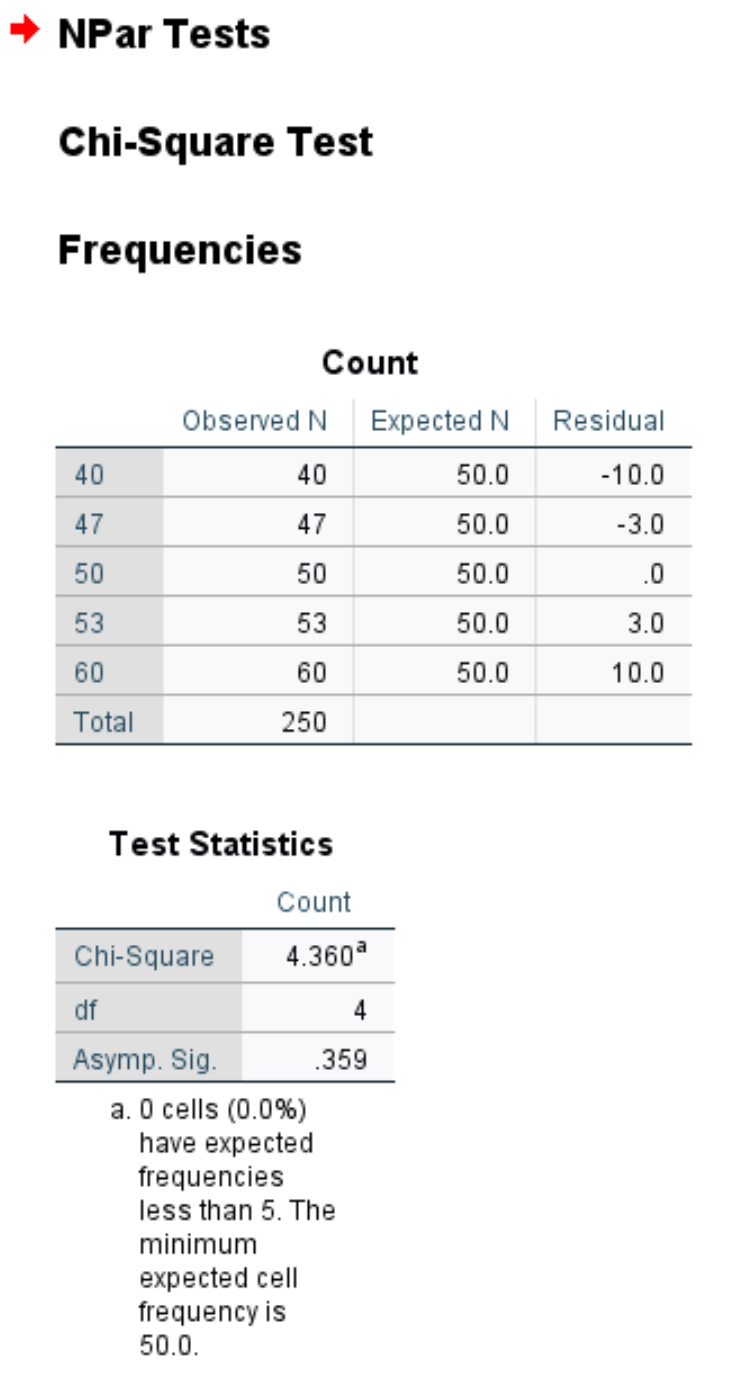
Le premier tableau montre le nombre de clients observé et attendu chaque jour de la semaine, ainsi que le résidu (c’est-à-dire la différence) entre observé et attendu.

Le deuxième tableau affiche les nombres suivants :

Chi carré : la statistique du test du chi carré, qui est de 4,36.

df : Les degrés de liberté, calculés comme #categories-1 = 5-1 = 4.

Asymp. Sig : La valeur p qui correspond à une valeur du Chi carré de 4,36 avec 4 degrés de liberté, qui est de 0,359. Cette valeur peut également être trouvée à l’aide du calculateur du score du chi carré vers la valeur P.

Puisque la valeur p (0,359) n’est pas inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle. Cela signifie que nous n’avons pas suffisamment de preuves pour affirmer que la véritable répartition des clients est différente de celle déclarée par le propriétaire du magasin.