Comment effectuer un test t sur un échantillon dans SPSS
Un test t sur un échantillon est utilisé pour tester si la moyenne d’une population est égale ou non à une certaine valeur.
Ce didacticiel explique comment effectuer un test t sur un échantillon dans SPSS.
Exemple : test t sur un échantillon dans SPSS
Un botaniste veut savoir si la hauteur moyenne d’une certaine espèce de plante est égale à 15 pouces. Elle prélève un échantillon aléatoire de 12 plantes et enregistre chacune de leurs hauteurs en pouces :
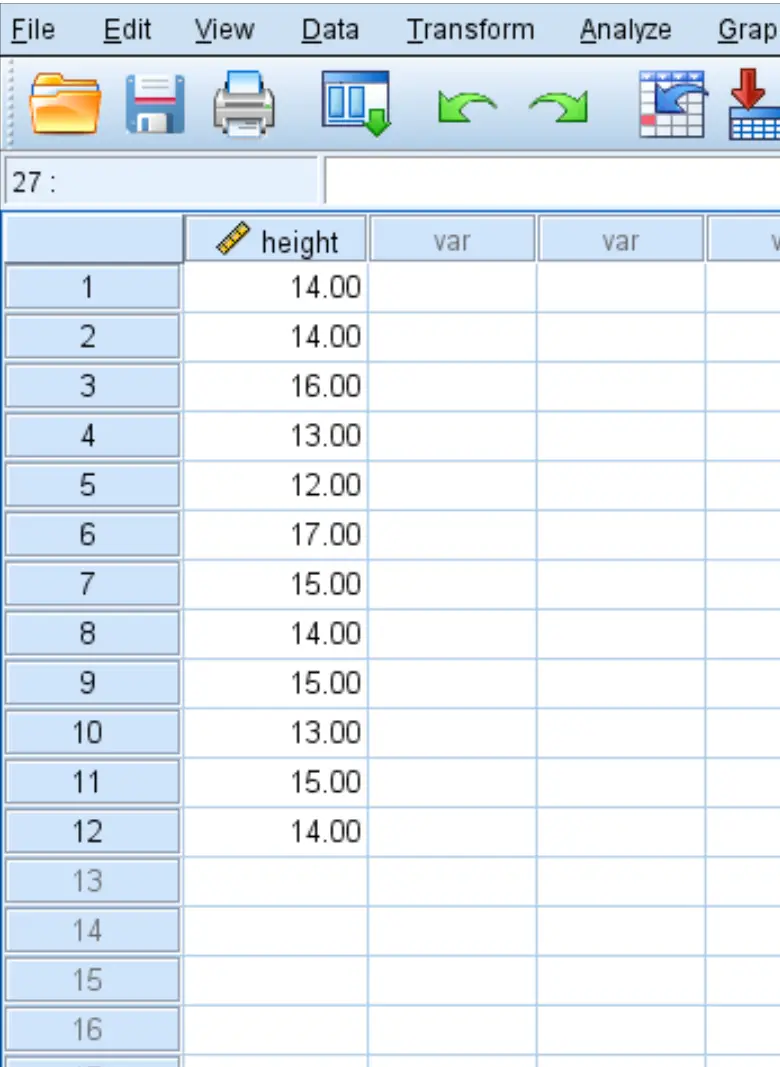
Utilisez les étapes suivantes pour effectuer un test t sur un échantillon afin de déterminer si la hauteur moyenne réelle de cette espèce de plante est égale à 15 pouces, sur la base des hypothèses nulles et alternatives suivantes :
- H 0 : μ = 15 (la moyenne réelle de la population est égale à 15 pouces)
- H 1 : μ ≠ 15 (la vraie moyenne de la population n’est pas égale à 15 pouces)
Utilisez un niveau de signification de α = 0,05.
Étape 1 : Choisissez l’option de test t sur un échantillon.
Cliquez sur l’onglet Analyser , puis sur Comparer les moyennes , puis sur Test T à un échantillon :
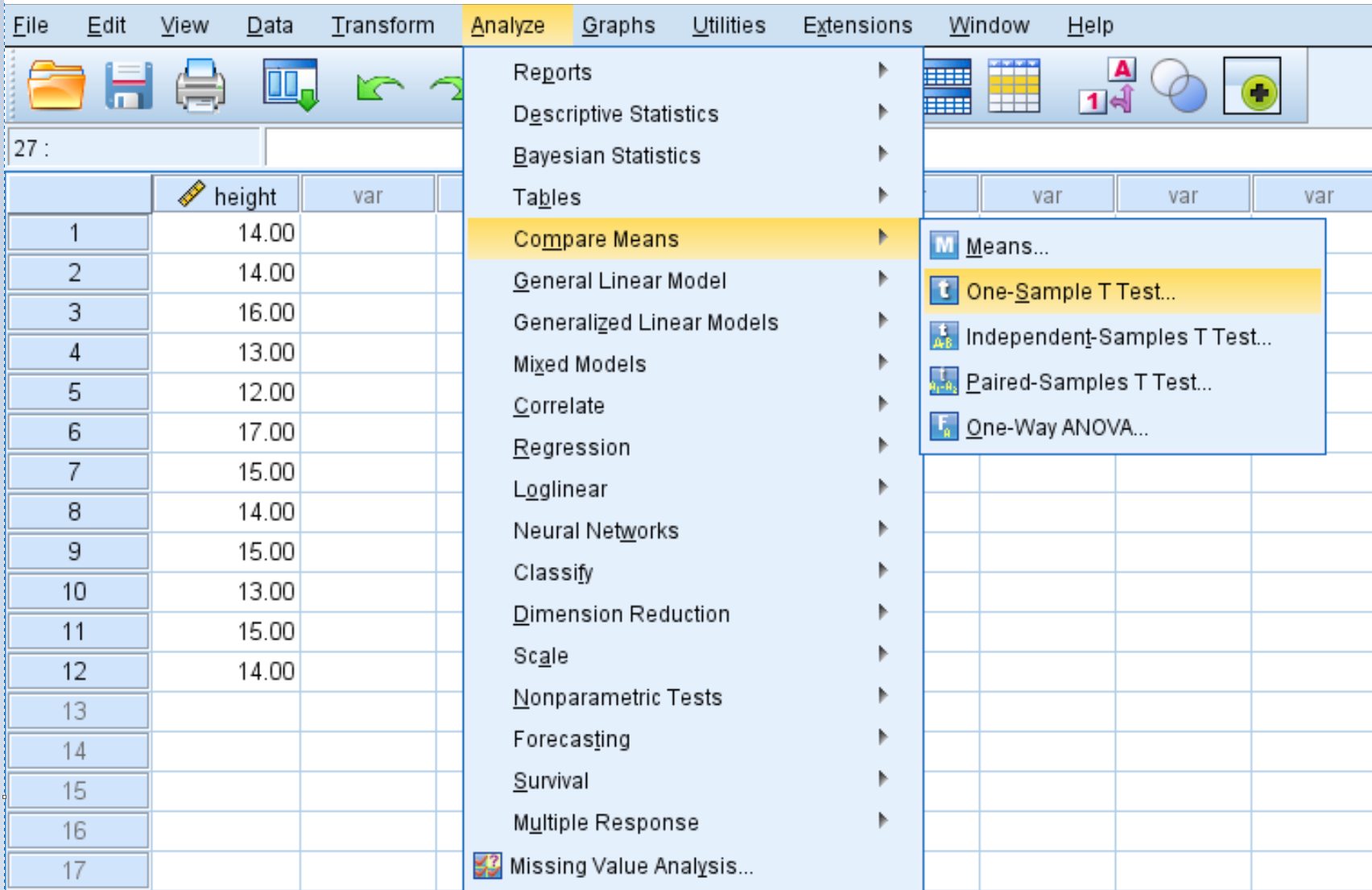
Étape 2 : Remplissez les valeurs nécessaires pour effectuer le test t sur un échantillon.
Une fois que vous avez cliqué sur One-Sample T Test , la fenêtre suivante apparaîtra :
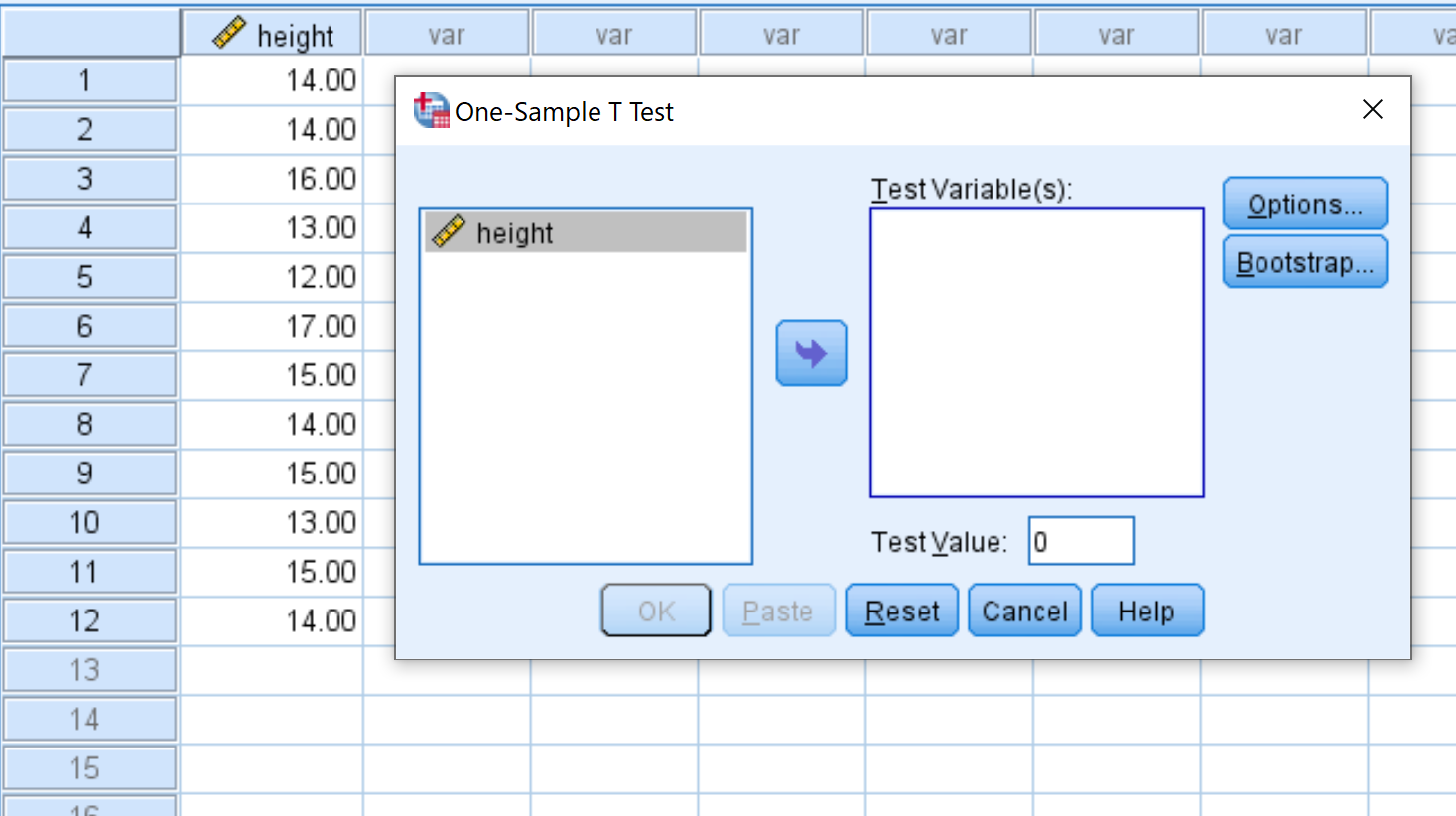
Faites glisser la hauteur de la variable dans la zone intitulée Variable(s) de test et modifiez la valeur de test sur 15. Cliquez ensuite sur OK .
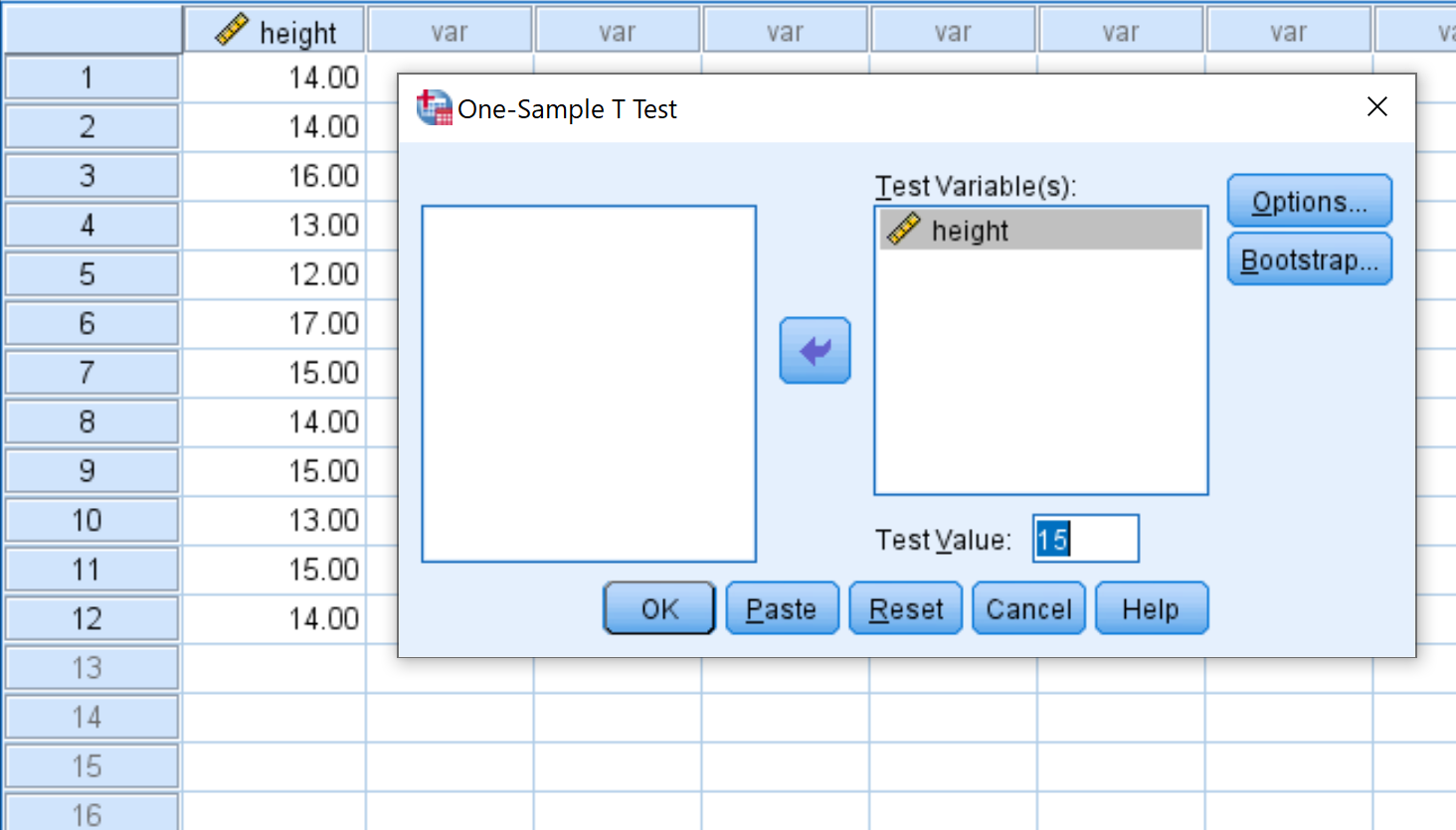
Étape 3 : Interprétez les résultats.
Une fois que vous avez cliqué sur OK , les résultats du test t sur un échantillon seront affichés :
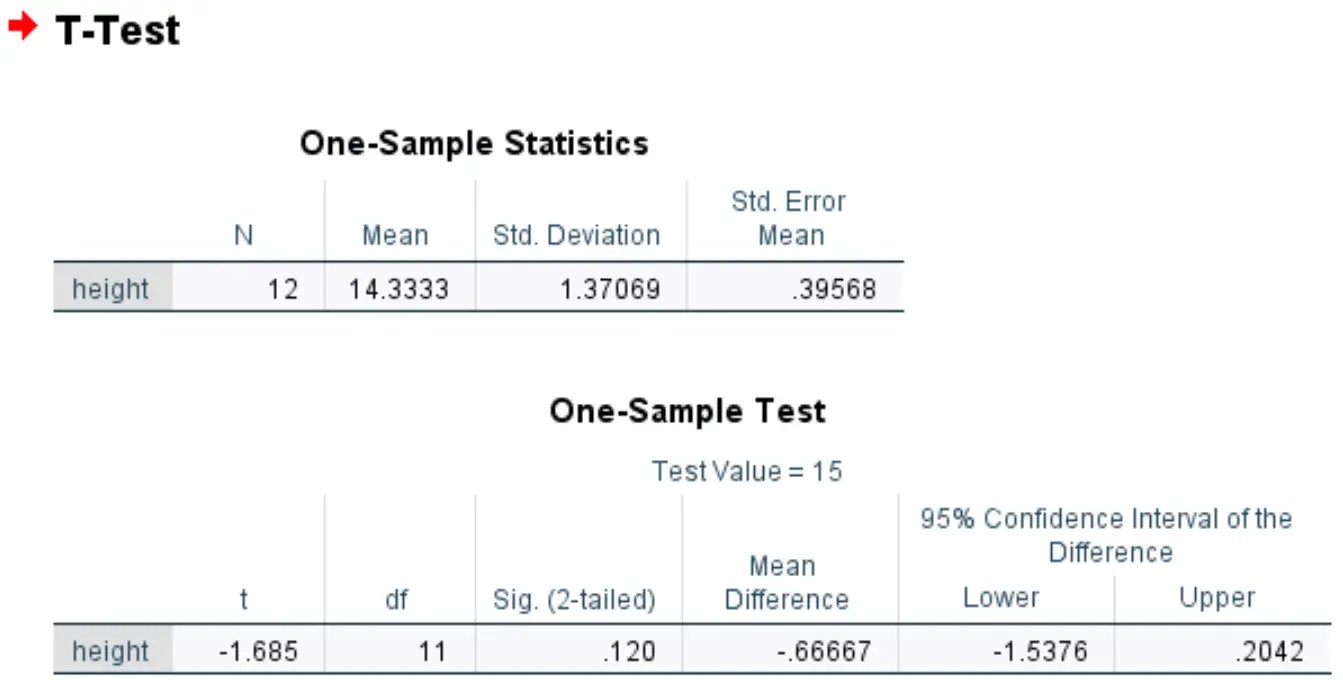
Le premier tableau affiche des statistiques récapitulatives pour la hauteur variable :
- N : La taille de l’échantillon
- Moyenne : la hauteur moyenne des plantes dans l’échantillon
- Norme. Écart : L’écart type de la hauteur des plantes dans l’échantillon.
- Norme. Moyenne d’erreur : l’erreur standard de la moyenne, calculée comme s/√n
Le deuxième tableau affiche les résultats du test t sur un échantillon :
- t : La statistique de test, calculée comme (x – μ) / (s/√n) = (14,3333-15) / (1,37/√12) = -1,685
- df : Les degrés de liberté, calculés comme n-1 = 12-1 = 11
- Sig. (bilatéral) : La valeur p bilatérale qui correspond à une valeur de -1,685 avec df=11
- Différence moyenne : la différence entre la moyenne de l’échantillon et la moyenne hypothétique
- IC à 95 % de la différence : intervalle de confiance à 95 % pour la vraie différence entre la moyenne de l’échantillon et la moyenne hypothétique.
Puisque la valeur p du test (0,120) n’est pas inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle. Nous n’avons pas suffisamment de preuves pour affirmer que la véritable hauteur moyenne de cette espèce de plante est différente de 15 pouces.
