Comment créer et interpréter des boîtes à moustaches dans SPSS

Une boîte à moustaches est utilisée pour visualiser le résumé en cinq chiffres d’un ensemble de données, qui comprend :

• Le minimum
• Le premier quartile
• La médiane
• Le troisième quartile
• Le maximum

Ce didacticiel explique comment créer et modifier des boîtes à moustaches dans SPSS.

Comment créer un diagramme en boîte unique dans SPSS

Supposons que nous ayons l’ensemble de données suivant qui montre la moyenne des points marqués par match par 16 joueurs de basket-ball d’une certaine équipe :

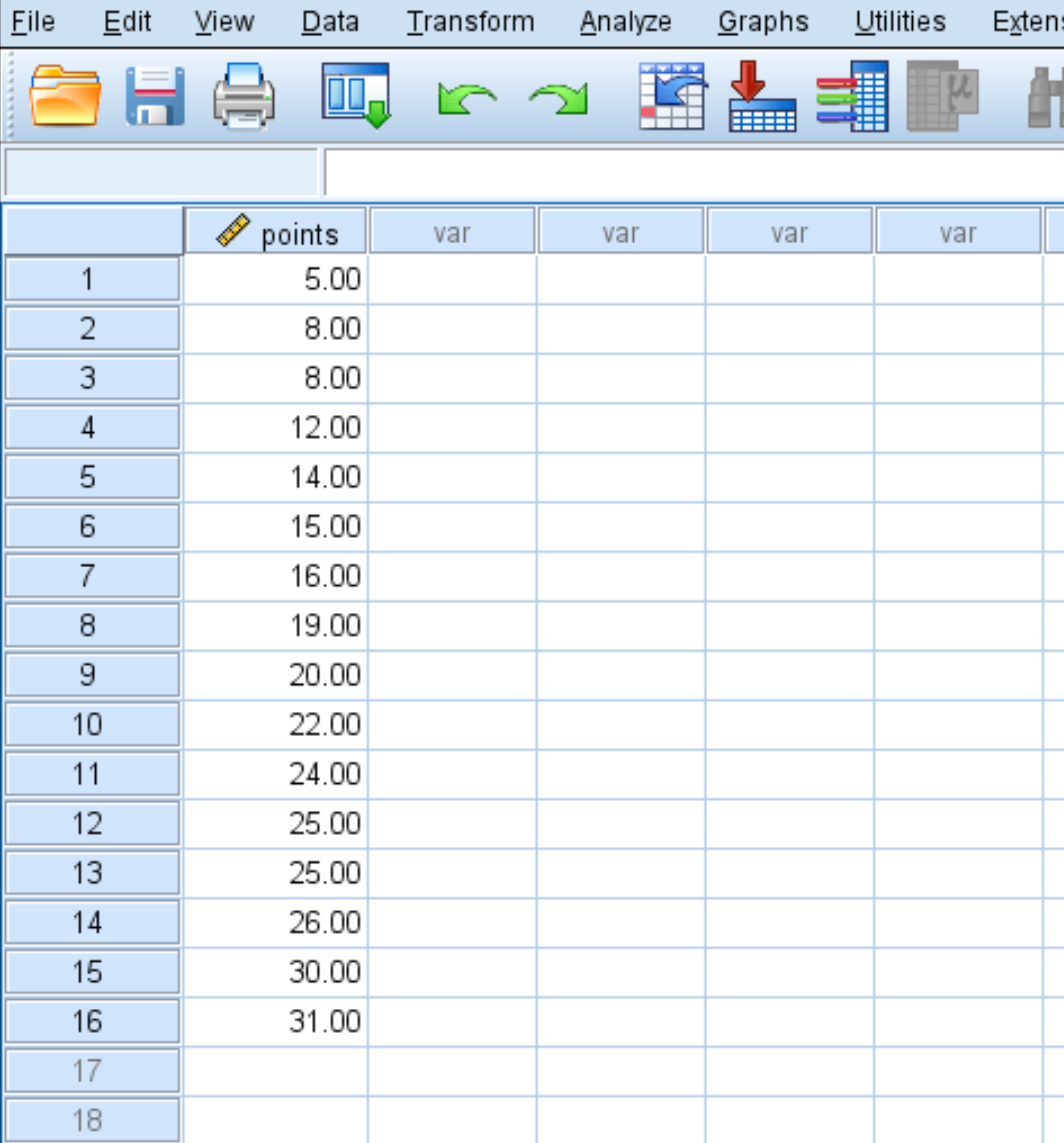
Pour créer une boîte à moustaches pour visualiser la distribution de ces valeurs de données, nous pouvons cliquer sur l’onglet Analyser , puis Statistiques descriptives , puis Explorer :

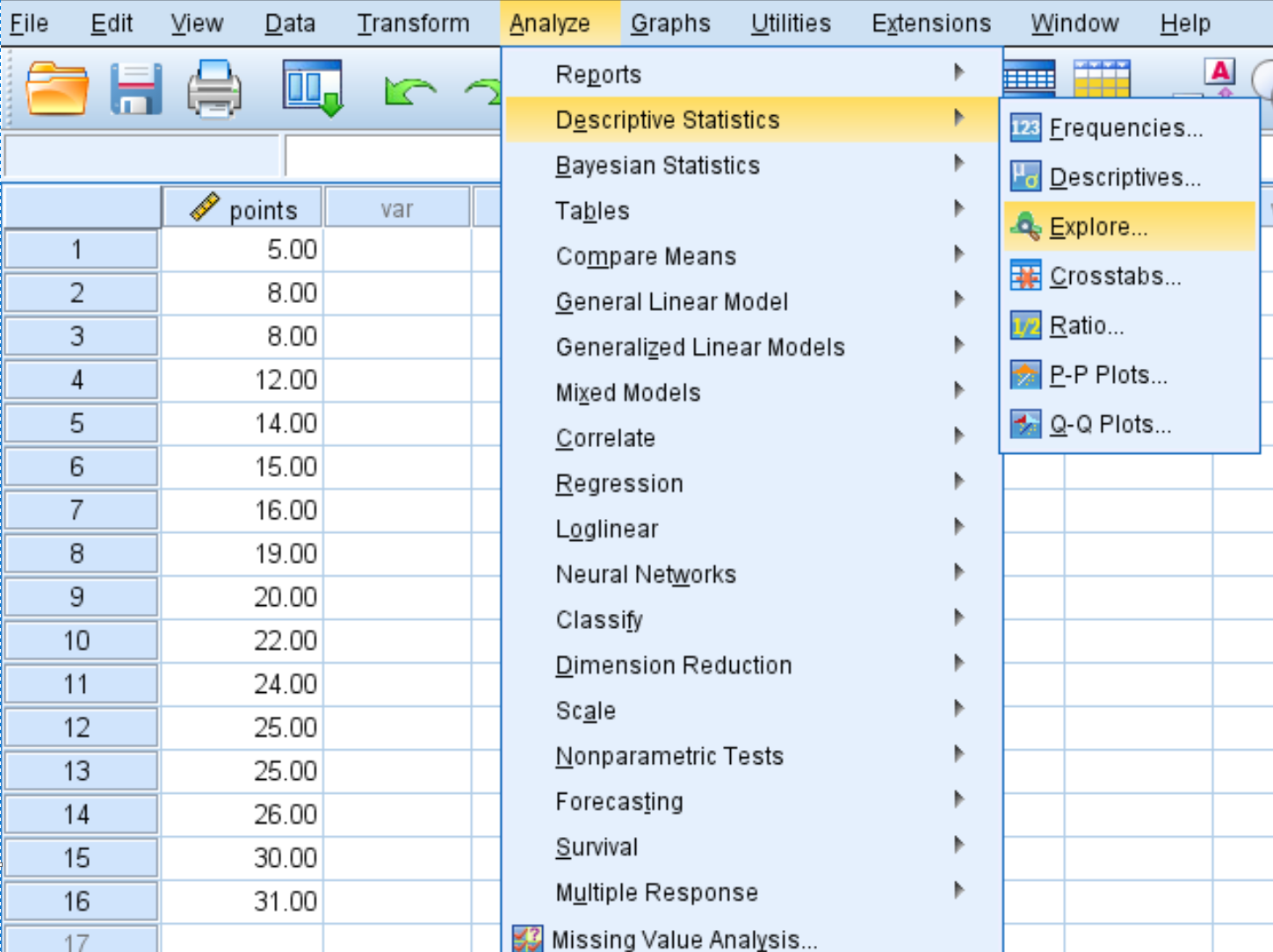
Cela fera apparaître la fenêtre suivante :

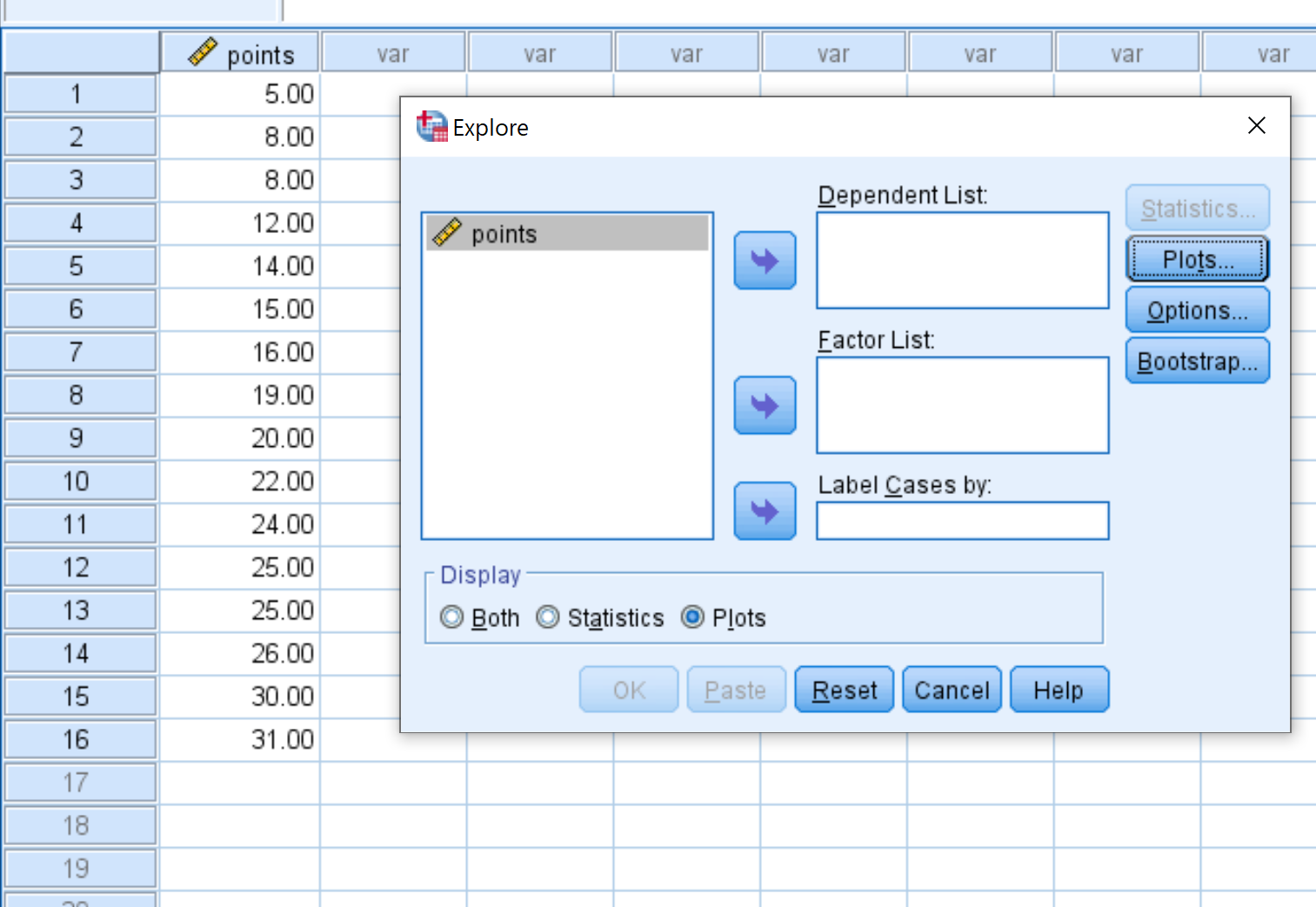
Pour créer une boîte à moustaches, faites glisser les points variables dans la zone intitulée Liste dépendante . Assurez-vous ensuite que Parcelles est sélectionnée sous l’option qui dit Afficher en bas de la boîte.

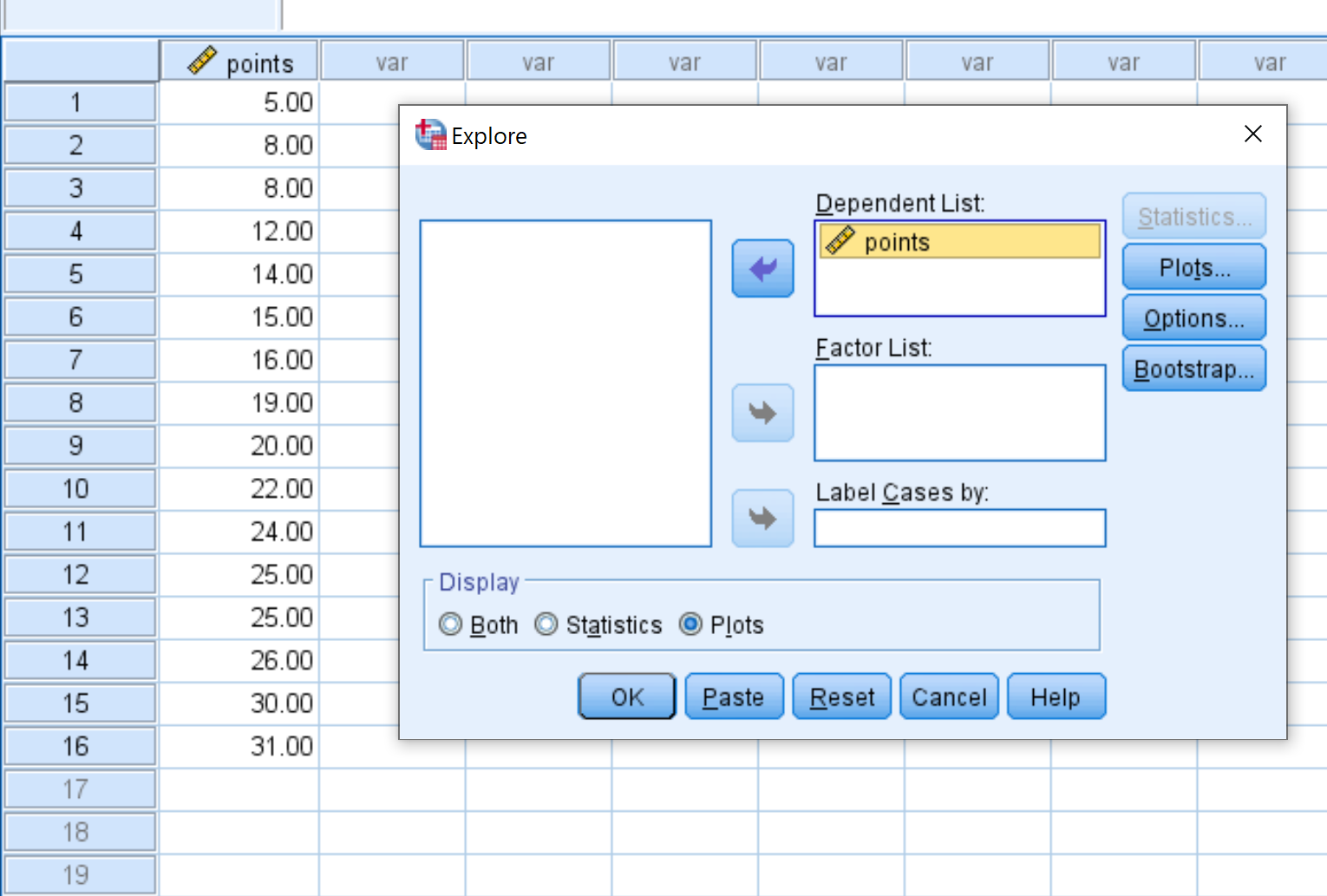
Une fois que vous avez cliqué sur OK , la boîte à moustaches suivante apparaît :

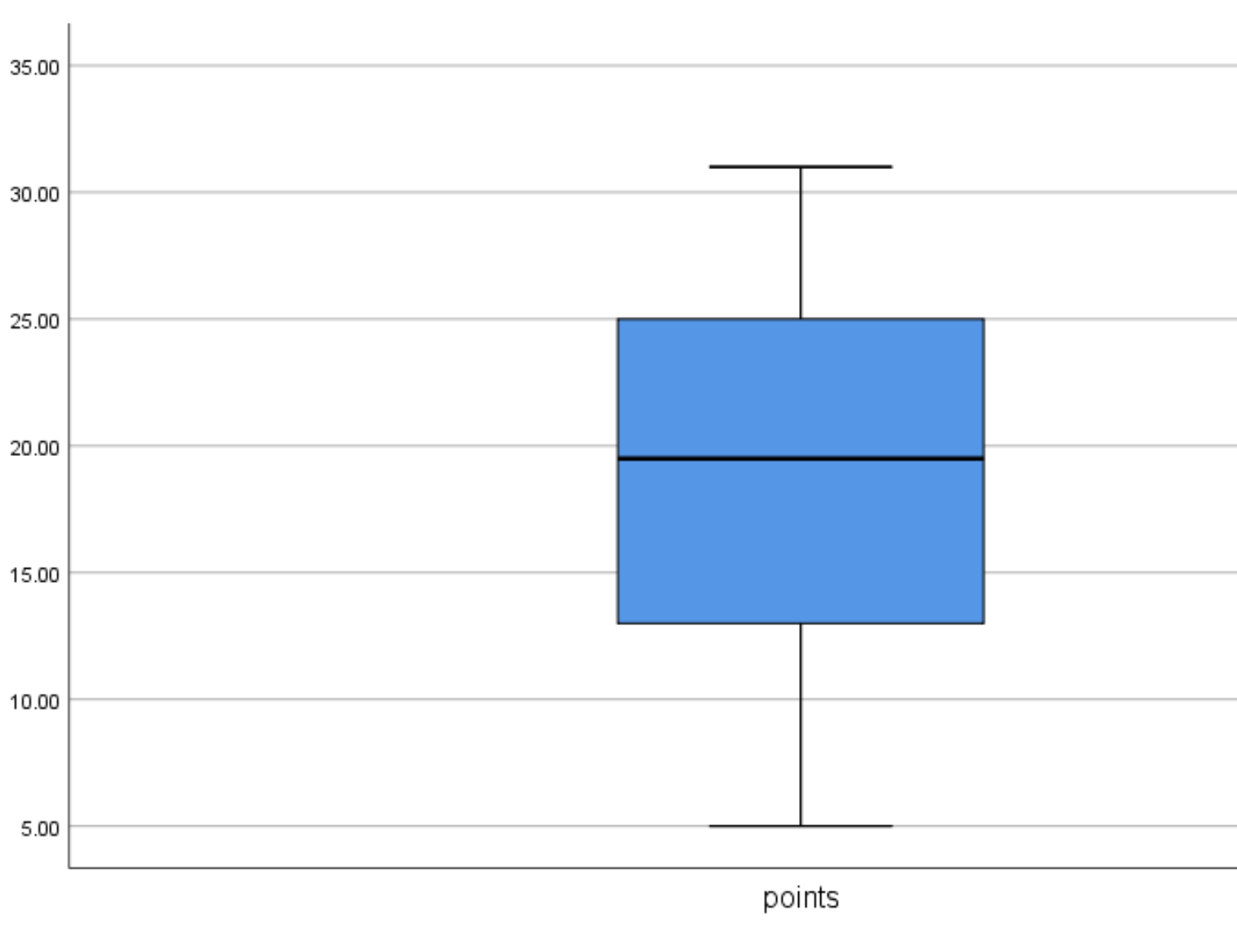
Voici comment interpréter cette boîte à moustaches :

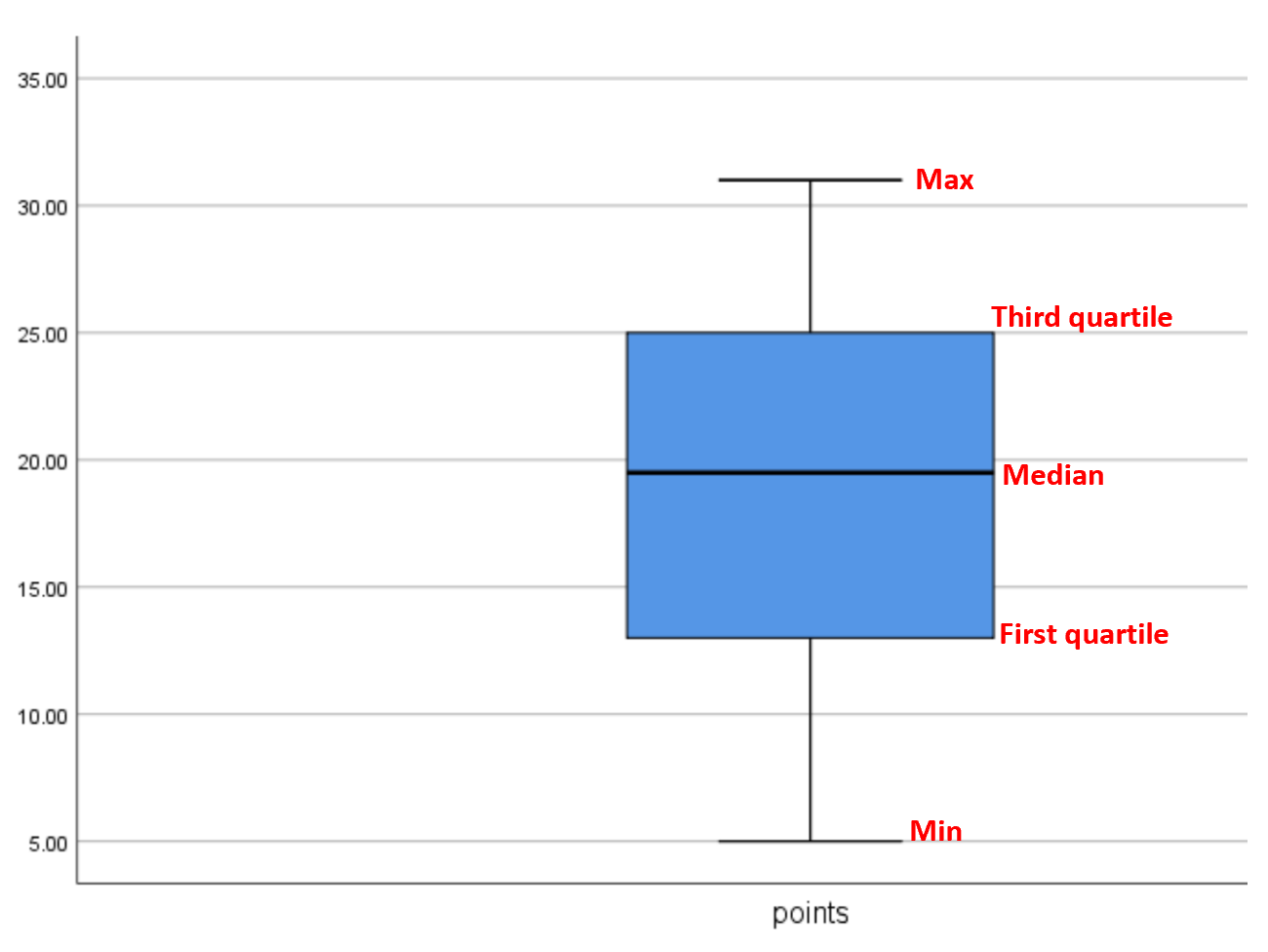
Une note sur les valeurs aberrantes

L’intervalle interquartile (IQR) est la distance entre le troisième quartile et le premier quartile. SPSS considère toute valeur de données comme une valeur aberrante si elle est 1,5 fois l’IQR supérieur au troisième quartile ou 1,5 fois l’IQR inférieur au premier quartile.

Les valeurs aberrantes sont affichées sous forme de petits cercles dans SPSS. Dans l’exemple précédent, il n’y avait pas de valeurs aberrantes, c’est pourquoi aucun petit cercle n’était affiché dans le diagramme en boîte. Cependant, si notre plus grande valeur dans l’ensemble de données était en réalité de 50, la boîte à moustaches afficherait un petit cercle pour indiquer la valeur aberrante :

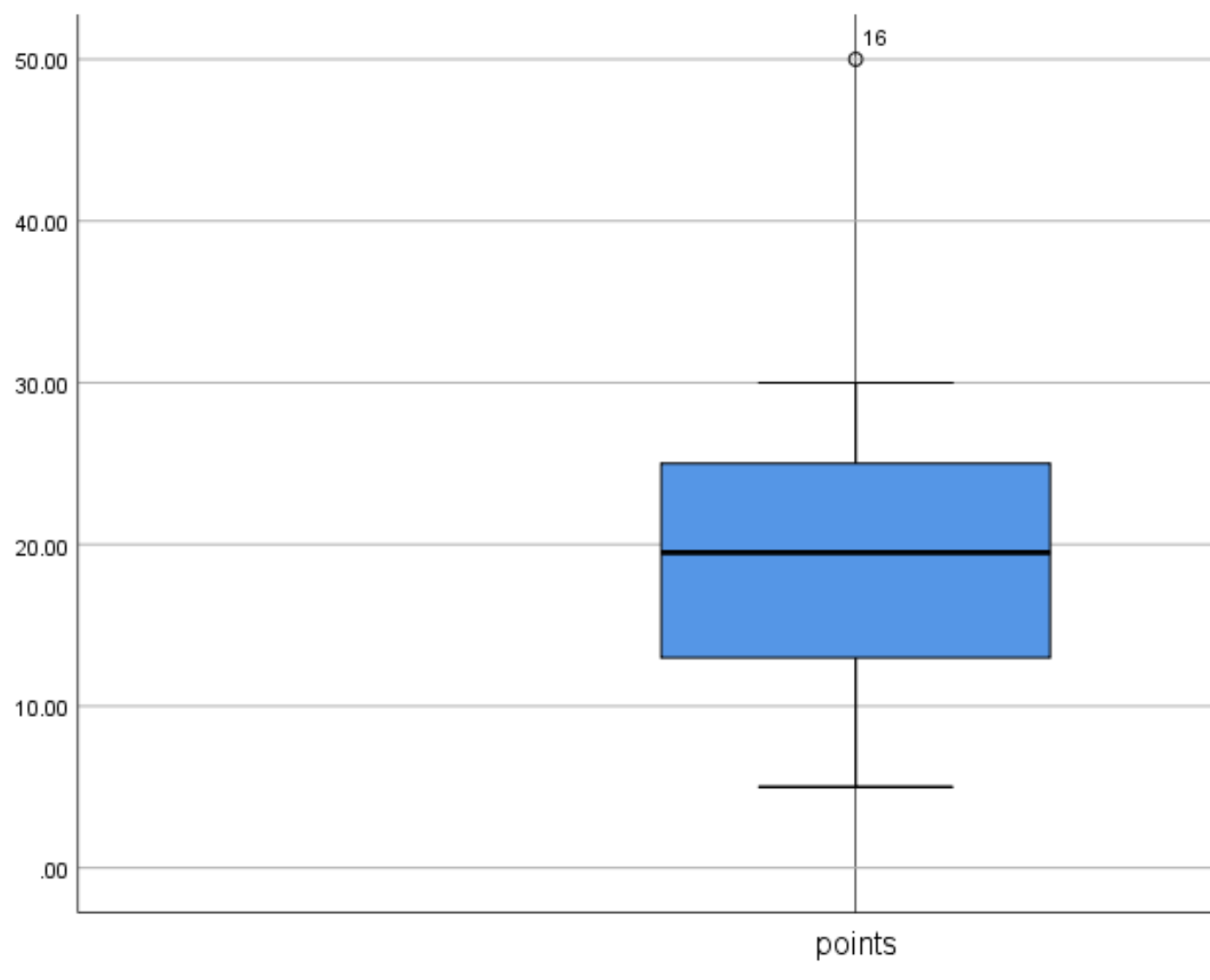
Si une valeur aberrante est présente dans votre ensemble de données, vous disposez de plusieurs options :

• Assurez-vous que la valeur aberrante n’est pas une erreur de saisie de données. Parfois, les valeurs des données sont simplement enregistrées de manière incorrecte. Si une valeur aberrante est présente, vérifiez d’abord que la valeur a été saisie correctement et qu’il ne s’agissait pas d’une erreur.
• Attribuez une nouvelle valeur à la valeur aberrante . Si la valeur aberrante s’avère être le résultat d’une erreur de saisie de données, vous pouvez décider de lui attribuer une nouvelle valeur telle que la moyenne ou la médiane de l’ensemble de données.
• Supprimez la valeur aberrante. Si la valeur est réellement aberrante, vous pouvez choisir de la supprimer si elle aura un impact significatif sur votre analyse globale. Assurez-vous simplement de mentionner dans votre rapport ou analyse final que vous avez supprimé une valeur aberrante.

Comment créer plusieurs boîtes à moustaches dans SPSS

Si vous disposez de plusieurs variables, SPSS peut également créer plusieurs boîtes à moustaches côte à côte. Par exemple, supposons que nous disposions des données suivantes sur la moyenne des points marqués par 16 joueurs de trois équipes différentes :

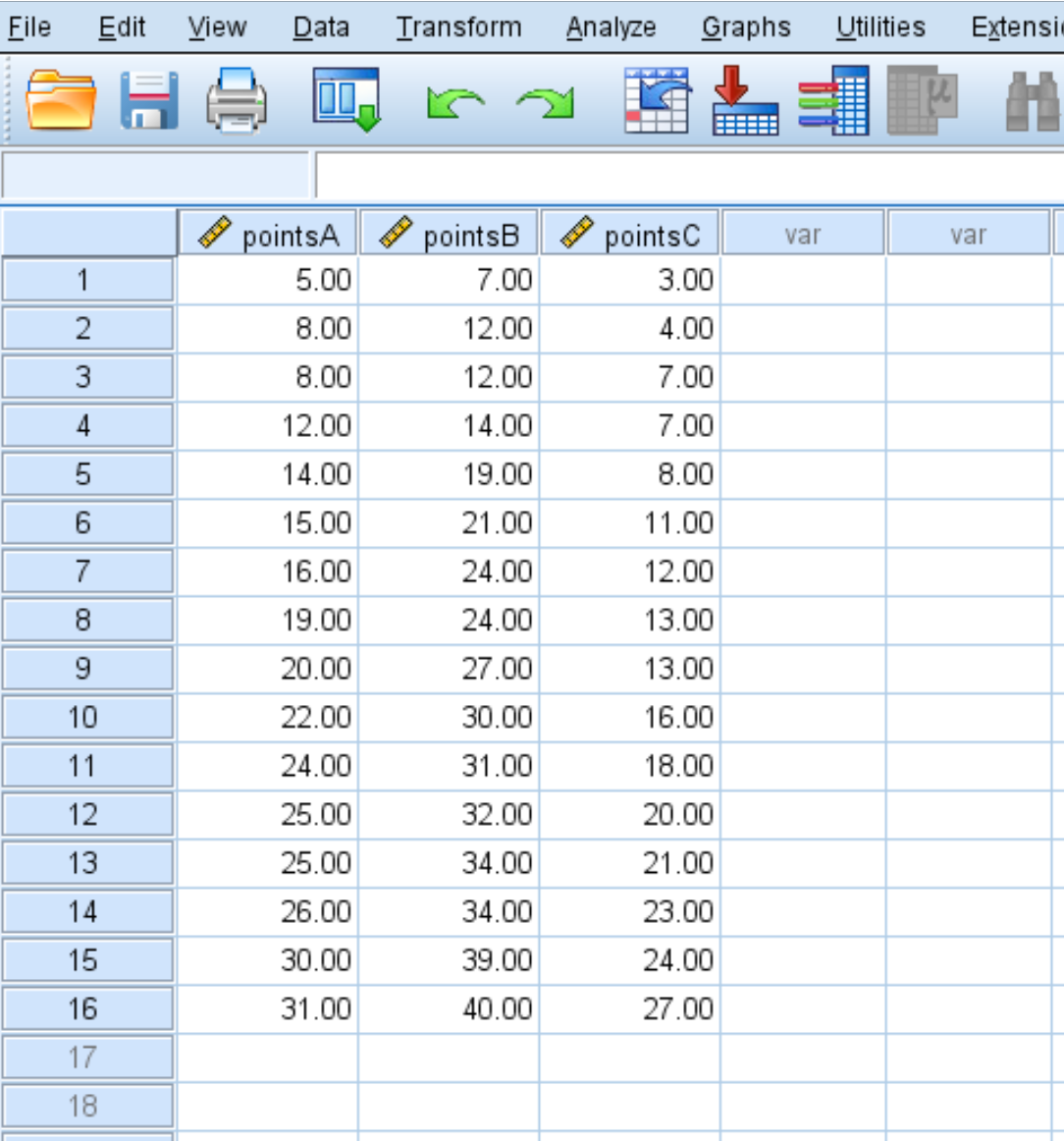
Pour créer une boîte à moustaches pour chacune de ces variables, on peut à nouveau cliquer sur l’onglet Analyser , puis Statistiques descriptives , puis Explorer . Nous pouvons ensuite faire glisser les trois variables dans la zone intitulée Dependent List :

Une fois que nous cliquons sur OK , les boîtes à moustaches suivantes apparaîtront :

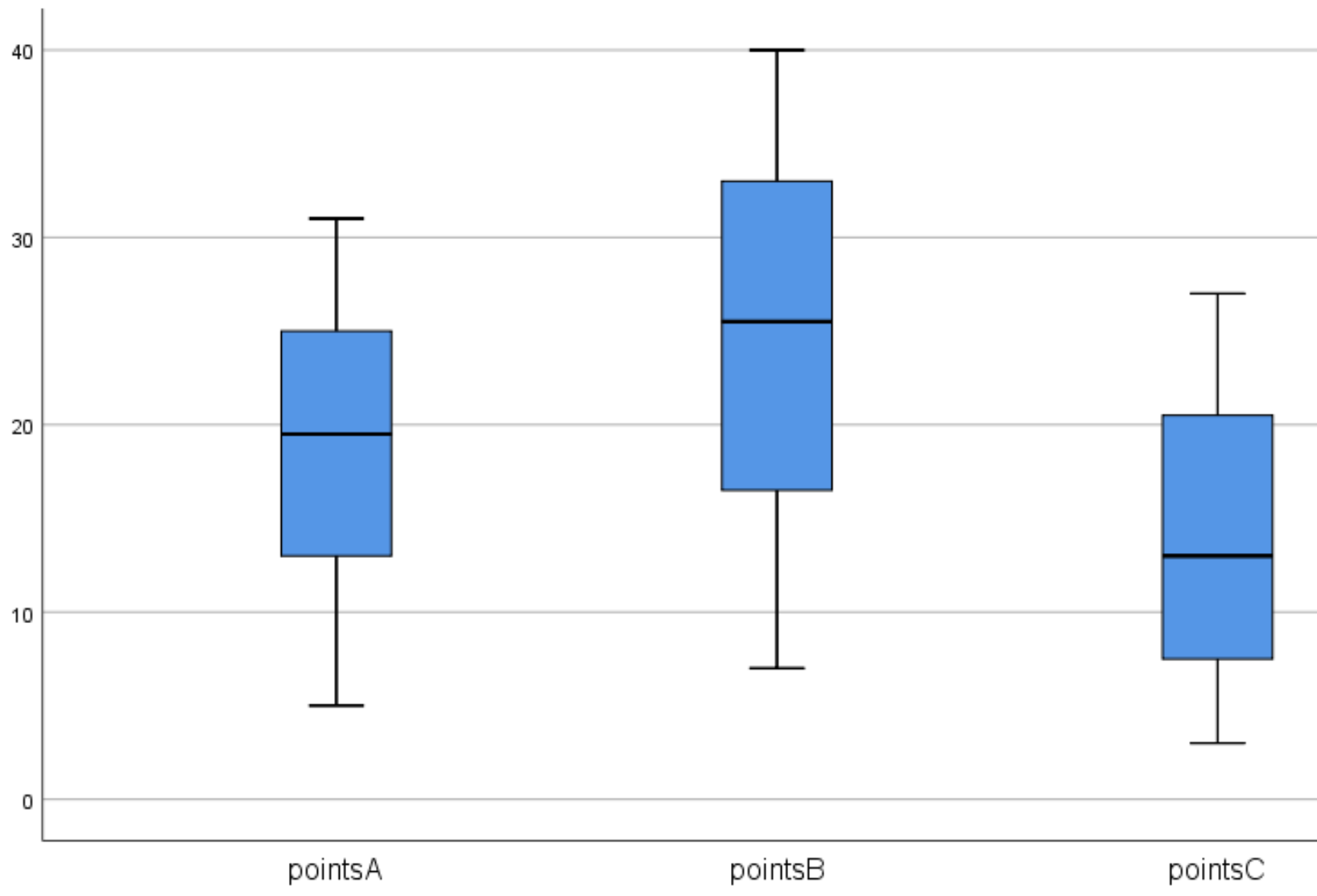
Cela nous aide à visualiser facilement les différences de répartitions entre ces trois équipes.

Nous pouvons également observer les éléments suivants :

• La médiane des points marqués par match est la plus élevée pour l’équipe B et la plus faible pour l’équipe C.
• La variation du nombre de points marqués par match est la plus élevée pour l’équipe B, comme en témoigne la durée de leur box plot par rapport à l’équipe A et à l’équipe C.
• Le joueur avec le plus de points par match fait partie de l’équipe B et celui avec le moins de points par match fait partie de l’équipe C.

Les boîtes à moustaches sont utiles car elles peuvent nous fournir de nombreuses informations sur la distribution des ensembles de données à partir d’un seul graphique.