Comment effectuer une régression quadratique dans R

Lorsque deux variables ont une relation linéaire, nous pouvons souvent utiliser une simple régression linéaire pour quantifier leur relation.

Cependant, lorsque deux variables ont une relation quadratique, nous pouvons utiliser la régression quadratique pour quantifier leur relation.

Ce tutoriel explique comment effectuer une régression quadratique dans R.

Exemple : régression quadratique dans R

Supposons que nous souhaitions comprendre la relation entre le nombre d’heures travaillées et le bonheur déclaré. Nous disposons des données suivantes sur le nombre d’heures travaillées par semaine et le niveau de bonheur déclaré (sur une échelle de 0 à 100) pour 11 personnes différentes :

Utilisez les étapes suivantes pour ajuster un modèle de régression quadratique dans R.

Étape 1 : Saisissez les données.

Tout d’abord, nous allons créer un bloc de données contenant nos données :

#create data
data <- data.frame(hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                   happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))

#view data 
data

   hours happiness
1      6        14
2      9        28
3     12        50
4     14        70
5     30        89
6     35        94
7     40        90
8     47        75
9     51        59
10    55        44
11    60        27

Étape 2 : Visualisez les données.

Ensuite, nous allons créer un nuage de points simple pour visualiser les données.

#create scatterplot
plot(data$hours, data$happiness, pch=16)

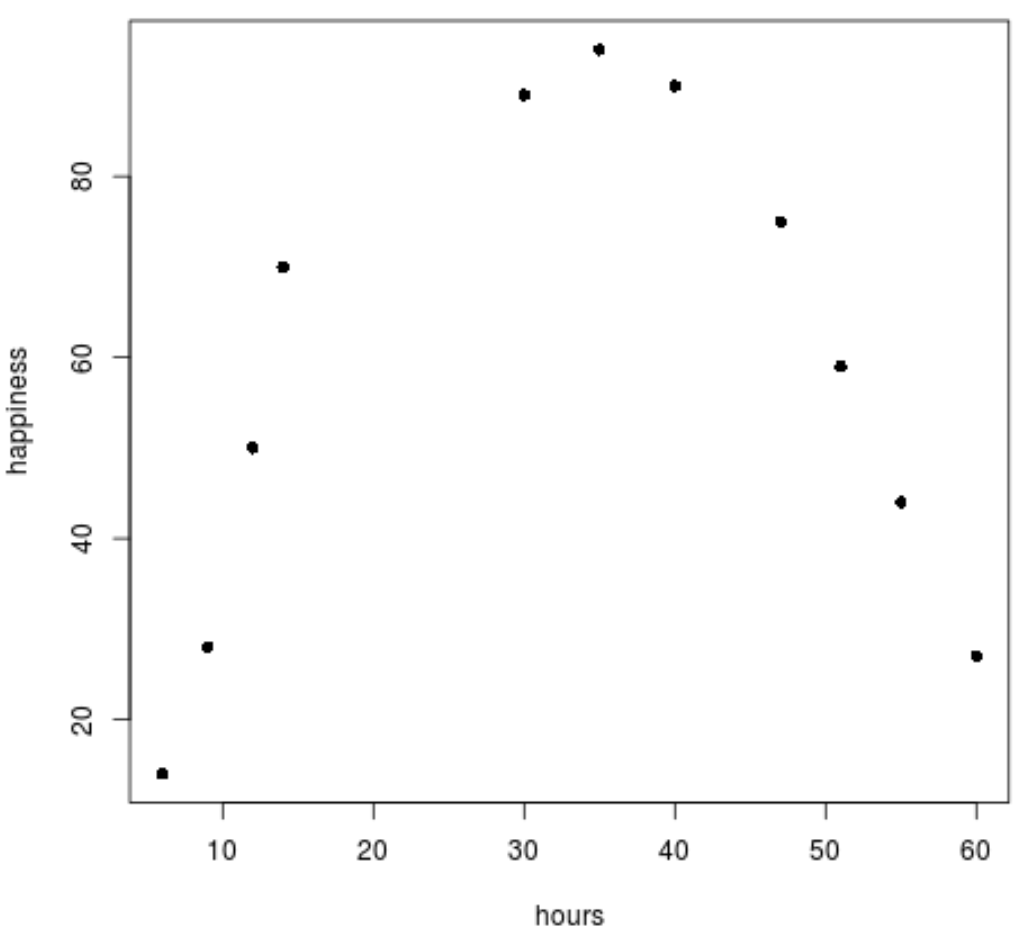
Nous pouvons clairement voir que les données ne suivent pas un modèle linéaire.

Étape 3 : Ajustez un modèle de régression linéaire simple.

Ensuite, nous ajusterons un modèle de régression linéaire simple pour voir dans quelle mesure il s’adapte aux données :

#fit linear model
linearModel <- lm(happiness ~ hours, data=data)

#view model summary
summary(linearModel)

Call:
lm(formula = happiness ~ hours)

Residuals:
   Min     1Q Median     3Q    Max 
-39.34 -21.99  -2.03  23.50  35.11 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)  48.4531    17.3288   2.796   0.0208 *
hours         0.2981     0.4599   0.648   0.5331  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 28.72 on 9 degrees of freedom
Multiple R-squared:  0.0446,	Adjusted R-squared:  -0.06156 
F-statistic: 0.4201 on 1 and 9 DF,  p-value: 0.5331

La variance totale du bonheur expliquée par le modèle n’est que de 4,46 % , comme le montre la valeur du R-carré multiple.

Étape 4 : Ajustez un modèle de régression quadratique.

Ensuite, nous ajusterons un modèle de régression quadratique.

#create a new variable for hours2
data$hours2 <- data$hours^2

#fit quadratic regression model
quadraticModel <- lm(happiness ~ hours + hours2, data=data)

#view model summary
summary(quadraticModel)

Call:
lm(formula = happiness ~ hours + hours2, data = data)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.2484 -3.7429 -0.1812  1.1464 13.6678 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364    6.18507  -2.951   0.0184 *  
hours         6.74436    0.48551  13.891 6.98e-07 ***
hours2       -0.10120    0.00746 -13.565 8.38e-07 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.218 on 8 degrees of freedom
Multiple R-squared:  0.9602,	Adjusted R-squared:  0.9502 
F-statistic: 96.49 on 2 and 8 DF,  p-value: 2.51e-06

La variance totale du bonheur expliquée par le modèle est passée à 96,02 % .

Nous pouvons utiliser le code suivant pour visualiser dans quelle mesure le modèle s’adapte aux données :

#create sequence of hour values
hourValues <- seq(0, 60, 0.1)

#create list of predicted happines levels using quadratic model
happinessPredict <- predict(quadraticModel,list(hours=hourValues, hours2=hourValues^2))

#create scatterplot of original data values
plot(data$hours, data$happiness, pch=16)
#add predicted lines based on quadratic regression model
lines(hourValues, happinessPredict, col='blue')

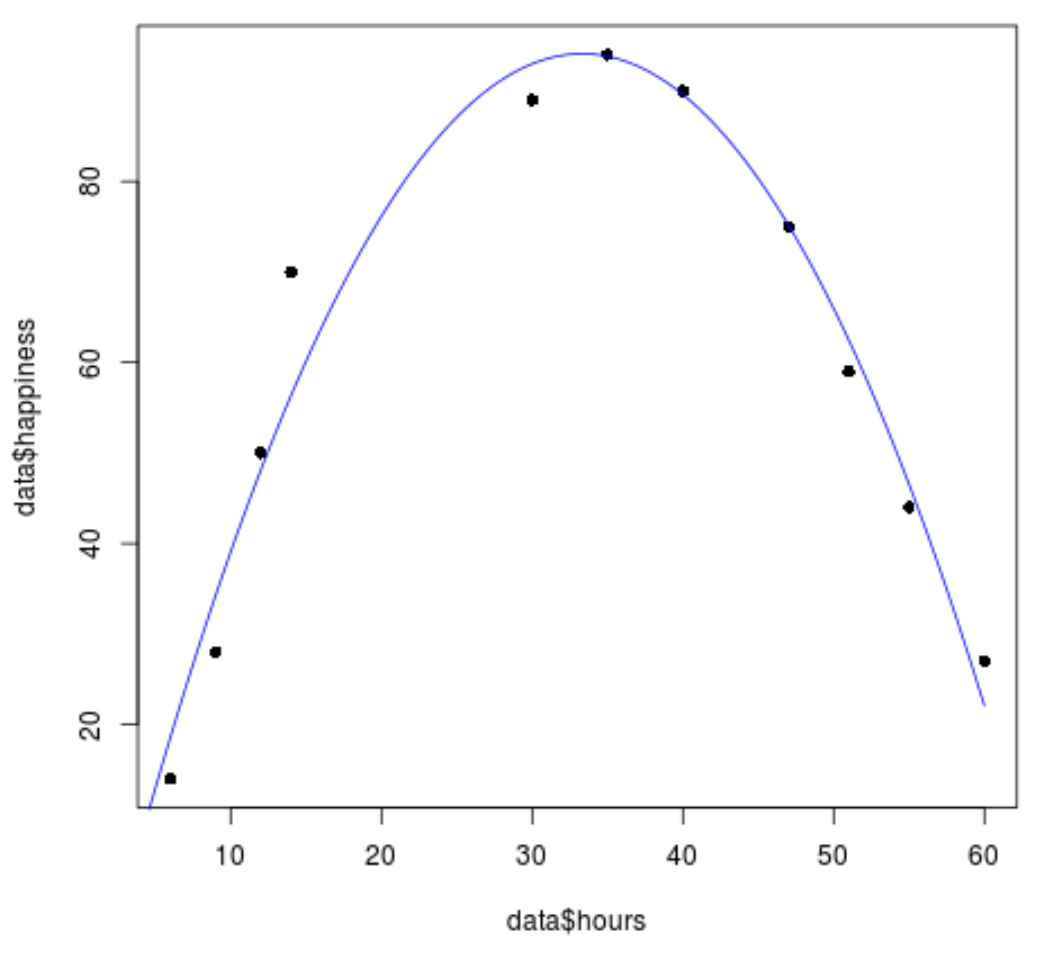
Nous pouvons voir que la droite de régression quadratique correspond assez bien aux valeurs des données.

Étape 5 : Interpréter le modèle de régression quadratique.

À l’étape précédente, nous avons vu que le résultat du modèle de régression quadratique était le suivant :

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364    6.18507  -2.951   0.0184 *  
hours         6.74436    0.48551  13.891 6.98e-07 ***
hours2       -0.10120    0.00746 -13.565 8.38e-07 ***

Sur la base des coefficients présentés ici, la régression quadratique ajustée serait :

Bonheur = -0,1012 (heures) ² + 6,7444 (heures) – 18,2536

Nous pouvons utiliser cette équation pour trouver le bonheur prédit d’un individu, compte tenu du nombre d’heures qu’il travaille par semaine.

Par exemple, une personne qui travaille 60 heures par semaine aurait un niveau de bonheur de 22,09 :

Bonheur = -0,1012(60) ² + 6,7444(60) – 18,2536 = 22,09

À l’inverse, une personne qui travaille 30 heures par semaine devrait avoir un niveau de bonheur de 92,99 :

Bonheur = -0,1012(30) ² + 6,7444(30) – 18,2536 = 92,99