Comment effectuer manuellement une ANOVA à mesures répétées
Une ANOVA à mesures répétées est utilisée pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes ou plus dans lesquels les mêmes sujets apparaissent dans chaque groupe.
Ce didacticiel explique comment effectuer manuellement une ANOVA à mesures répétées unidirectionnelles.
Exemple : ANOVA à mesures répétées unidirectionnelles à la main
Les chercheurs veulent savoir si trois médicaments différents entraînent des temps de réaction différents. Pour tester cela, ils mesurent le temps de réaction (en secondes) de cinq patients à chaque médicament. Les résultats sont montrés plus bas:
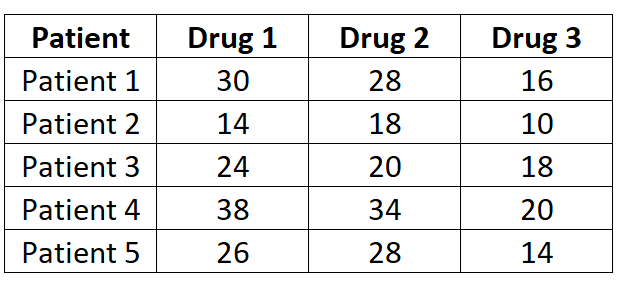
Étant donné que chaque patient est mesuré sur chacun des trois médicaments, nous utiliserons une ANOVA à mesures répétées unidirectionnelles pour déterminer si le temps de réaction moyen diffère entre les médicaments.
Suivez les étapes suivantes pour effectuer manuellement l’ANOVA à mesures répétées :
Étape 1 : Calculez la SST.
Tout d’abord, nous calculerons la somme totale des carrés (SST), qui peut être trouvée à l’aide de la formule suivante :
SST = s 2 total (n total -1)
où:
- s 2 total : la variance pour l’ensemble de données
- n total : le nombre total d’observations dans l’ensemble de données
Dans cet exemple, nous calculons le SST comme suit : (64,2667)(15-1) = 899,7
Étape 2 : Calculer la SSB
Ensuite, nous calculerons la somme des carrés (SSB), qui peut être trouvée à l’aide de la formule suivante :
SSB = Σn j ( x j – x total ) 2
où:
- Σ : un symbole grec qui signifie « somme »
- n j : le nombre total d’observations dans le j ème groupe
- x j : la moyenne du j ème groupe
- x total : la moyenne de l’ensemble des données
Dans cet exemple, nous calculons SSB comme suit : (5)(26,4-22,533) 2 +(5)(25,6-22,533) 2 + (5)(15,6-22,533) 2 = 362,1
Étape 3 : Calculez le SSS.
Ensuite, nous calculerons la somme des carrés du sujet (SSS), qui peut être trouvée à l’aide de la formule suivante :
SSS =(Σr 2 k /c) – (N 2 /rc)
où:
- Σ : un symbole grec qui signifie « somme »
- r 2 k : somme au carré du k ème patient
- N : le total général de l’ensemble des données
- r : nombre total de patients
- c : nombre total de groupes
Dans cet exemple, nous calculons SSS comme suit : ((74 2 + 42 2 + 62 2 + 92 2 + 68 2 )/3) – (338 2 /(5)(3)) = 441,1
Étape 4 : Calculez le SSE.
Ensuite, nous calculerons la somme des carrés d’erreur (SSE), qui peut être trouvée à l’aide de la formule suivante :
SSE = SST – SSB – SSS
Dans cet exemple, nous calculons le SSE comme suit : 899,7 – 362,1 – 441,1 = 96,5
Étape 5 : Remplissez le tableau ANOVA à mesures répétées.
Maintenant que nous avons SSB, SSS et SSE, nous pouvons remplir le tableau ANOVA à mesures répétées :
| Source | Somme des carrés (SS) | df | Carrés moyens (MS) | F |
|---|---|---|---|---|
| Entre | 362.1 | 2 | 181.1 | 15.006 |
| Sujet | 441.1 | 4 | 110.3 | |
| Erreur | 96,5 | 8 | 12.1 |
Voici comment nous avons calculé les différents nombres du tableau :
- df entre : #groupes – 1 = 3 – 1 = 2
- df sujet : #participants – 1 = 5 – 1 = 4
- Erreur df : df entre * df sujet = 2*4 = 8
- MS entre : SSB / df entre = 362,1 / 2 = 181,1
- Sujet MS : sujet SSS / df = 441,1 / 4 = 110,3
- Erreur MS : erreur SSE / df = 96,5 / 8 = 12,1
- F : MS entre / erreur MS = 181,1 / 12,1 = 15,006
Étape 6 : Interprétez les résultats.
La statistique du test F pour cette ANOVA à mesures répétées unidirectionnelles est de 15,006 . Pour déterminer s’il s’agit d’un résultat statistiquement significatif, nous devons le comparer à la valeur critique F trouvée dans letableau de distribution F avec les valeurs suivantes :
- α (niveau de signification) = 0,05
- DF1 (degrés de liberté du numérateur) = df entre = 2
- DF2 (degrés de liberté du dénominateur) = erreur df = 8
Nous trouvons que la valeur critique de F est de 4,459 .
Étant donné que la statistique du test F dans le tableau ANOVA est supérieure à la valeur critique F dans le tableau de distribution F, nous rejetons l’hypothèse nulle. Cela signifie que nous disposons de suffisamment de preuves pour affirmer qu’il existe une différence statistiquement significative entre les temps de réponse moyens des médicaments.
