Comment effectuer une ANOVA bidirectionnelle dans Excel

Une ANOVA bidirectionnelle (« analyse de variance ») est utilisée pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes indépendants ou plus qui ont été répartis sur deux facteurs.

Ce didacticiel explique comment effectuer une ANOVA bidirectionnelle dans Excel.

Exemple : ANOVA bidirectionnelle dans Excel

Un botaniste veut savoir si la croissance des plantes est influencée par l’exposition au soleil et la fréquence des arrosages. Elle plante 40 graines et les laisse pousser pendant deux mois dans différentes conditions d’exposition au soleil et de fréquence d’arrosage. Au bout de deux mois, elle enregistre la hauteur de chaque plante. Les résultats sont montrés plus bas:

Dans le tableau ci-dessus, nous voyons que cinq plantes ont été cultivées dans chaque combinaison de conditions. Par exemple, cinq plantes ont été cultivées avec un arrosage quotidien et sans lumière du soleil et leurs hauteurs après deux mois étaient de 4,8 pouces, 4,4 pouces, 3,2 pouces, 3,9 pouces et 4,4 pouces :

Nous pouvons utiliser les étapes suivantes pour effectuer une ANOVA bidirectionnelle sur ces données :

Étape 1 : Sélectionnez le Toolpak d’analyse de données.

Dans l’onglet Données , cliquez sur Analyse des données :

Si vous ne voyez pas cela comme une option, vous devez d’abord charger le Data Analysis Toolpak gratuit .

2. Choisissez Anova : deux facteurs avec réplication

Sélectionnez l’option qui dit Anova : Two-Factor With Replication , puis cliquez sur OK .

Dans ce contexte, la « réplication » fait référence au fait d’avoir plusieurs observations dans chaque groupe. Par exemple, plusieurs plantes étaient cultivées sans exposition au soleil et sans arrosage quotidien. Si, à la place, nous ne cultivions qu’une seule plante dans chaque combinaison de conditions, nous utiliserions « sans réplication », mais la taille de notre échantillon serait beaucoup plus petite.

3. Remplissez les valeurs nécessaires.

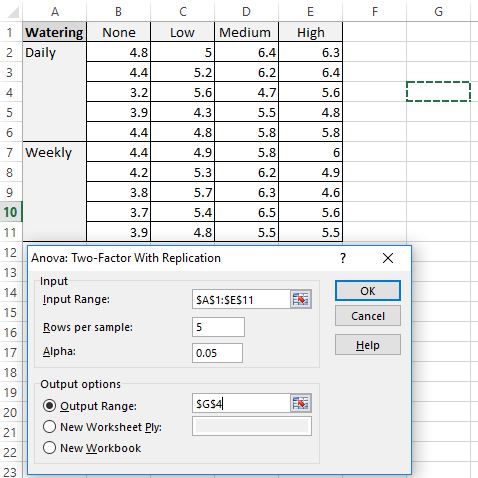
Ensuite, remplissez les valeurs suivantes :

• Plage d’entrée : sélectionnez la plage de cellules où se trouvent nos données, y compris les en-têtes.
• Lignes par échantillon : Tapez « 5 » car il y a 5 plantes dans chaque échantillon.
• Alpha : choisissez un niveau de signification à utiliser. Nous choisirons 0,05.
• Plage de sortie : choisissez une cellule dans laquelle vous souhaitez que la sortie de l’ANOVA bidirectionnelle apparaisse. Nous choisirons la cellule $G$4.

Étape 4 : Interprétez le résultat.

Une fois que nous cliquons sur OK , le résultat de l’ANOVA bidirectionnelle apparaîtra :

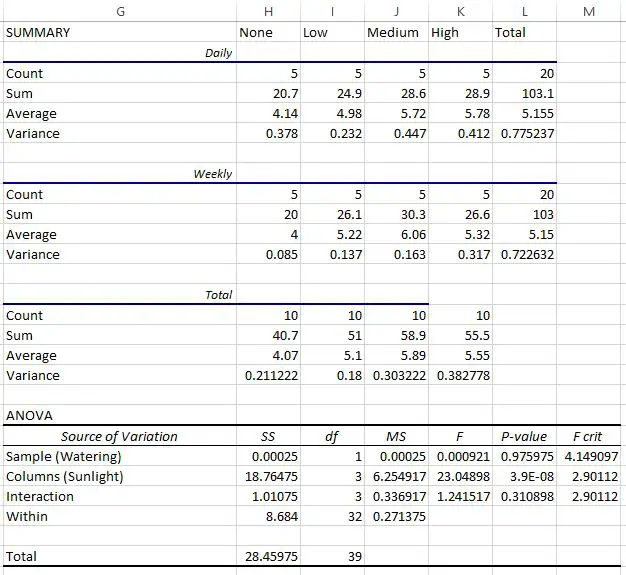
Les trois premiers tableaux présentent des statistiques récapitulatives pour chaque groupe. Par exemple:

• La hauteur moyenne des plantes arrosées quotidiennement mais sans lumière du soleil était de 4,14 pouces.
• La hauteur moyenne des plantes arrosées chaque semaine et bénéficiant d’un faible ensoleillement était de 5,22 pouces.
• La hauteur moyenne de toutes les plantes arrosées quotidiennement était de 5,115 pouces.
• La hauteur moyenne de toutes les plantes arrosées chaque semaine était de 5,15 pouces.
• La hauteur moyenne de toutes les plantes fortement exposées au soleil était de 5,55 pouces.

Et ainsi de suite.

Le dernier tableau montre le résultat de l’ANOVA bidirectionnelle. Nous pouvons observer les éléments suivants :

• La valeur p pour l’interaction entre la fréquence d’arrosage et l’exposition au soleil était de 0,310898 . Ceci n’est pas statistiquement significatif au niveau alpha de 0,05.
• La valeur p pour la fréquence d’arrosage était de 0,975975 . Ceci n’est pas statistiquement significatif au niveau alpha de 0,05.
• La valeur p pour l’exposition au soleil était de 3,9E-8 (0,000000039) . Ceci est statistiquement significatif au niveau alpha de 0,05.

Ces résultats indiquent que l’exposition au soleil est le seul facteur ayant un effet statistiquement significatif sur la hauteur des plantes. Et comme il n’y a pas d’effet d’interaction, l’effet de l’exposition au soleil est cohérent à chaque niveau de fréquence d’arrosage. Autrement dit, le fait qu’une plante soit arrosée quotidiennement ou hebdomadairement n’a aucun impact sur la façon dont l’exposition au soleil affecte une plante.