Une introduction à la distribution géométrique

La distribution géométrique décrit la probabilité de connaître un certain nombre d’échecs avant de connaître le premier succès d’une série d’essais de Bernoulli.

Un essai de Bernoulli est une expérience avec seulement deux résultats possibles – « succès » ou « échec » – et la probabilité de succès est la même à chaque fois que l’expérience est menée.

Un exemple d’essai de Bernoulli est un tirage au sort. La pièce ne peut atterrir que sur deux faces (on pourrait appeler face un « succès » et face un « échec ») et la probabilité de succès à chaque lancer est de 0,5, en supposant que la pièce soit juste.

Si une variable aléatoire X suit une distribution géométrique, alors la probabilité de connaître k échecs avant de connaître le premier succès peut être trouvée par la formule suivante :

P(X=k) = (1-p) ^kp

où:

• k : nombre d’échecs avant le premier succès
• p : probabilité de succès à chaque essai

Par exemple, supposons que nous voulions savoir combien de fois nous devrons lancer une pièce juste jusqu’à ce qu’elle tombe sur face. Nous pouvons utiliser la formule ci-dessus pour déterminer la probabilité de connaître 0, 1, 2, 3 échecs, etc. avant que la pièce n’atterrisse sur face :

Remarque : la pièce peut connaître 0 « échec » si elle tombe sur face au premier lancer.

P(X=0) = (1-.5) ⁰ (.5) = 0.5

P(X=1) = (1-.5) ¹ (.5) = 0.25

P(X=2) = (1-.5) ² (.5) = 0.125

P(X=3) = (1-0,5) ³ (0,5) = 0,0625

Nous pouvons calculer la probabilité d’un nombre quelconque de lancers de pièces jusqu’à l’infini. Nous créons ensuite un histogramme simple pour visualiser cette distribution de probabilité :

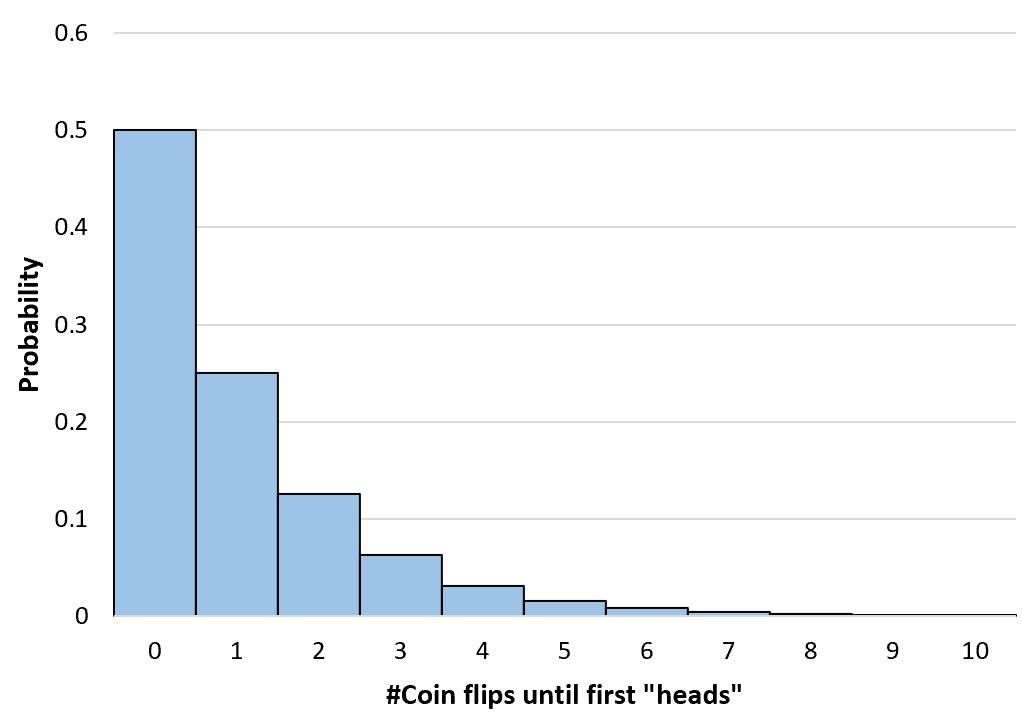
Calcul des probabilités géométriques cumulées

La probabilité cumulée que nous subissions k échecs ou moins jusqu’au premier succès peut être trouvée par la formule suivante :

P(X≤k) = 1 – (1-p) ^k+1

où:

• k : nombre d’échecs avant le premier succès
• p : probabilité de succès à chaque essai

Par exemple, supposons que nous souhaitions connaître la probabilité qu’il faille trois « échecs » ou moins avant que la pièce n’atterrisse finalement sur face. Nous utiliserions la formule suivante pour calculer cette probabilité :

P(X≤3) = 1 – (1-0,5) ³⁺¹ = 0,9375

Nous pouvons calculer chaque probabilité cumulée en utilisant une formule similaire :

P(X≤0) = 1 – (1-.5) ⁰⁺¹ = 0.5

P(X≤1) = 1 – (1-0,5) ¹⁺¹ = 0,75

P(X≤2) = 1 – (1-0,5) ²⁺¹ = 0,875

Nous pouvons calculer ces probabilités cumulées pour n’importe quel nombre de lancers de pièces jusqu’à l’infini. Nous pouvons ensuite créer un histogramme pour visualiser cette distribution de probabilité cumulée :

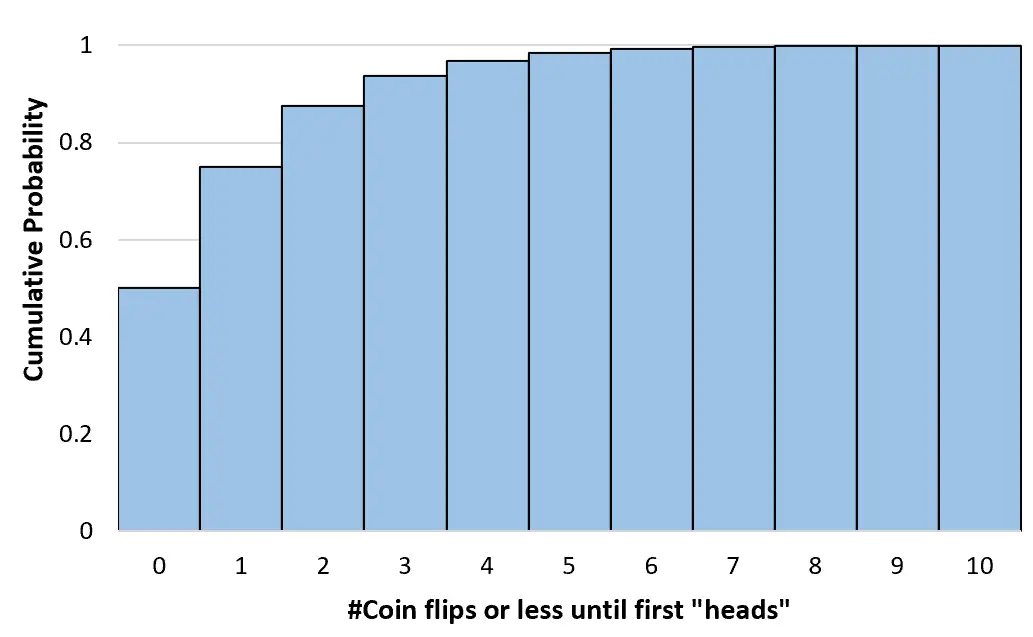
Propriétés de la distribution géométrique

La distribution géométrique a les propriétés suivantes :

La moyenne de la distribution est (1-p) / p .

La variance de la distribution est (1-p) / p ² .

Par exemple:

Le nombre moyen de fois où nous nous attendons à ce qu’une pièce atterrisse sur pile avant d’atterrir sur face serait (1-p) / p = (1-.5) / .5 = 1 .

La variance du nombre de lancers jusqu’à ce qu’il atterrisse sur face serait (1-p) / p ² = (1-.5) / .5 ² = 2 .

Problèmes de pratique de distribution géométrique

Utilisez les problèmes pratiques suivants pour tester vos connaissances de la distribution géométrique.

Remarque : Nous utiliserons le calculateur de distribution géométrique pour calculer les réponses à ces questions.

Problème 1

Question : Un chercheur attend à l’extérieur d’une bibliothèque pour demander aux gens s’ils soutiennent une certaine loi. La probabilité qu’une personne donnée soutienne la loi est p = 0,2. Quelle est la probabilité que la quatrième personne à qui le chercheur s’adresse soit la première à soutenir la loi ?

Réponse : Le nombre d’« échecs » jusqu’au premier succès – c’est-à-dire le nombre de personnes qui ne soutiennent pas la loi jusqu’à ce que la première personne la soutienne – est de 3. Ainsi, en utilisant le calculateur de distribution géométrique avec p = 0,2 et x = 3 échecs, on trouve que P(X=3) = 0.10240 .

Problème 2

Question : Un chercheur attend à l’extérieur d’une bibliothèque pour demander aux gens s’ils soutiennent une certaine loi. La probabilité qu’une personne donnée soutienne la loi est p = 0,2. Quelle est la probabilité que le chercheur doive parler à plus de quatre personnes pour trouver quelqu’un qui soutient la loi ?

Réponse : En utilisant le calculateur de distribution géométrique avec p =0,2 et x = 4 échecs, nous trouvons que P(X>4) = 0,32768 .

Problème 3

Question : Un chercheur attend à l’extérieur d’une bibliothèque pour demander aux gens s’ils soutiennent une certaine loi. La probabilité qu’une personne donnée soutienne la loi est p = 0,2. Quel est le nombre prévu de personnes à qui la chercheuse devra parler jusqu’à ce qu’elle trouve quelqu’un qui soutient la loi ?

Réponse : Rappelons que la moyenne de la distribution géométrique est (1-p) / p . Dans cette situation, la moyenne serait (1-.2) / .2 = 4 .