Test t à deux échantillons : définition, formule et exemple
Un test t à deux échantillons est utilisé pour déterminer si les moyennes de deux populations sont égales ou non.
Ce tutoriel explique les éléments suivants :
- La motivation pour effectuer un test t à deux échantillons.
- La formule pour effectuer un test t à deux échantillons.
- Les hypothèses qui doivent être respectées pour effectuer un test t à deux échantillons.
- Un exemple de la façon d’effectuer un test t à deux échantillons.
Test t à deux échantillons : Motivation
Supposons que nous voulions savoir si le poids moyen de deux espèces différentes de tortues est égal ou non. Comme il y a des milliers de tortues dans chaque population, il serait trop long et coûteux de faire le tour et de peser chaque tortue individuellement.
Au lieu de cela, nous pourrions prendre un échantillon aléatoire simple de 15 tortues de chaque population et utiliser le poids moyen de chaque échantillon pour déterminer si le poids moyen est égal entre les deux populations :
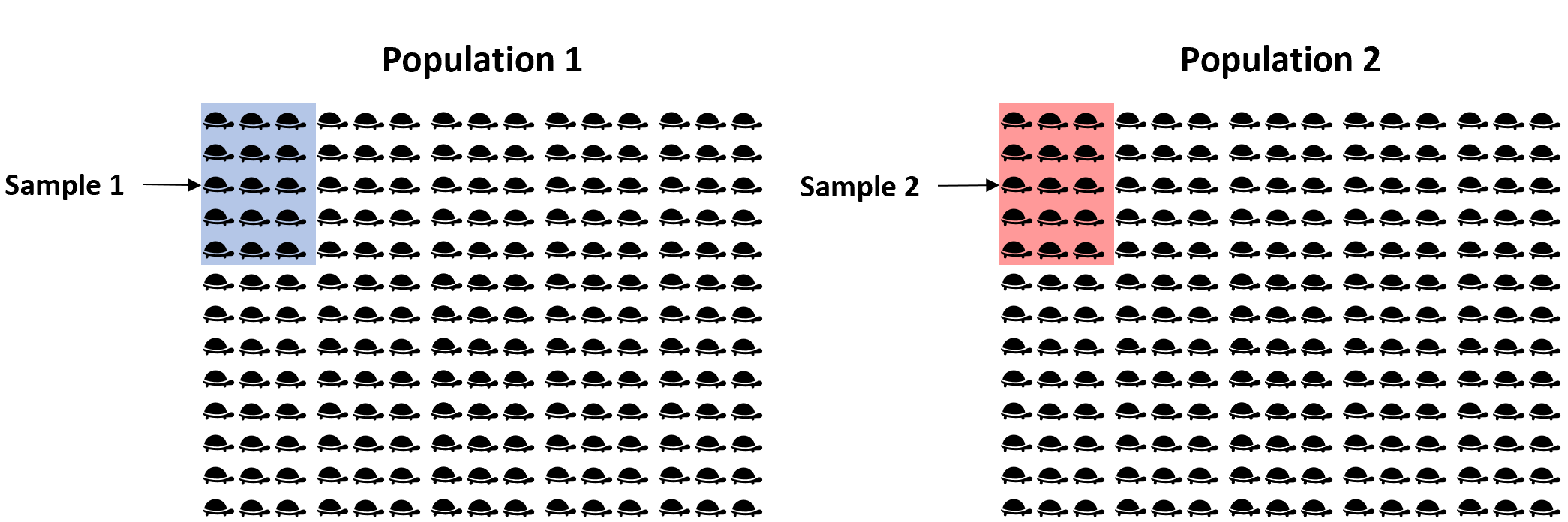
Cependant, il est pratiquement garanti que le poids moyen entre les deux échantillons sera au moins un peu différent. La question est de savoir si cette différence est statistiquement significative . Heureusement, un test t à deux échantillons nous permet de répondre à cette question.
Test t à deux échantillons : formule
Un test t à deux échantillons utilise toujours l’hypothèse nulle suivante :
- H 0 : μ 1 = μ 2 (les deux moyennes de population sont égales)
L’hypothèse alternative peut être bilatérale, à gauche ou à droite :
- H 1 (bilatéral) : μ 1 ≠ μ 2 (les moyennes des deux populations ne sont pas égales)
- H 1 (à gauche) : μ 1 < μ 2 (la moyenne de la population 1 est inférieure à la moyenne de la population 2)
- H 1 (à droite) : μ 1 > μ 2 (la moyenne de la population 1 est supérieure à la moyenne de la population 2)
Nous utilisons la formule suivante pour calculer la statistique de test t :
Statistique de test : ( x 1 – x 2 ) / s p (√ 1/n 1 + 1/n 2 )
où x 1 et x 2 sont les moyennes de l’échantillon, n 1 et n 2 sont les tailles d’échantillon, et où s p est calculé comme suit :
s p = √ (n 1 -1)s 1 2 + (n 2 -1)s 2 2 / (n 1 +n 2 -2)
où s 1 2 et s 2 2 sont les variances de l’échantillon.
Si la valeur p qui correspond à la statistique de test t avec (n 1 + n 2 -1) degrés de liberté est inférieure au niveau de signification que vous avez choisi (les choix courants sont 0,10, 0,05 et 0,01), alors vous pouvez rejeter l’hypothèse nulle. .
Test t à deux échantillons : hypothèses
Pour que les résultats d’un test t sur deux échantillons soient valides, les hypothèses suivantes doivent être respectées :
- Les observations d’un échantillon doivent être indépendantes des observations de l’autre échantillon.
- Les données doivent être distribuées à peu près normalement.
- Les deux échantillons devraient avoir à peu près la même variance. Si cette hypothèse n’est pas remplie, vous devez plutôt effectuer le test t de Welch .
- Les données des deux échantillons ont été obtenues à l’aide d’une méthode d’échantillonnage aléatoire .
Test t à deux échantillons : exemple
Supposons que nous voulions savoir si le poids moyen de deux espèces différentes de tortues est égal ou non. Pour tester cela, nous effectuerons un test t à deux échantillons au niveau de signification α = 0,05 en suivant les étapes suivantes :
Étape 1 : Rassemblez les exemples de données.
Supposons que nous collections un échantillon aléatoire de tortues de chaque population avec les informations suivantes :
Échantillon 1 :
- Taille de l’échantillon n 1 = 40
- Poids moyen de l’échantillon x 1 = 300
- Écart type de l’échantillon s 1 = 18,5
Échantillon 2 :
- Taille de l’échantillon n 2 = 38
- Poids moyen de l’échantillon x 2 = 305
- Écart type de l’échantillon s 2 = 16,7
Étape 2 : Définir les hypothèses.
Nous effectuerons le test t à deux échantillons avec les hypothèses suivantes :
- H 0 : μ 1 = μ 2 (les deux moyennes de population sont égales)
- H 1 : μ 1 ≠ μ 2 (les deux moyennes de population ne sont pas égales)
Étape 3 : Calculez la statistique de test t .
Tout d’abord, nous calculerons l’ écart type poolé s p :
s p = √ (n 1 -1)s 1 2 + (n 2 -1)s 2 2 / (n 1 +n 2 -2) = √ (40-1)18,5 2 + (38-1)16,7 2 / (40+38-2) = 17,647
Ensuite, nous calculerons la statistique de test t :
t = ( x 1 – x 2 ) / s p (√ 1/n 1 + 1/n 2 ) = (300-305) / 17,647(√ 1/40 + 1/38 ) = -1,2508
Étape 4 : Calculez la valeur p de la statistique de test t .
Selon le calculateur T Score to P Value Calculator , la valeur p associée à t = -1,2508 et aux degrés de liberté = n 1 + n 2 -2 = 40+38-2 = 76 est 0,21484 .
Étape 5 : Tirez une conclusion.
Puisque cette valeur p n’est pas inférieure à notre niveau de signification α = 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle. Nous ne disposons pas de preuves suffisantes pour affirmer que le poids moyen des tortues entre ces deux populations est différent.
Remarque : Vous pouvez également effectuer l’intégralité de ce test t à deux échantillons en utilisant simplement le calculateur de test t à deux échantillons .
Ressources additionnelles
Les didacticiels suivants expliquent comment effectuer un test t sur deux échantillons à l’aide de différents programmes statistiques :
Comment effectuer un test t à deux échantillons dans Excel
Comment effectuer un test t à deux échantillons dans SPSS
Comment effectuer un test t à deux échantillons dans Stata
Comment effectuer un test t à deux échantillons dans R
Comment effectuer un test t à deux échantillons en Python
Comment effectuer un test t à deux échantillons sur une calculatrice TI-84
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus