Comment appliquer le théorème de Chebyshev dans Excel

Le théorème de Chebyshev stipule que pour tout nombre k supérieur à 1, au moins 1 – 1/k ² des valeurs de données dans toute distribution formée se situent dans k écarts types de la moyenne.

Par exemple, pour toute distribution façonnée, au moins 1 – 1/3 ² = 88,89 % des valeurs de la distribution se situeront à moins de 3 écarts types de la moyenne.

Ce didacticiel illustre plusieurs exemples d’application du théorème de Chebyshev dans Excel.

Exemple 1 : utilisez le théorème de Chebyshev pour déterminer quel pourcentage de valeurs se situera entre 30 et 70 pour un ensemble de données avec une moyenne de 50 et un écart type de 10.

Tout d’abord, déterminez la valeur de k. Nous pouvons le faire en déterminant combien d’écarts types se trouvent entre 30 et 70 par rapport à la moyenne :

(30 – moyenne) / écart type = (30 – 50) / 10 = -20 / 10 = -2

(70 – moyenne) / écart type = (70 – 50) / 10 = 20 / 10 = 2

Les valeurs 30 et 70 sont respectivement 2 écarts types en dessous et au-dessus de la moyenne. Ainsi, k = 2 .

Nous pouvons ensuite utiliser la formule suivante dans Excel pour trouver le pourcentage minimum de valeurs qui se situent dans 2 écarts types de la moyenne pour cet ensemble de données :

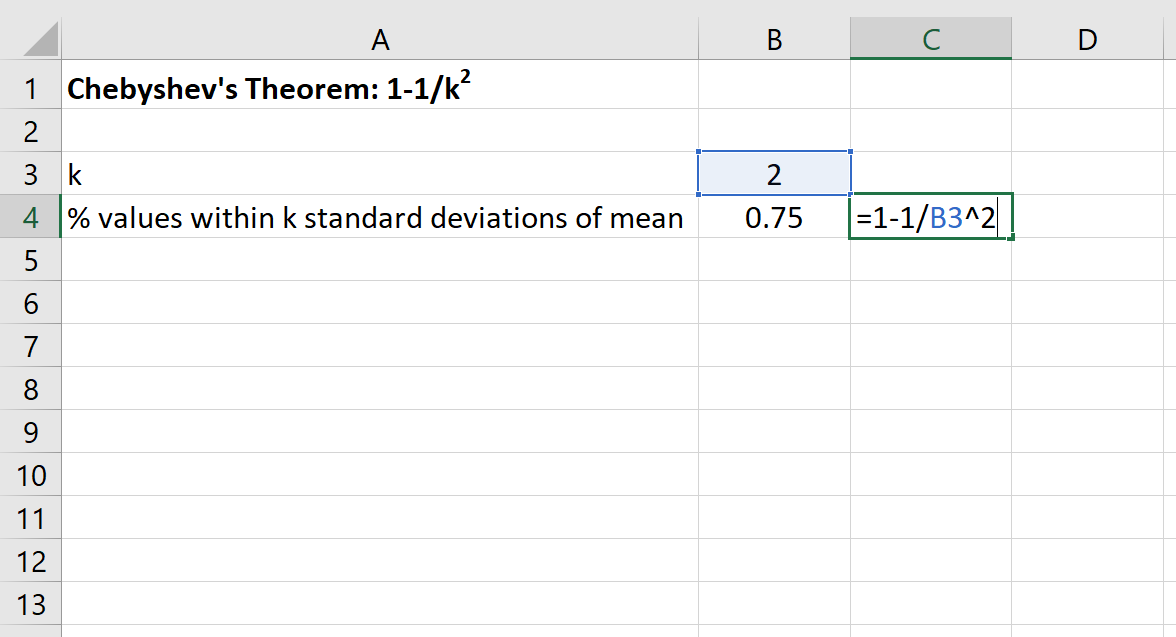
Le pourcentage de valeurs comprises entre 30 et 70 pour cet ensemble de données sera d’au moins 75 % .

Exemple 2 : utilisez le théorème de Chebyshev pour déterminer quel pourcentage de valeurs se situera entre 20 et 50 pour un ensemble de données avec une moyenne de 35 et un écart type de 5.

Tout d’abord, déterminez la valeur de k. Nous pouvons le faire en déterminant combien d’écarts types se trouvent entre 20 et 50 par rapport à la moyenne :

(20 – moyenne) / écart type = (20 – 35) / 5 = -15 / 5 = -3

(50 – moyenne) / écart type = (50 – 35) / 5 = 15 / 5 = 3

Les valeurs 20 et 50 sont respectivement 3 écarts types en dessous et au-dessus de la moyenne. Ainsi, k = 3 .

Nous pouvons ensuite utiliser la formule suivante dans Excel pour trouver le pourcentage minimum de valeurs qui se situent dans 3 écarts types de la moyenne pour cet ensemble de données :

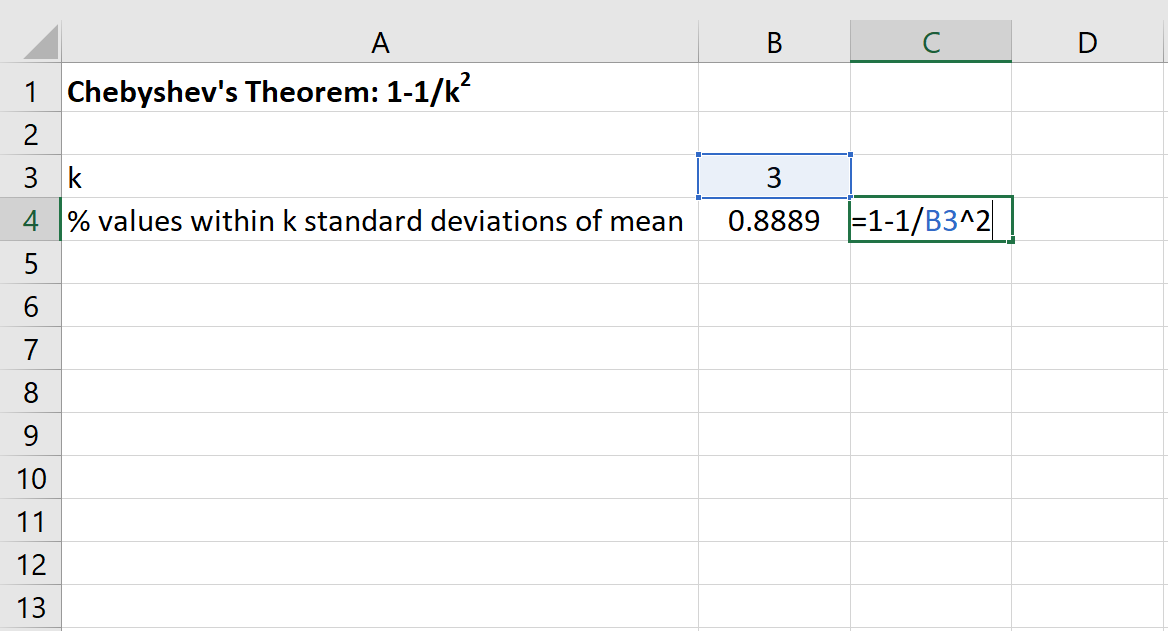
Le pourcentage de valeurs comprises entre 20 et 50 pour cet ensemble de données sera d’au moins 88,89 % .

Exemple 3 : utilisez le théorème de Chebyshev pour déterminer quel pourcentage de valeurs se situera entre 80 et 120 pour un ensemble de données avec une moyenne de 100 et un écart type de 5.

Tout d’abord, déterminez la valeur de k. Nous pouvons le faire en déterminant combien d’écarts types se trouvent entre 80 et 120 par rapport à la moyenne :

(80 – moyenne) / écart type = (80 – 100) / 5 = -20 / 5 = -4

(120 – moyenne) / écart type = (120 – 100) / 5 = 20 / 5 = 4

Les valeurs 80 et 120 sont respectivement 4 écarts types en dessous et au-dessus de la moyenne. Ainsi, k = 4 .

Nous pouvons ensuite utiliser la formule suivante dans Excel pour trouver le pourcentage minimum de valeurs qui se situent dans les 4 écarts types de la moyenne pour cet ensemble de données :

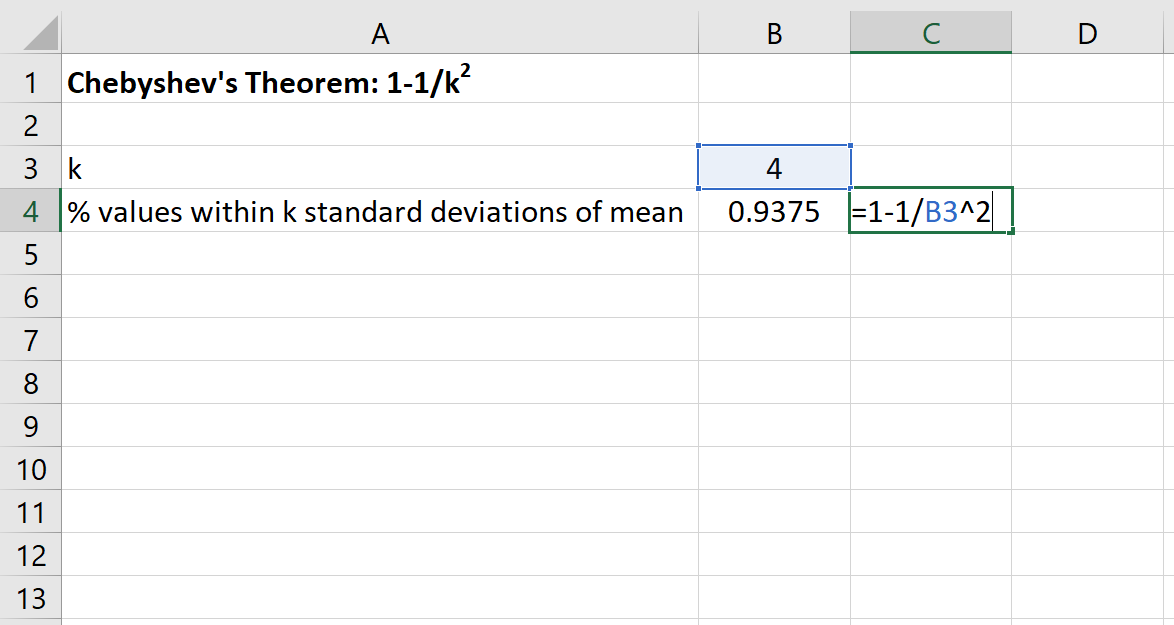
Le pourcentage de valeurs comprises entre 80 et 120 pour cet ensemble de données sera d’au moins 93,75 % .