Une introduction à la distribution binomiale

La distribution binomiale est l’une des distributions les plus populaires en statistique. Pour comprendre la distribution binomiale, il est utile de commencer par comprendre les expériences binomiales .

Expériences binomiales

Une expérience binomiale est une expérience qui possède les propriétés suivantes :

• L’expérience consiste en n essais répétés.
• Chaque essai n’a que deux résultats possibles.
• La probabilité de succès, notée p , est la même pour chaque essai.
• Chaque essai est indépendant.

L’exemple le plus évident d’une expérience binomiale est un tirage au sort. Par exemple, supposons que nous lançons une pièce 10 fois. Il s’agit d’une expérience binomiale car elle possède les quatre propriétés suivantes :

• L’expérience consiste en n essais répétés – Il y a 10 essais.
• Chaque essai n’a que deux résultats possibles : pile ou face.
• La probabilité de succès, notée p , est la même pour chaque essai. Si l’on définit le « succès » comme le fait d’arriver sur face, alors la probabilité de succès est exactement de 0,5 pour chaque essai.
• Chaque essai est indépendant – Le résultat d’un tirage au sort n’affecte pas le résultat de tout autre tirage au sort.

La distribution binomiale

La distribution binomiale décrit la probabilité d’obtenir k succès dans n expériences binomiales.

Si une variable aléatoire X suit une distribution binomiale, alors la probabilité que X = k succès peut être trouvée par la formule suivante :

P(X=k) = _n C _k * p ^k * (1-p) ^nk

où:

• n : nombre d’essais
• k : nombre de réussites
• p : probabilité de succès sur un essai donné
• _n C _k : le nombre de façons d’obtenir k succès dans n essais

Par exemple, supposons que nous lançons une pièce 3 fois. Nous pouvons utiliser la formule ci-dessus pour déterminer la probabilité d’obtenir 0, 1, 2 et 3 face lors de ces 3 lancers :

P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125

P(X=1) = ₃ C ₁ * 0,5 ¹ * (1-0,5) ^3-1 = 3 * 0,5 * (0,5) ² = 0,375

P(X=2) = ₃ C ₂ * 0,5 ² * (1-0,5) ^3-2 = 3 * 0,25 * (0,5) ¹ = 0,375

P(X=3) = ₃ C ₃ * 0,5 ³ * (1-0,5) ^3-3 = 1 * 0,125 * (0,5) ⁰ = 0,125

Remarque : Nous avons utilisé cette calculatrice combinée pour calculer _n C _k pour chaque exemple.

Nous pouvons créer un histogramme simple pour visualiser cette distribution de probabilité :

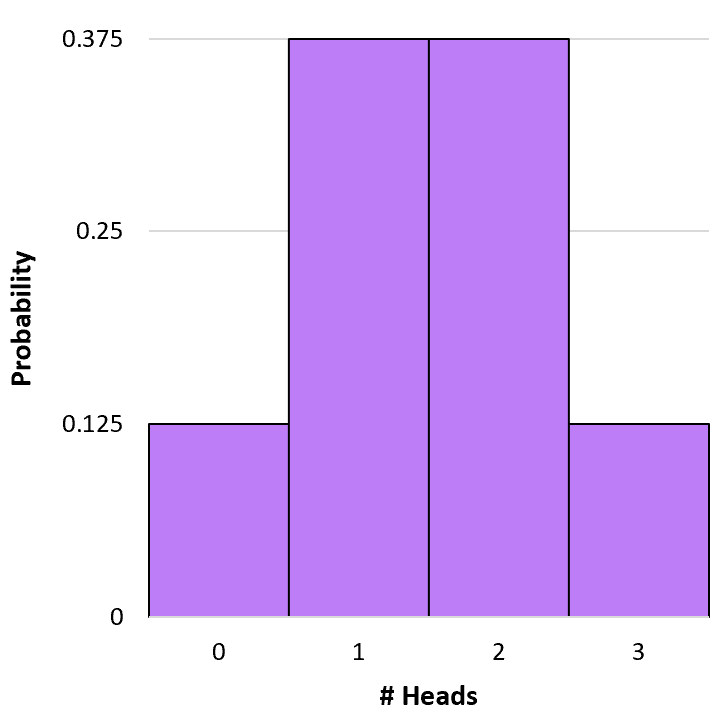
Calcul des probabilités binomiales cumulées

Il est simple de calculer une seule probabilité binomiale (par exemple la probabilité qu’une pièce tombe sur face 1 fois sur 3 lancers) en utilisant la formule ci-dessus, mais pour calculer les probabilités binomiales cumulées, nous devons ajouter des probabilités individuelles.

Par exemple, supposons que nous voulions connaître la probabilité qu’une pièce tombe sur face 1 fois ou moins sur 3 lancers. Nous utiliserions la formule suivante pour calculer cette probabilité :

P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .

C’est ce qu’on appelle une probabilité cumulative car elle implique l’ajout de plusieurs probabilités. Nous pouvons calculer la probabilité cumulée d’obtenir k face ou moins pour chaque résultat en utilisant une formule similaire :

P(X≤0) = P(X=0) = 0,125 .

P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .

P(X≤2) = P(X=0) + P(X=1) + P(X=2) = 0,125 + 0,375 + 0,375 = 0,875 .

P(X≤3) = P(X=0) + P(X=1) + P(X=2) + P(X=3) = 0,125 + 0,375 + 0,375 + 0,125 = 1 .

Nous pouvons créer un histogramme pour visualiser cette distribution de probabilité cumulée :

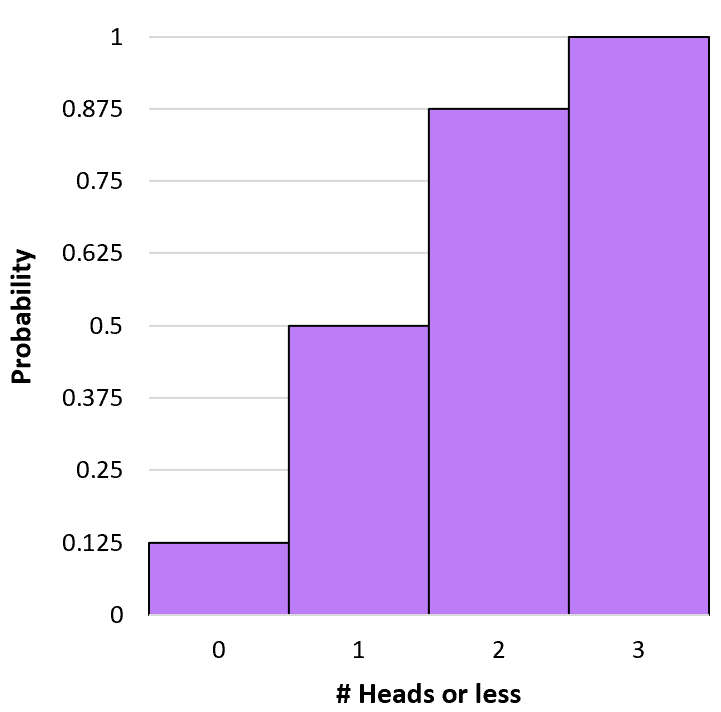
Calculateur de probabilité binomiale

Lorsque nous travaillons avec de petits nombres (par exemple 3 lancers de pièces), il est raisonnable de calculer les probabilités binomiales à la main. Cependant, lorsque nous travaillons avec des nombres plus grands (par exemple 100 tirages au sort), il peut être fastidieux de calculer les probabilités à la main. Dans ces cas, il peut être utile d’utiliser un calculateur de probabilité binomiale comme celui ci-dessous.

Par exemple, supposons que nous lançons une pièce n = 100 fois, la probabilité qu’elle atterrisse sur face dans un essai donné est p = 0,5, et nous voulons connaître la probabilité qu’elle atterrisse sur face k = 43 fois ou moins :

Voici comment interpréter le résultat :

• La probabilité que la pièce tombe sur face exactement 43 fois est de 0,03007 .
• La probabilité que la pièce tombe sur face moins de 43 fois est de 0,06661 .
• La probabilité que la pièce tombe sur face 43 fois ou moins est de 0,09667 .
• La probabilité que la pièce tombe sur face plus de 43 fois est de 0,90333 .
• La probabilité que la pièce tombe sur face 43 fois ou plus est de 0,93339 .

Propriétés de la distribution binomiale

La distribution binomiale a les propriétés suivantes :

La moyenne de la distribution est μ = np

La variance de la distribution est σ ² = np(1-p)

L’écart type de la distribution est σ = √ np(1-p)

Par exemple, supposons que nous lançons une pièce de monnaie 3 fois. Soit p = la probabilité que la pièce tombe sur face.

Le nombre moyen de têtes auquel nous nous attendons est μ = np = 3*.5 = 1.5 .

La variance du nombre de têtes à laquelle nous nous attendons est σ ² = np(1-p) = 3*.5*(1-.5) = 0.75 .

Problèmes de pratique de distribution binomiale

Utilisez les problèmes pratiques suivants pour tester vos connaissances sur la distribution binomiale.

Problème 1

Question : Bob réussit 60 % de ses tentatives de lancer franc. S’il réussit 12 lancers francs, quelle est la probabilité qu’il en réalise exactement 10 ?

Réponse : En utilisant le calculateur de distribution binomiale ci-dessus avec p = 0,6, n = 12 et k = 10, nous constatons que P(X=10) = 0,06385 .

Problème 2

Question : Jessica lance une pièce 5 fois. Quelle est la probabilité que la pièce tombe sur face 2 fois ou moins ?

Réponse : En utilisant le calculateur de distribution binomiale ci-dessus avec p = 0,5, n = 5 et k = 2, nous constatons que P(X≤2) = 0,5 .

Problème 3

Question : La probabilité qu’un étudiant donné soit accepté dans un certain collège est de 0,2. Si 10 étudiants postulent, quelle est la probabilité que plus de 4 soient acceptés ?

Réponse : En utilisant le calculateur de distribution binomiale ci-dessus avec p = 0,2, n = 10 et k = 4, nous constatons que P(X>4) = 0,03279 .

Problème 4

Question : Vous lancez une pièce 12 fois. Quel est le nombre moyen attendu de têtes qui apparaîtront ?

Réponse : Rappelons que la moyenne d’une distribution binomiale est calculée comme μ = np. Ainsi, μ = 12*0,5 = 6 têtes .

Problème 5

Question : Mark réussit un home run pendant 10 % de ses tentatives. S’il réussit 5 tentatives dans un match donné, quelle est la variance du nombre de circuits qu’il réussira ?

Réponse : Rappelons que la variance d’une distribution binomiale est calculée comme σ ² = np(1-p). Ainsi, σ ² = 6*.1*(1-.1) = 0.54 .

Ressources additionnelles

Les articles suivants peuvent vous aider à apprendre à utiliser la distribution binomiale dans différents logiciels statistiques :

• Comment calculer les probabilités binomiales dans Excel
• Comment calculer les probabilités binomiales sur une calculatrice TI-84
• Comment calculer les probabilités binomiales dans R
• Comment tracer une distribution binomiale dans R