Comment calculer les probabilités binomiales sur une calculatrice TI-84
La distribution binomiale est l’une des distributions les plus couramment utilisées dans toutes les statistiques. Ce didacticiel explique comment utiliser les fonctions suivantes sur une calculatrice TI-84 pour trouver des probabilités binomiales :
binompdf(n, p, x) renvoie la probabilité associée au pdf binomial.
binomcdf(n, p, x) renvoie la probabilité cumulée associée au cdf binomial.
où:
- n = nombre d’essais
- p = probabilité de succès sur un essai donné
- x = nombre total de réussites
Ces deux fonctions sont accessibles sur une calculatrice TI-84 en appuyant sur 2nd puis en appuyant sur vars . Cela vous amènera à un écran DISTR où vous pourrez ensuite utiliser binompdf() et binomcdf() :
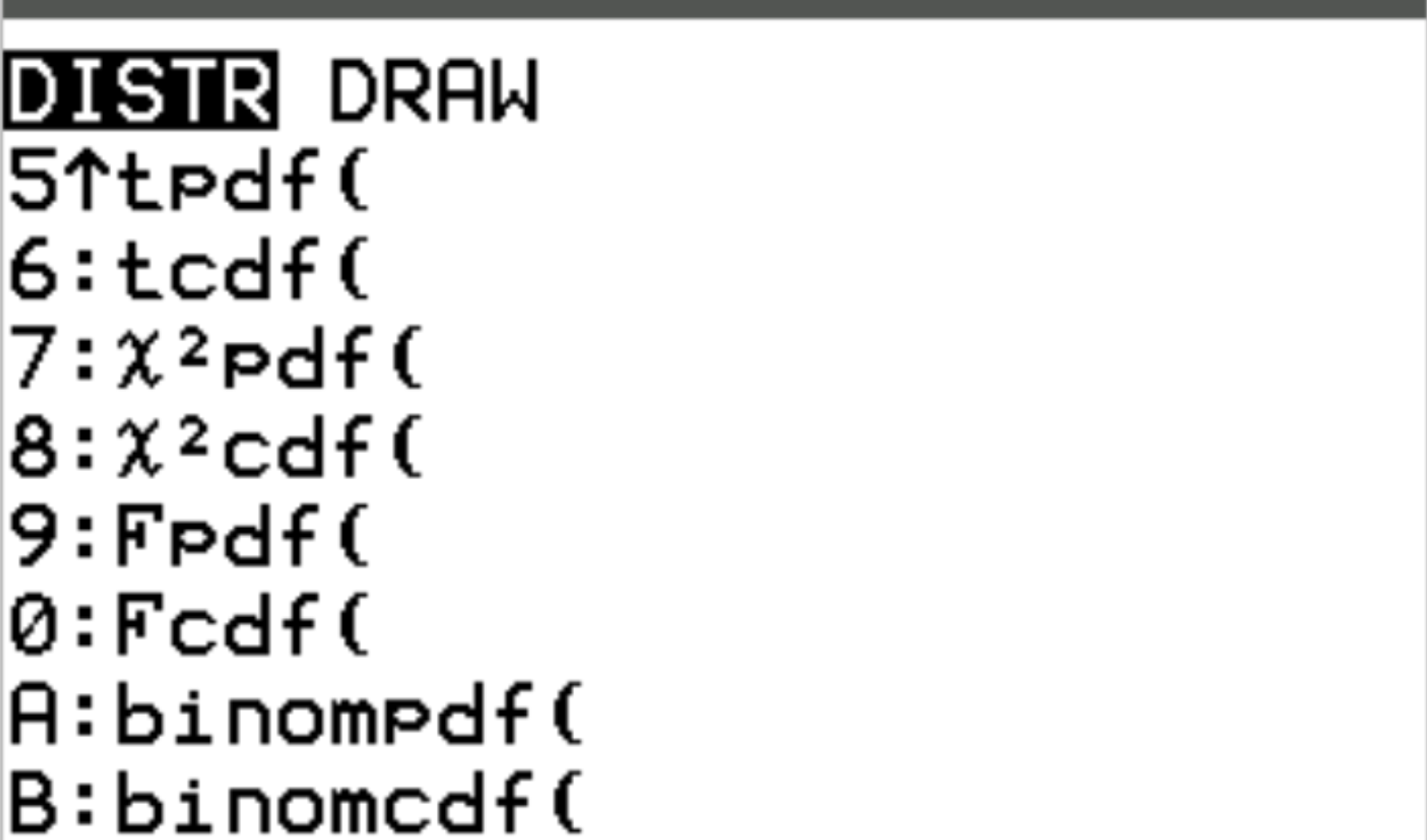
Les exemples suivants illustrent comment utiliser ces fonctions pour répondre à différentes questions.
Exemple 1 : probabilité binomiale d’exactement x succès
Question : Nathan réussit 60 % de ses tentatives de lancer franc. S’il réussit 12 lancers francs, quelle est la probabilité qu’il en réalise exactement 10 ?
Réponse : Utilisez la fonction binomialpdf(n, p, x) :
binômepdf(12, .60, 10) = 0,0639
Exemple 2 : probabilité binomiale de moins de x succès
Question : Nathan réussit 60 % de ses tentatives de lancer franc. S’il réussit 12 lancers francs, quelle est la probabilité qu’il en réalise moins de 10 ?
Réponse : Utilisez la fonction binomialcdf(n, p, x-1) :
binomialcdf(12, .60, 9) = 0,9166
Exemple 3 : probabilité binomiale d’au plus x succès
Question : Nathan réussit 60 % de ses tentatives de lancer franc. S’il réussit 12 lancers francs, quelle est la probabilité qu’il en réalise au maximum 10 ?
Réponse : Utilisez la fonction binomialcdf(n, p, x) :
binomialcdf(12, .60, 10) = 0,9804
Exemple 4 : Probabilité binomiale de plus de x succès
Question : Nathan réussit 60 % de ses tentatives de lancer franc. S’il réussit 12 lancers francs, quelle est la probabilité qu’il en réalise plus de 10 ?
Réponse : Utilisez la fonction 1 – binomialcdf(n, p, x) :
1 – binomialcdf(12, .60, 10) = 0,0196
Exemple 5 : Probabilité binomiale d’au moins x succès
Question : Nathan réussit 60 % de ses tentatives de lancer franc. S’il réussit 12 lancers francs, quelle est la probabilité qu’il en réalise plus de 10 ?
Réponse : Utilisez la fonction 1 – binomialcdf(n, p, x-1) :
1 – binomialcdf(12, .60, 9) = 0,0834
