Comment effectuer une ANOVA unidirectionnelle sur une calculatrice TI-84

Une ANOVA unidirectionnelle est utilisée pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes indépendants ou plus.

Ce didacticiel explique comment effectuer une ANOVA unidirectionnelle sur une calculatrice TI-84.

Exemple : ANOVA unidirectionnelle sur une calculatrice TI-84

Supposons que nous recrutions 30 étudiants pour participer à une étude. Les étudiants sont assignés au hasard à utiliser l’une des trois techniques d’étude pendant un mois pour se préparer à un examen. A la fin du mois, tous les étudiants passent le même test.

Utilisez les étapes suivantes pour effectuer une ANOVA unidirectionnelle afin de déterminer si les scores moyens sont les mêmes dans les trois groupes.

Étape 1 : Saisissez les données.

Tout d’abord, nous saisirons les valeurs des données pour la variable explicative et la variable de réponse. Appuyez sur Stat puis appuyez sur EDIT . Saisissez les résultats d’examen suivants pour les étudiants qui ont utilisé la première technique d’étude dans la colonne L1, la deuxième technique d’étude dans la colonne L2 et la troisième technique d’étude dans la colonne L3 :

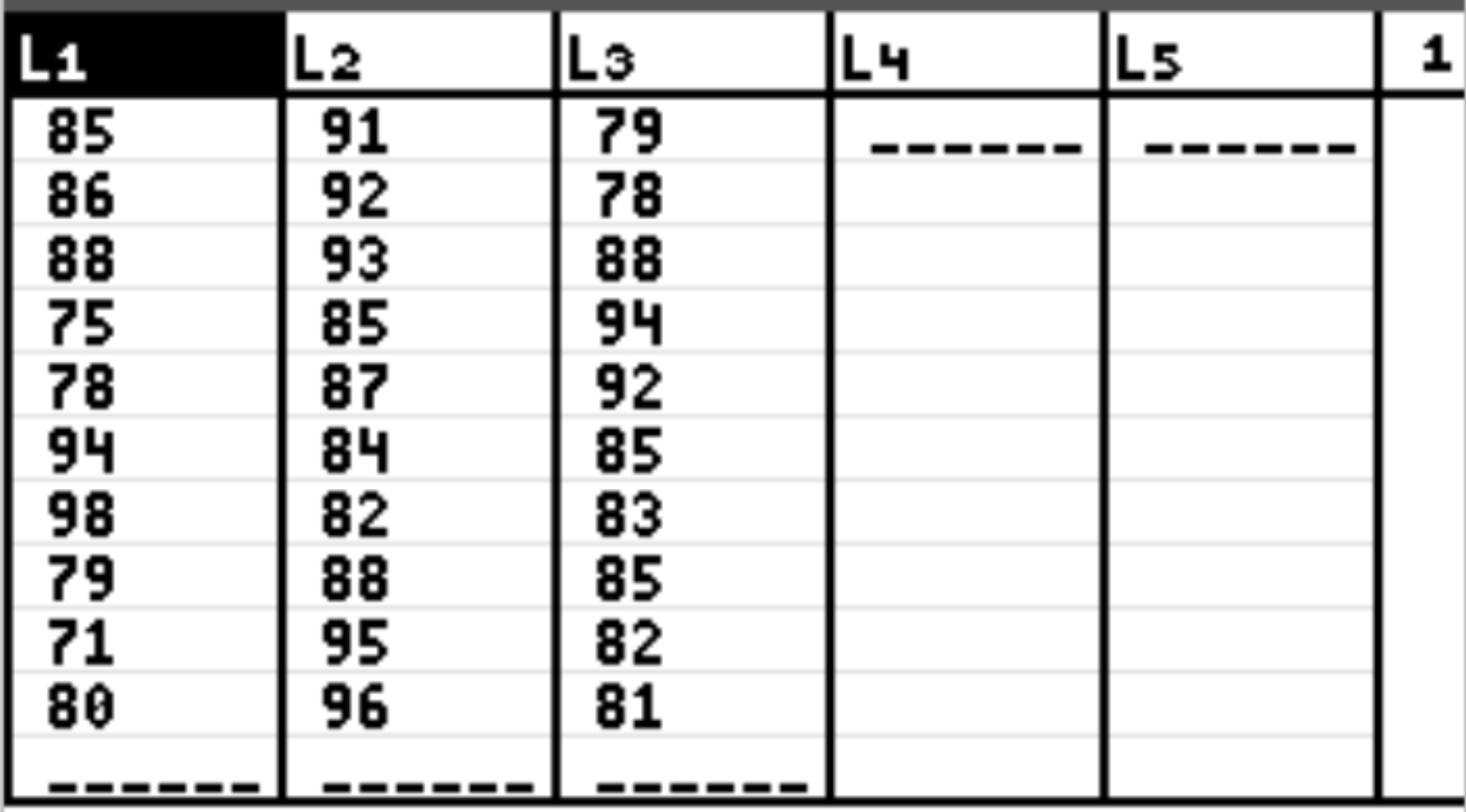
Étape 2 : Effectuez l’ANOVA unidirectionnelle.

Ensuite, nous effectuerons l’ANOVA unidirectionnelle. Appuyez sur Stat puis faites défiler jusqu’à TESTS . Faites ensuite défiler jusqu’à ANOVA et appuyez sur Entrée .

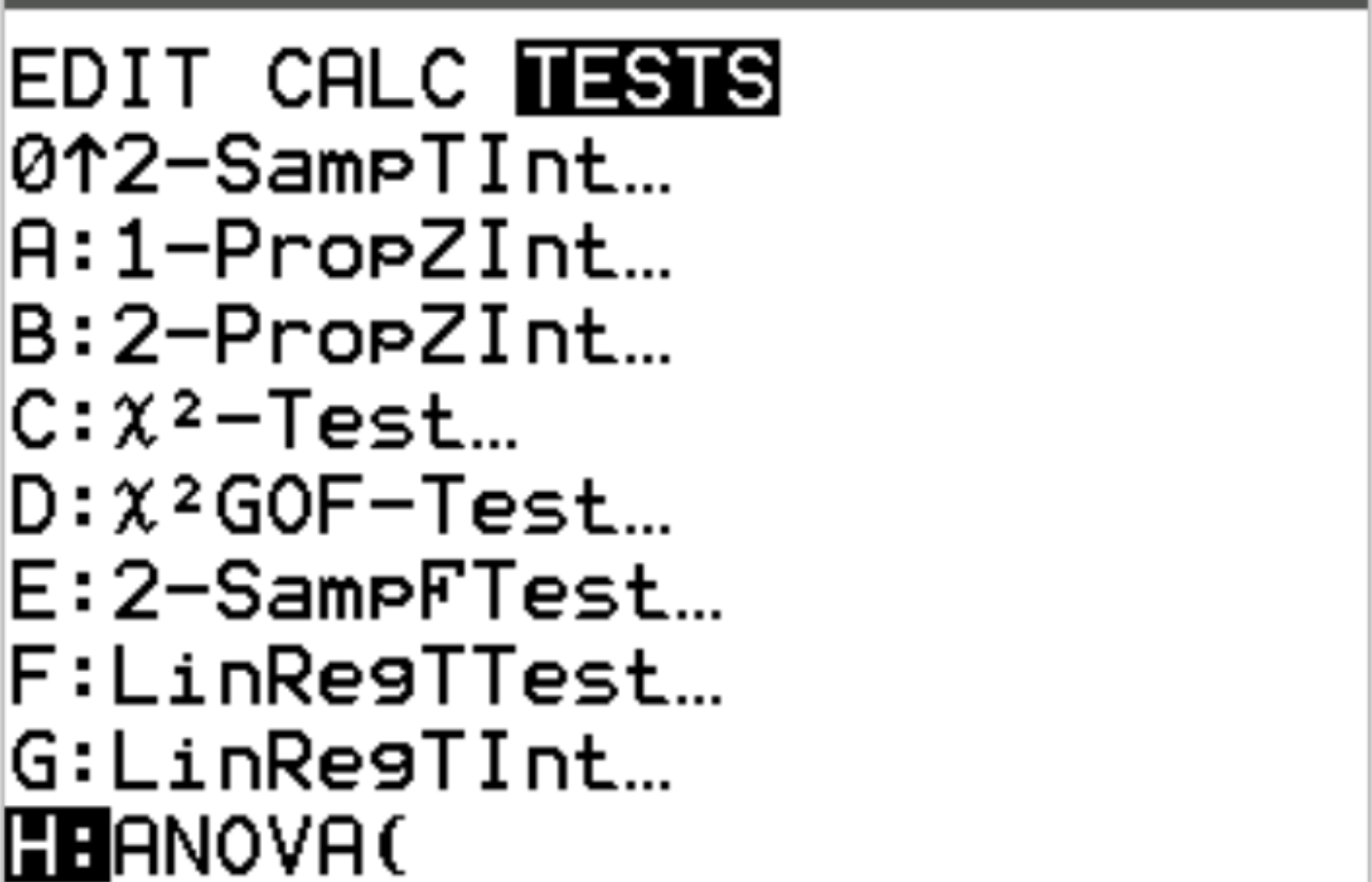
Entrez les listes où les données sont stockées séparées par des virgules, puis ajoutez une parenthèse fermante ) puis appuyez sur Entrée .

Remarque : Pour faire apparaître L1, appuyez sur 2 , puis appuyez sur 1 . Pour faire apparaître L2, appuyez sur 2nd puis appuyez sur 2 . Pour faire apparaître L3, appuyez sur 2ème puis appuyez sur 3 .

Les résultats suivants apparaîtront une fois que vous appuierez sur Entrée :

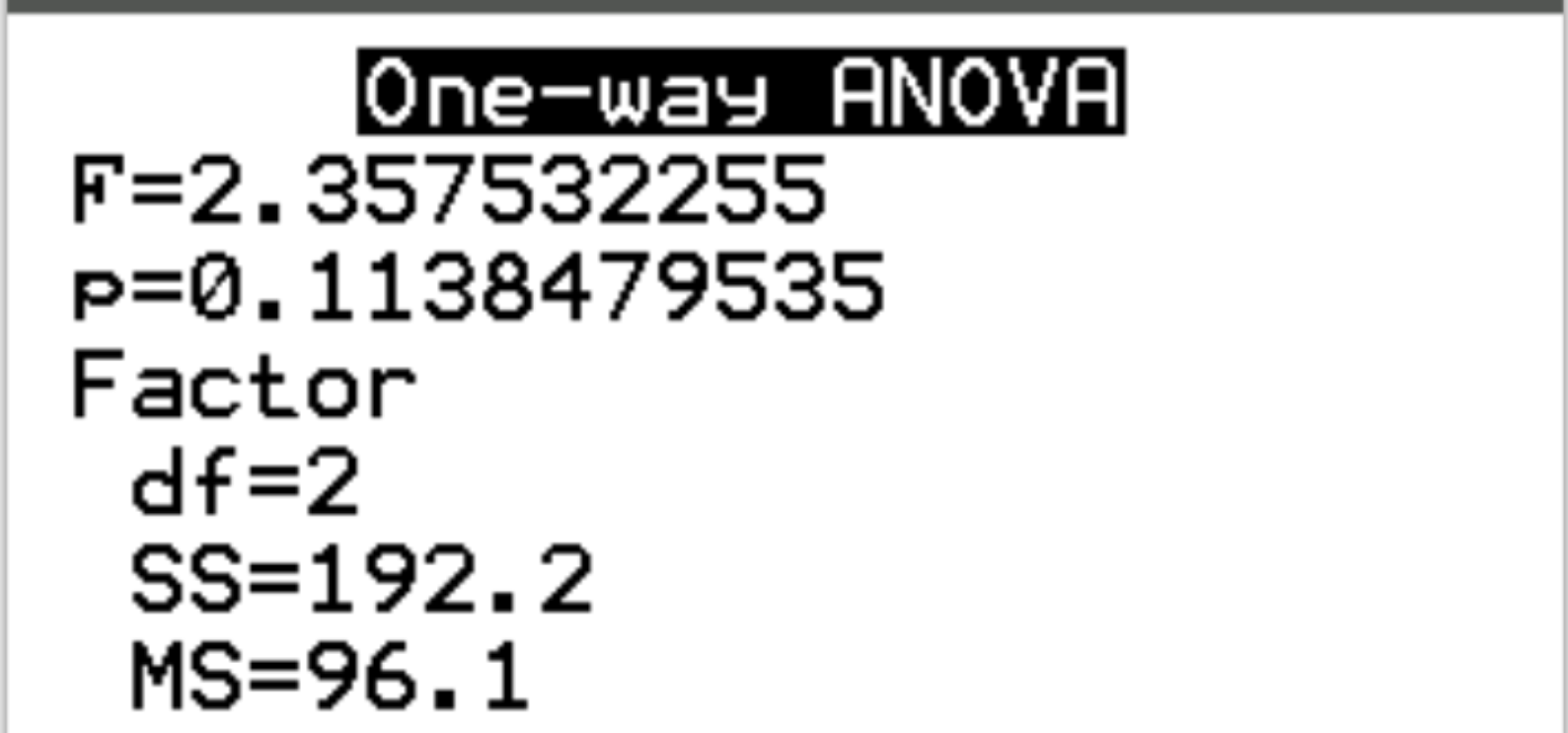
Étape 3 : Interprétez les résultats.

La statistique F du test est de 2,3575 et la valeur p correspondante est de 0,1138 . Puisque cette valeur p n’est pas inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle.

Nous ne disposons donc pas de preuves suffisantes pour affirmer que la note moyenne à l’examen est différente entre les trois groupes. Autrement dit, nous n’avons pas suffisamment de preuves pour affirmer que la technique d’étude conduit à des résultats d’examen différents.