Que sont les variables aléatoires ?

Une variable aléatoire , généralement notée X, est une variable dont les valeurs possibles sont les résultats d’un processus aléatoire.

Il existe deux types de variables aléatoires : discrètes et continues .

Variables aléatoires discrètes

Une variable aléatoire discrète est une variable qui ne peut prendre qu’un nombre dénombrable de valeurs distinctes comme 0, 1, 2, 3, 4, 5…100, 1 million, etc. Voici quelques exemples de variables aléatoires discrètes :

• Le nombre de fois qu’une pièce tombe sur pile après avoir été lancée 20 fois.
• Le nombre de fois qu’un dé atterrit sur le chiffre 4 après avoir été lancé 100 fois.
• Le nombre de widgets défectueux dans une boîte de 50 widgets.

Une distribution de probabilité pour une variable aléatoire discrète nous indique la probabilité que la variable aléatoire prenne certaines valeurs.

Par exemple, supposons que nous lançons un dé équitable une fois. Si nous laissons X désigner la probabilité que le dé tombe sur un certain nombre, alors la distribution de probabilité peut s’écrire comme suit :

• P(X=1) : 1/6
• P(X=2) : 1/6
• P(X=3) : 1/6
• P(X=4) : 1/6
• P(X=5) : 1/6
• P(X=6) : 1/6

Note:

Pour qu’une distribution de probabilité soit valide, elle doit satisfaire aux deux critères suivants :

1. La probabilité de chaque résultat doit être comprise entre 0 et 1.

2. La somme de toutes les probabilités doit totaliser 1.

Notez que la distribution de probabilité pour le lancer de dé satisfait à ces deux critères :

1. La probabilité de chaque résultat est comprise entre 0 et 1.

2. La somme de toutes les probabilités totalise 1.

Nous pouvons utiliser un histogramme pour visualiser la distribution de probabilité :

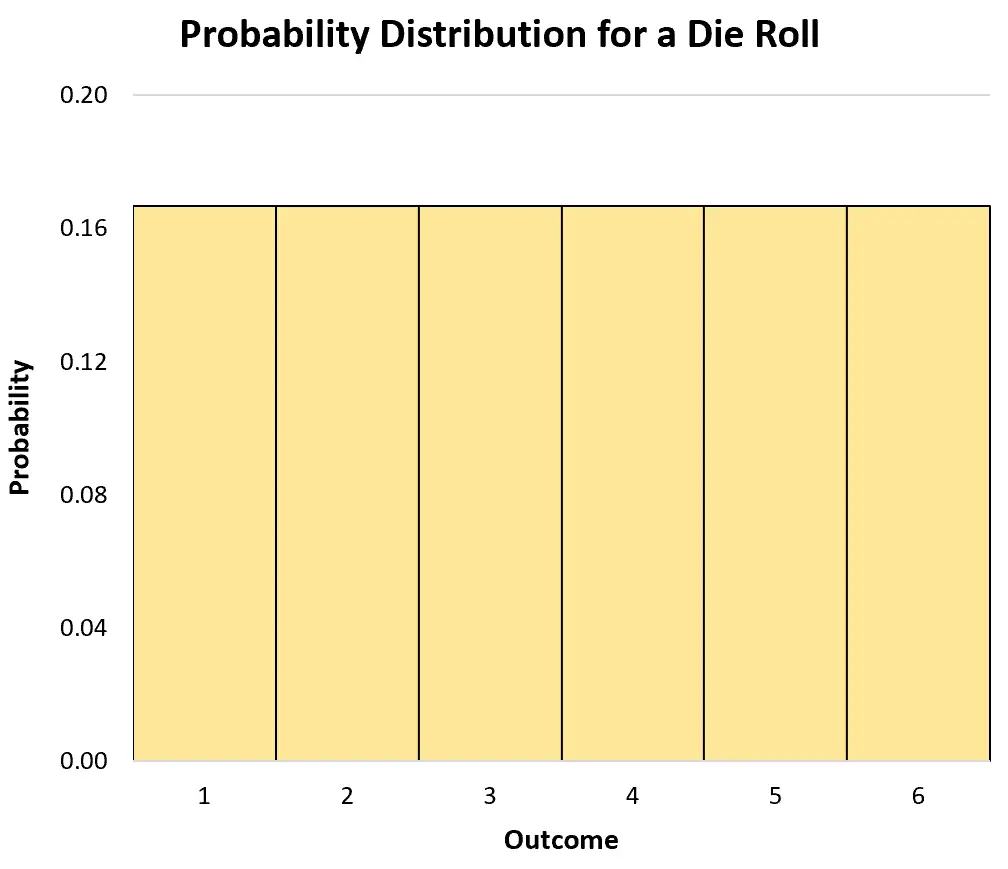
Une distribution de probabilité cumulative pour une variable aléatoire discrète nous indique la probabilité que la variable prenne une valeur égale ou inférieure à une certaine valeur.

Par exemple, la distribution de probabilité cumulée pour un lancer de dé ressemblerait à :

• P(X≤1) : 1/6
• P(X≤2) : 2/6
• P(X≤3) : 3/6
• P(X≤4) : 4/6
• P(X≤5) : 5/6
• P(X≤6) : 6/6

La probabilité que le dé atterrisse sur un ou moins est simplement de 1/6, puisqu’il ne peut pas atterrir sur un nombre inférieur à un.

La probabilité qu’il atterrisse sur deux ou moins est P(X=1) + P(X=2) = 1/6 + 1/6 = 2/6.

De même, la probabilité qu’il atterrisse sur trois ou moins est P(X=1) + P(X=2) + P(X=3) = 1/6 + 1/6 + 1/6 = 3/6, et ainsi de suite.

Nous pouvons également utiliser un histogramme pour visualiser la distribution de probabilité cumulée :

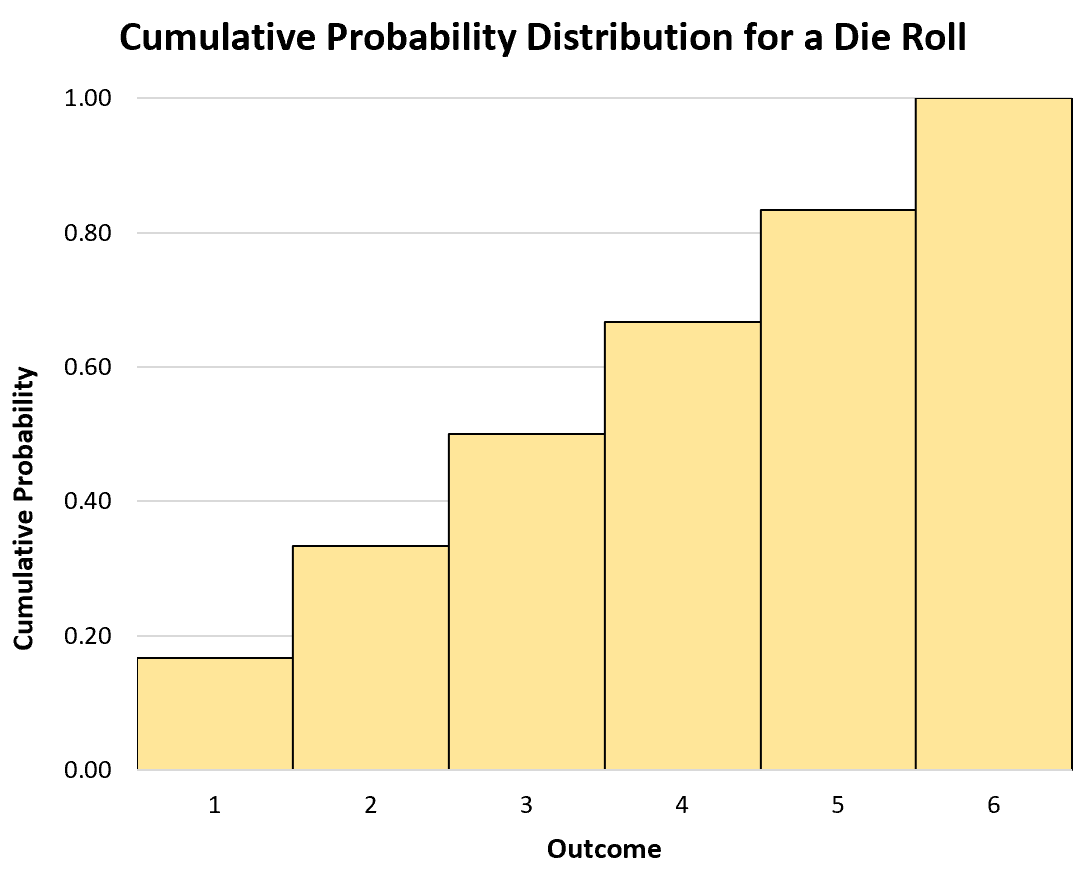
Variables aléatoires continues

Une variable aléatoire continue est une variable qui peut prendre une infinité de valeurs possibles. Voici quelques exemples de variables aléatoires continues :

• Poids d’un animal
• Taille d’une personne
• Temps nécessaire pour courir un marathon

Par exemple, la taille d’une personne peut être de 60,2 pouces, 65,2344 pouces, 70,431222 pouces, etc. Il existe une quantité infinie de valeurs possibles pour la taille.

Règle générale :

Si vous pouvez compter le nombre de résultats, alors vous travaillez avec une variable aléatoire discrète – par exemple, compter le nombre de fois qu’une pièce tombe sur face.

Mais si vous pouvez mesurer le résultat, vous travaillez avec une variable aléatoire continue – par exemple mesurer la taille, le poids, le temps, etc.

Une distribution de probabilité pour une variable aléatoire continue nous indique la probabilité que la variable aléatoire prenne certaines valeurs.

Cependant, contrairement à une distribution de probabilité pour des variables aléatoires discrètes, une distribution de probabilité pour une variable aléatoire continue ne peut être utilisée que pour nous indiquer la probabilité que la variable prenne une plage de valeurs.

Par exemple, supposons que nous souhaitions connaître la probabilité qu’un hamburger d’un restaurant particulier pèse un quart de livre (0,25 livre). Le poids étant une variable continue, il peut prendre un nombre infini de valeurs.

Par exemple, un hamburger donné peut en réalité peser 0,250001 livre, ou 0,24 livre, ou 0,2488 livre. La probabilité qu’un hamburger donné pèse exactement 0,25 livre est essentiellement nulle.

Ainsi, nous ne pouvons utiliser qu’une distribution de probabilité pour nous indiquer la probabilité qu’un hamburger pèse moins de 0,25 lb, plus de 0,25 lb ou entre une certaine fourchette (par exemple entre 0,23 lb et 0,27 lb).

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur les variables aléatoires :

Que sont les variables aléatoires iid ?
10 exemples de variables aléatoires dans la vie réelle