Comment convertir entre les scores Z et les centiles dans Excel

Un score z nous indique à combien d’écarts types une certaine valeur se trouve par rapport à la moyenne d’un ensemble de données.

Un centile nous indique quel pourcentage d’observations tombent en dessous d’une certaine valeur dans un ensemble de données.

Nous souhaitons souvent effectuer une conversion entre les scores z et les centiles, en fonction du type de question à laquelle nous essayons de répondre. Heureusement, Excel dispose de deux fonctions intégrées qui facilitent la conversion entre les deux.

Comment convertir les scores Z en centiles dans Excel

Nous pouvons utiliser la fonction Excel intégrée suivante pour convertir un score z en centile :

=NORM.S.DIST(z, cumulatif)

où:

• z = z-score d’une certaine valeur de données
• cumulative = TRUE renvoie la fonction de distribution cumulative ; FALSE renvoie la fonction de distribution de probabilité. Nous utiliserons TRUE pour calculer les centiles.

Par exemple, voici comment convertir un score z de 1,78 en centile :

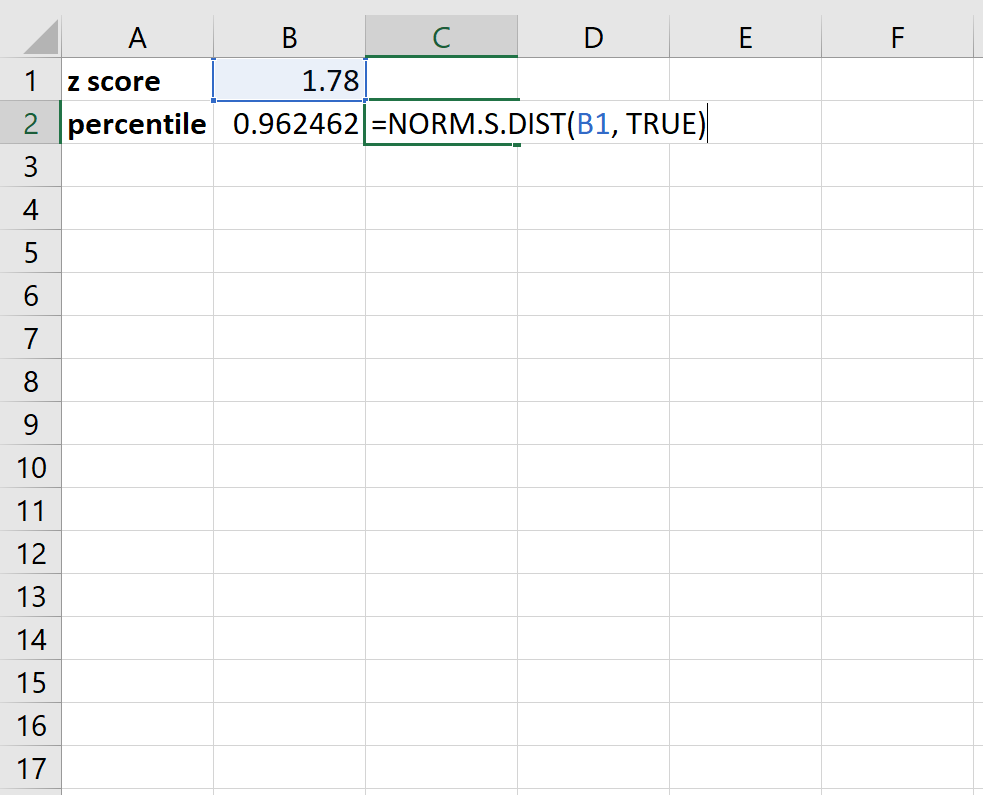
Il s’avère qu’un score z de 1,78 correspond à un percentile d’environ 96,2 . En clair, cela signifie qu’une valeur de données ayant un score z de 1,78 est supérieure à environ 96,2 % de toutes les autres valeurs de données de l’ensemble de données.

Comment convertir des centiles en scores Z dans Excel

Nous pouvons utiliser la fonction Excel intégrée suivante pour convertir un centile en score z :

=NORM.S.INV(probabilité)

où:

• probabilité = le percentile que vous souhaitez convertir.

Par exemple, voici comment convertir un percentile de 0,85 en un score z :

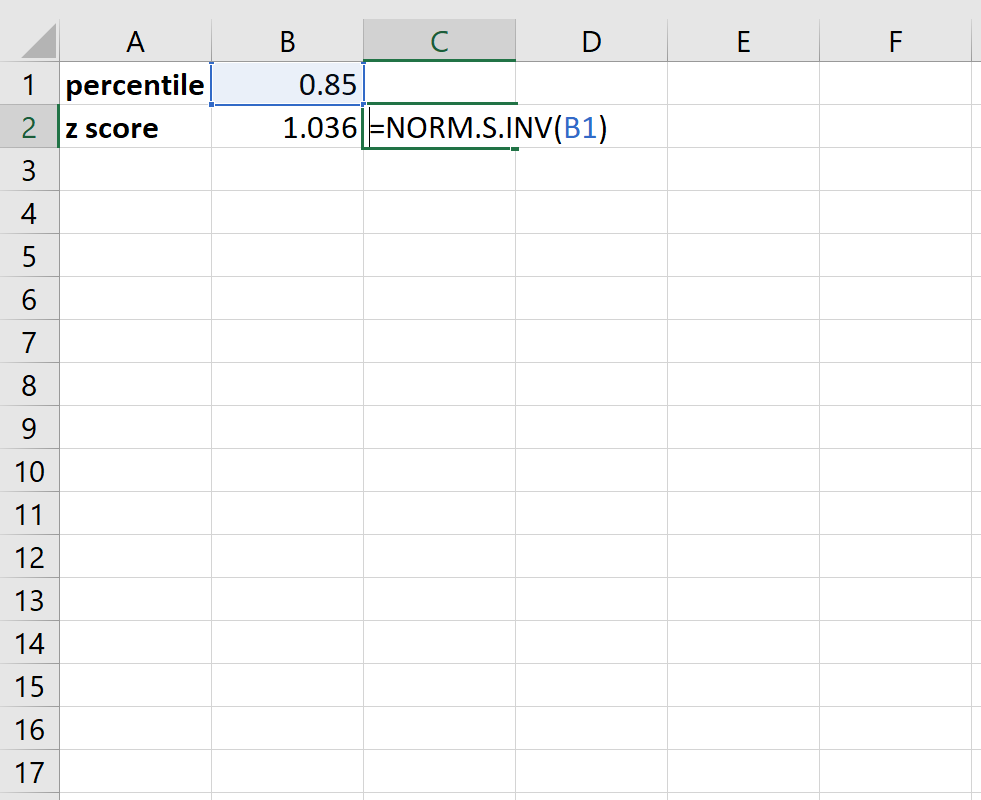
Il s’avère qu’un centile de 0,85 correspond à un score z d’environ 1,036 . En clair, cela signifie qu’une valeur de données située au 85e centile dans un ensemble de données a un score z de 1,036.

La relation entre les percentiles et les scores Z

Les scores Z peuvent prendre n’importe quelle valeur comprise entre l’infini négatif et l’infini. Toutefois, les percentiles ne peuvent prendre que des valeurs comprises entre 0 et 100.

Un score z de 0 correspond à un percentile d’exactement 0,50. Ainsi, tout z-score supérieur à 0 correspond à un centile supérieur à 0,50 et tout z-score inférieur à 0 correspond à un centile inférieur à 0,50.

Selon le type de question à laquelle vous essayez de répondre, il peut être plus utile de connaître le score z ou le centile.

Par exemple, supposons que Jessica obtienne une note de 90 % à un certain examen. Cela peut sembler un score élevé, mais que se passerait-il si l’examen était vraiment facile et que toute sa classe réussissait bien ? Pour déterminer la qualité de sa note par rapport à toutes les autres notes de la classe, nous pourrions calculer à la fois le score z et le centile de sa note à l’examen.

Si sa note à l’examen correspond à un score z de 1,23, cela signifie que sa note à l’examen était de 1,23 écart-type au-dessus de la note moyenne à l’examen. Ce score z correspond également à un centile d’environ 0,89, ce qui signifie qu’elle a obtenu un score supérieur à 89 % de ses camarades de classe. Remarquez comment le score z et le percentile nous fournissent des informations utiles sur sa note à l’examen.