Comment calculer le VIF dans Excel

La multicolinéarité dans l’analyse de régression se produit lorsque deux ou plusieurs variables explicatives sont fortement corrélées les unes aux autres, de sorte qu’elles ne fournissent pas d’informations uniques ou indépendantes dans le modèle de régression. Si le degré de corrélation est suffisamment élevé entre les variables, cela peut poser des problèmes lors de l’ajustement et de l’interprétation du modèle de régression.

Heureusement, il est possible de détecter la multicolinéarité à l’aide d’une métrique appelée facteur d’inflation de la variance (VIF) , qui mesure la corrélation et la force de la corrélation entre les variables explicatives dans un modèle de régression.

Ce tutoriel explique comment calculer VIF dans Excel.

Exemple : calcul du VIF dans Excel

Pour cet exemple, nous effectuerons une régression linéaire multiple en utilisant l’ensemble de données suivant qui décrit les attributs de 10 joueurs de basket-ball. Nous ajusterons un modèle de régression en utilisant la note comme variable de réponse et les points, les passes décisives et les rebonds comme variables explicatives. Ensuite, nous identifierons les valeurs VIF pour chaque variable explicative.

Étape 1 : Effectuez une régression linéaire multiple.

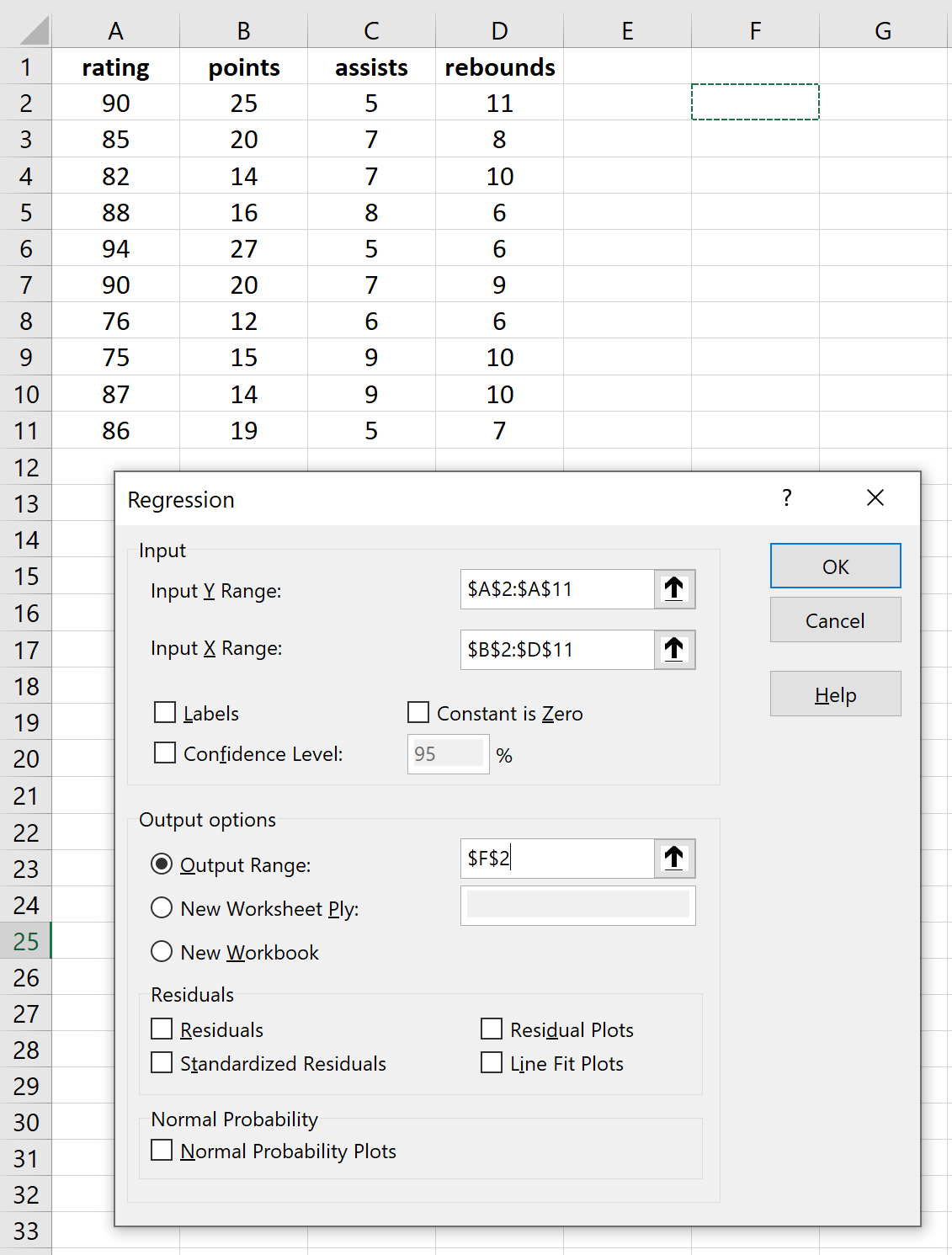
Dans le ruban supérieur, accédez à l’onglet Données et cliquez sur Analyse des données. Si vous ne voyez pas cette option, vous devez d’abord installer le logiciel gratuit Analysis ToolPak .

Une fois que vous avez cliqué sur Analyse des données, une nouvelle fenêtre apparaîtra. Sélectionnez Régression et cliquez sur OK.

Remplissez les tableaux nécessaires pour les variables de réponse et les variables explicatives, puis cliquez sur OK.

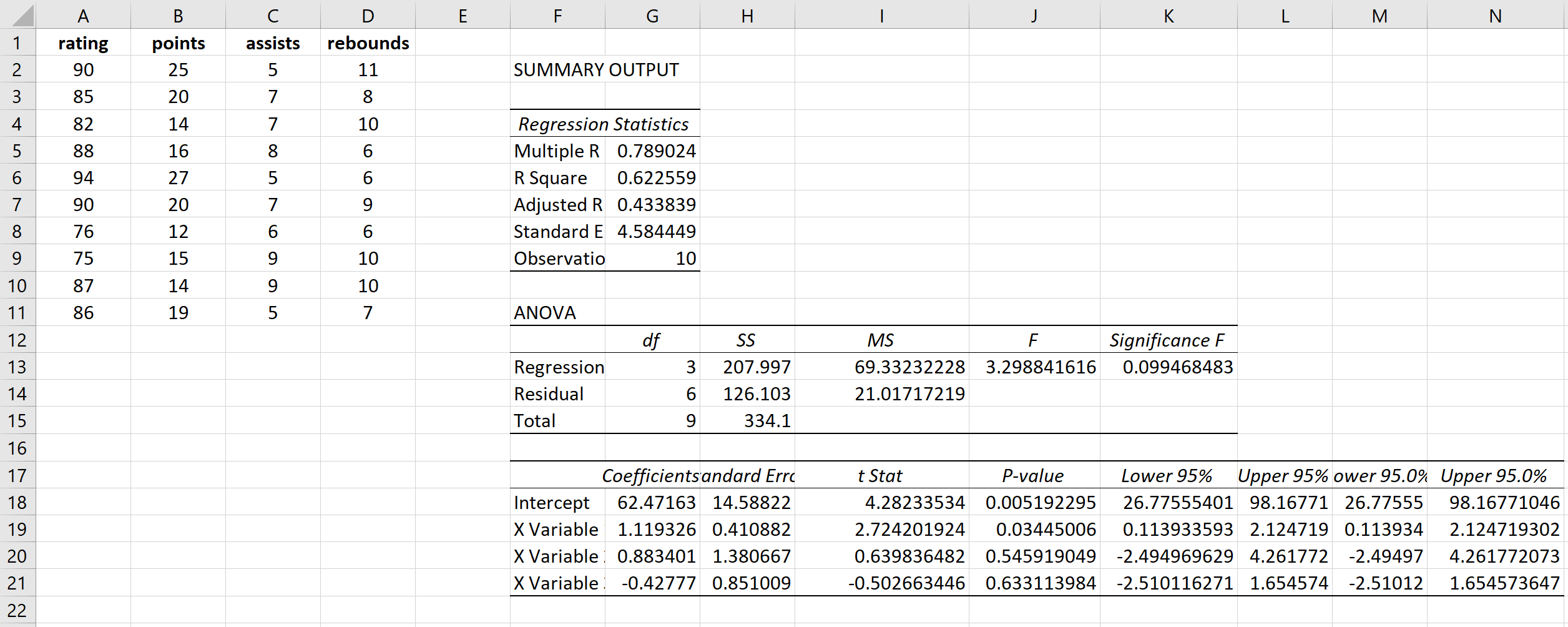
Cela produit le résultat suivant :

Étape 2 : Calculez le VIF pour chaque variable explicative.

Ensuite, nous pouvons calculer le VIF pour chacune des trois variables explicatives en effectuant des régressions individuelles en utilisant une variable explicative comme variable de réponse et les deux autres comme variables explicatives.

Par exemple, nous pouvons calculer le VIF pour la variable points en effectuant une régression linéaire multiple en utilisant les points comme variable de réponse et les assistances et les rebonds comme variables explicatives.

Cela produit le résultat suivant :

Le VIF pour les points est calculé comme 1 / (1 – R Square) = 1 / (1 – .433099) = 1,76 .

Nous pouvons ensuite répéter ce processus pour les deux autres variables, passes décisives et rebonds .

Il s’avère que les VIF pour les trois variables explicatives sont les suivants :

points : 1,76
passes décisives : 1,96
rebonds : 1,18

Comment interpréter les valeurs VIF

La valeur de VIF commence à 1 et n’a pas de limite supérieure. Une règle générale pour interpréter les VIF est la suivante :

• Une valeur de 1 indique qu’il n’y a aucune corrélation entre une variable explicative donnée et toute autre variable explicative du modèle.
• Une valeur comprise entre 1 et 5 indique une corrélation modérée entre une variable explicative donnée et d’autres variables explicatives du modèle, mais elle n’est souvent pas suffisamment grave pour nécessiter une attention particulière.
• Une valeur supérieure à 5 indique une corrélation potentiellement sévère entre une variable explicative donnée et d’autres variables explicatives du modèle. Dans ce cas, les estimations des coefficients et les valeurs p dans les résultats de la régression ne sont probablement pas fiables.

Étant donné que chacune des valeurs VIF des variables explicatives de notre modèle de régression est proche de 1, la multicolinéarité n’est pas un problème dans notre exemple.