Comment tester la normalité dans Stata

De nombreux tests statistiques nécessitent qu’une ou plusieurs variables soient distribuées normalement pour que les résultats du test soient fiables.

Ce didacticiel explique plusieurs méthodes que vous pouvez utiliser pour tester la normalité entre les variables dans Stata.

Pour chacune de ces méthodes, nous utiliserons l’ensemble de données Stata intégré appelé auto . Vous pouvez charger cet ensemble de données à l’aide de la commande suivante :

utilisation automatique du système

Méthode 1 : histogrammes

Une façon informelle de voir si une variable est normalement distribuée consiste à créer un histogramme pour afficher la distribution de la variable.

Si la variable est distribuée normalement, l’histogramme doit prendre la forme d’une « cloche » avec plus de valeurs situées près du centre et moins de valeurs situées sur les queues.

Nous pouvons utiliser la commande hist pour créer un histogramme pour le déplacement variable :

déplacement de l’hist

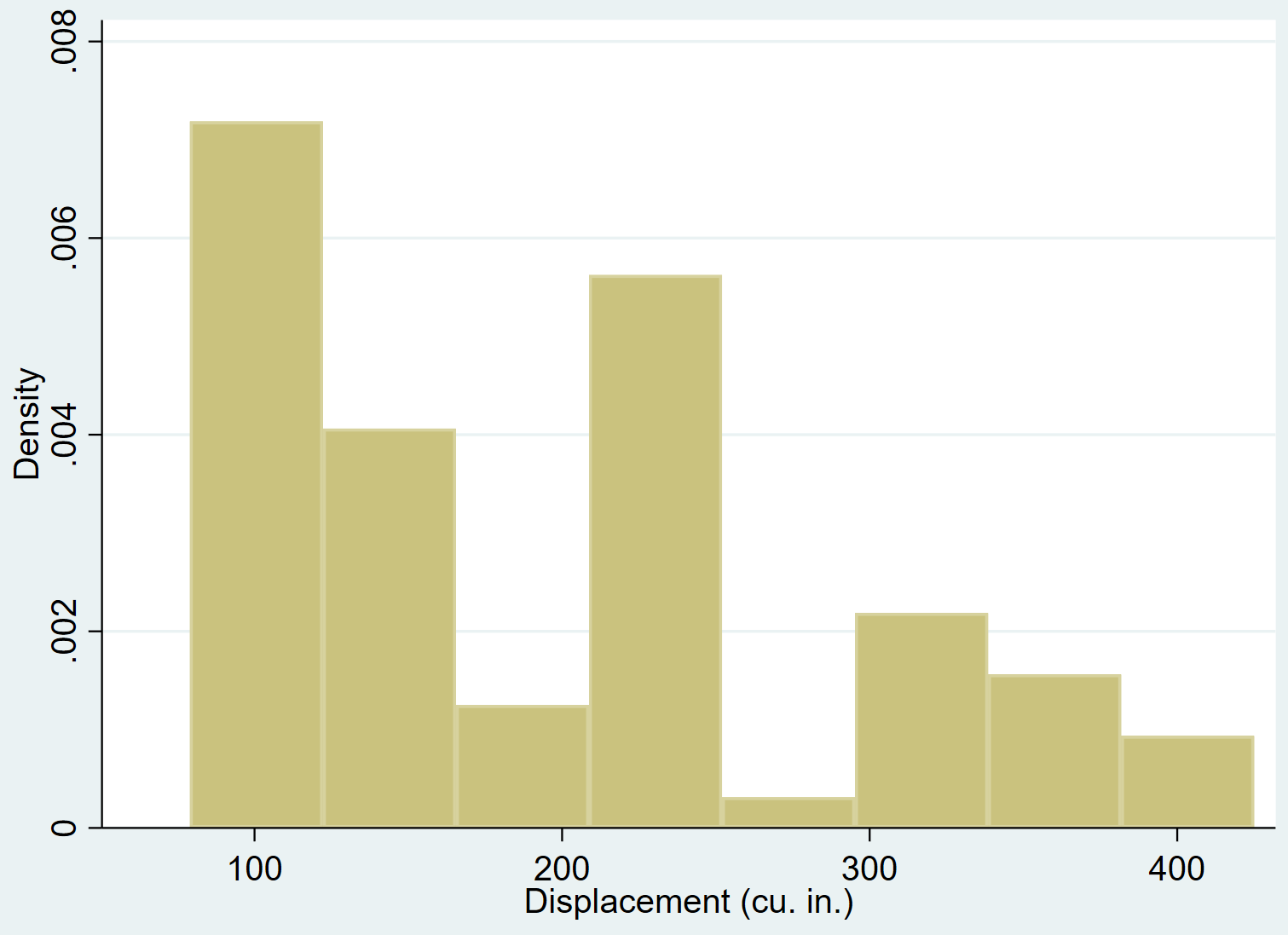
Nous pouvons ajouter une courbe de densité normale à un histogramme en utilisant la commande normale :

déplacement de l’hist, normal

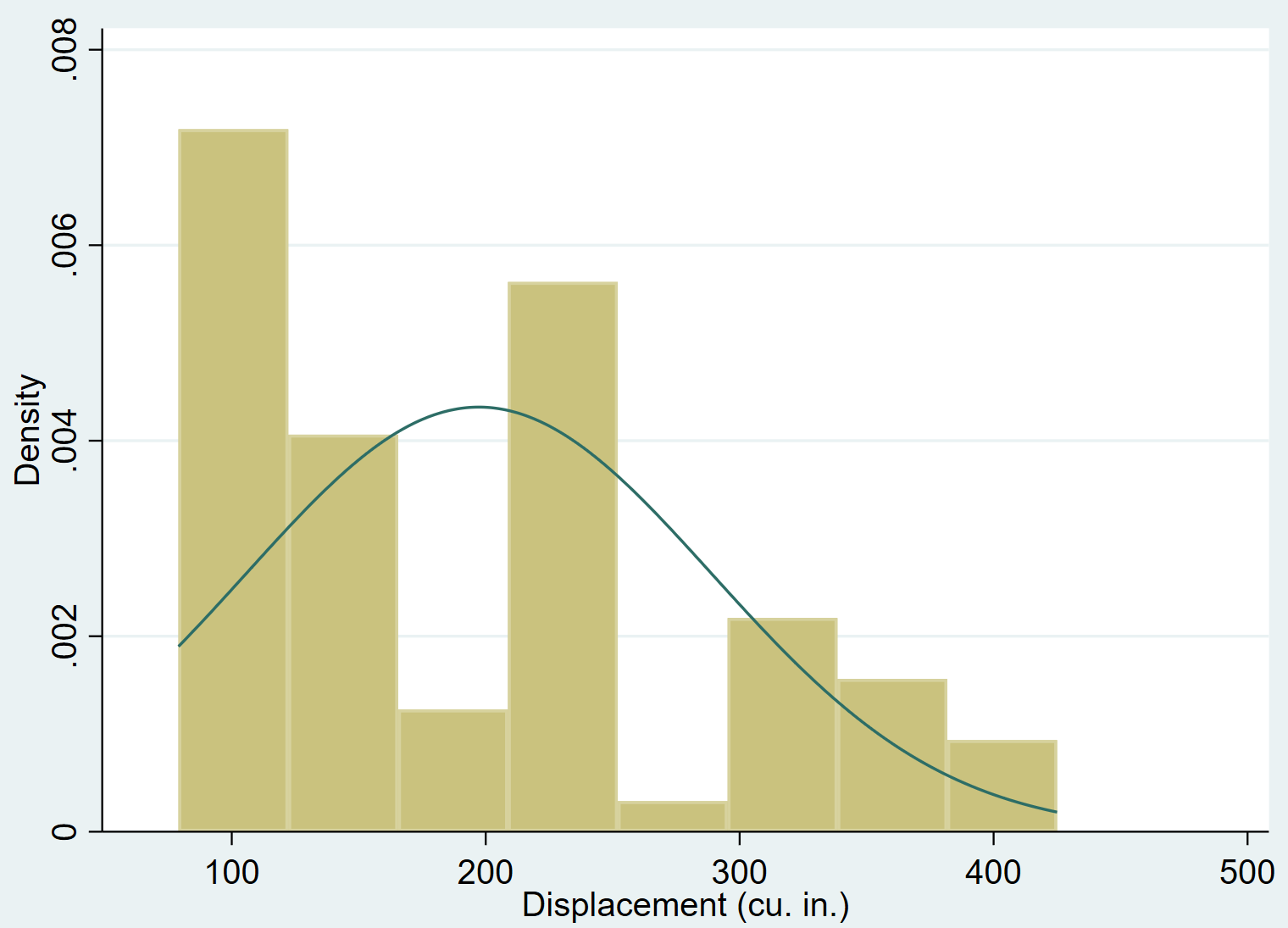
Il est assez évident que le déplacement variable est asymétrique vers la droite (par exemple la plupart des valeurs sont concentrées à gauche et une longue « queue » de valeurs s’étend vers la droite) et ne suit pas une distribution normale.

Connexes : Distributions asymétriques à gauche et à droite

Méthode 2 : test de Shapiro-Wilk

Un moyen formel de tester la normalité consiste à utiliser le test de Shapiro-Wilk .

L’hypothèse nulle pour ce test est que la variable est normalement distribuée. Si la valeur p du test est inférieure à un certain niveau de signification (les choix courants incluent 0,01, 0,05 et 0,10), nous pouvons alors rejeter l’hypothèse nulle et conclure qu’il existe suffisamment de preuves pour affirmer que la variable n’est pas distribuée normalement.

*Ce test peut être utilisé lorsque le nombre total d’observations est compris entre 4 et 2 000.

Nous pouvons utiliser la commande swilk pour effectuer un test Shapiro-Wilk sur la cylindrée variable :

déplacement fluide

Voici comment interpréter le résultat du test :

Obs : 74. C’est le nombre d’observations utilisées dans le test.

W : 0,92542. Il s’agit de la statistique de test pour le test.

Prob>z : 0,00031. Il s’agit de la valeur p associée à la statistique de test.

Puisque la valeur p est inférieure à 0,05, nous pouvons rejeter l’hypothèse nulle du test. Nous avons suffisamment de preuves pour affirmer que le déplacement variable n’est pas normalement distribué.

Nous pouvons également effectuer le test Shapiro-Wilk sur plusieurs variables à la fois en listant plusieurs variables après la commande swilk :

longueur mpg de cylindrée swilk

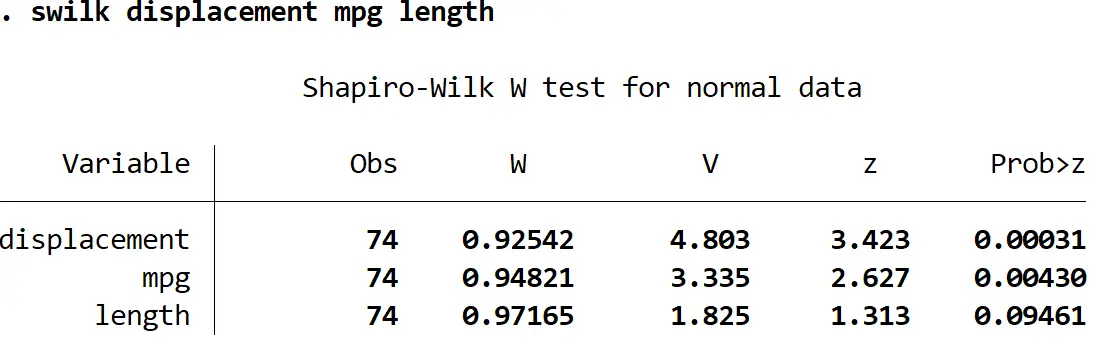
En utilisant un niveau de signification de 0,05, nous conclurions que le déplacement et le mpg ne sont pas distribués normalement, mais nous n’avons pas suffisamment de preuves pour affirmer que la longueur n’est pas distribuée normalement.

Méthode 3 : Test Shapiro-Francia

Une autre façon formelle de tester la normalité consiste à utiliser le test de Shapiro-Francia .

L’hypothèse nulle pour ce test est que la variable est normalement distribuée. Si la valeur p du test est inférieure à un certain niveau de signification, nous pouvons alors rejeter l’hypothèse nulle et conclure qu’il existe suffisamment de preuves pour affirmer que la variable n’est pas distribuée normalement.

*Ce test peut être utilisé lorsque le nombre total d’observations est compris entre 10 et 5 000.

On peut utiliser la commande sfrancia pour effectuer un Test Shapiro-Wilk sur la cylindrée variable :

déplacement sfrancia

Voici comment interpréter le résultat du test :

Obs : 74. C’est le nombre d’observations utilisées dans le test.

W’ : 0,93011. Il s’agit de la statistique de test pour le test.

Prob>z : 0,00094. Il s’agit de la valeur p associée à la statistique de test.

Puisque la valeur p est inférieure à 0,05, nous pouvons rejeter l’hypothèse nulle du test. Nous avons suffisamment de preuves pour affirmer que le déplacement variable n’est pas normalement distribué.

Semblable au test Shapiro-Wilk, vous pouvez effectuer le test Shapiro-Francia sur plusieurs variables à la fois en répertoriant plusieurs variables après la commande sfrancia .

Méthode 4 : test d’asymétrie et d’aplatissement

Une autre façon de tester la normalité consiste à utiliser le test d’asymétrie et d’aplatissement , qui détermine si l’asymétrie et l’aplatissement d’une variable sont cohérents ou non avec la distribution normale.

L’hypothèse nulle pour ce test est que la variable est normalement distribuée. Si la valeur p du test est inférieure à un certain niveau de signification, nous pouvons alors rejeter l’hypothèse nulle et conclure qu’il existe suffisamment de preuves pour affirmer que la variable n’est pas distribuée normalement.

*Ce test nécessite un minimum de 8 observations pour être utilisé.

Nous pouvons utiliser la commande sktest pour effectuer un test d’asymétrie et d’aplatissement sur la cylindrée variable :

déplacement du test

Voici comment interpréter le résultat du test :

Obs : 74. C’est le nombre d’observations utilisées dans le test.

adj chi(2) : 5,81. Il s’agit de la statistique du test du chi carré pour le test.

Prob>chi2 : 0,0547. Il s’agit de la valeur p associée à la statistique de test.

Puisque la valeur p n’est pas inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle du test. Nous n’avons pas suffisamment de preuves pour affirmer que les déplacements ne sont pas normalement répartis.

Semblable aux autres tests de normalité, vous pouvez effectuer le test d’asymétrie et d’aplatissement sur plusieurs variables à la fois en répertoriant plusieurs variables après la commande sktest .