Comment effectuer une régression linéaire simple dans Stata
La régression linéaire simple est une méthode que vous pouvez utiliser pour comprendre la relation entre une variable explicative, x, et une variable de réponse, y.
Ce tutoriel explique comment effectuer une régression linéaire simple dans Stata.
Exemple : régression linéaire simple dans Stata
Supposons que nous souhaitions comprendre la relation entre le poids d’une voiture et ses kilomètres par gallon. Pour explorer cette relation, nous pouvons effectuer une régression linéaire simple en utilisant le poids comme variable explicative et les miles par gallon comme variable de réponse.
Effectuez les étapes suivantes dans Stata pour effectuer une régression linéaire simple à l’aide de l’ensemble de données appelé auto , qui contient des données sur 74 voitures différentes.
Étape 1 : Chargez les données.
Chargez les données en tapant ce qui suit dans la zone de commande :
utilisez https://www.stata-press.com/data/r13/auto
Étape 2 : Obtenez un résumé des données.
Obtenez une compréhension rapide des données avec lesquelles vous travaillez en tapant ce qui suit dans la zone Commande :
résumer

Nous pouvons voir qu’il y a 12 variables différentes dans l’ensemble de données, mais les deux seules qui nous intéressent sont mpg etweight .
Étape 3 : Visualisez les données.
Avant d’effectuer une régression linéaire simple, créons d’abord un nuage de points du poids par rapport au mpg afin de pouvoir visualiser la relation entre ces deux variables et vérifier les valeurs aberrantes évidentes. Tapez ce qui suit dans la zone Commande pour créer un nuage de points :
dispersion du poids mpg
Cela produit le nuage de points suivant :
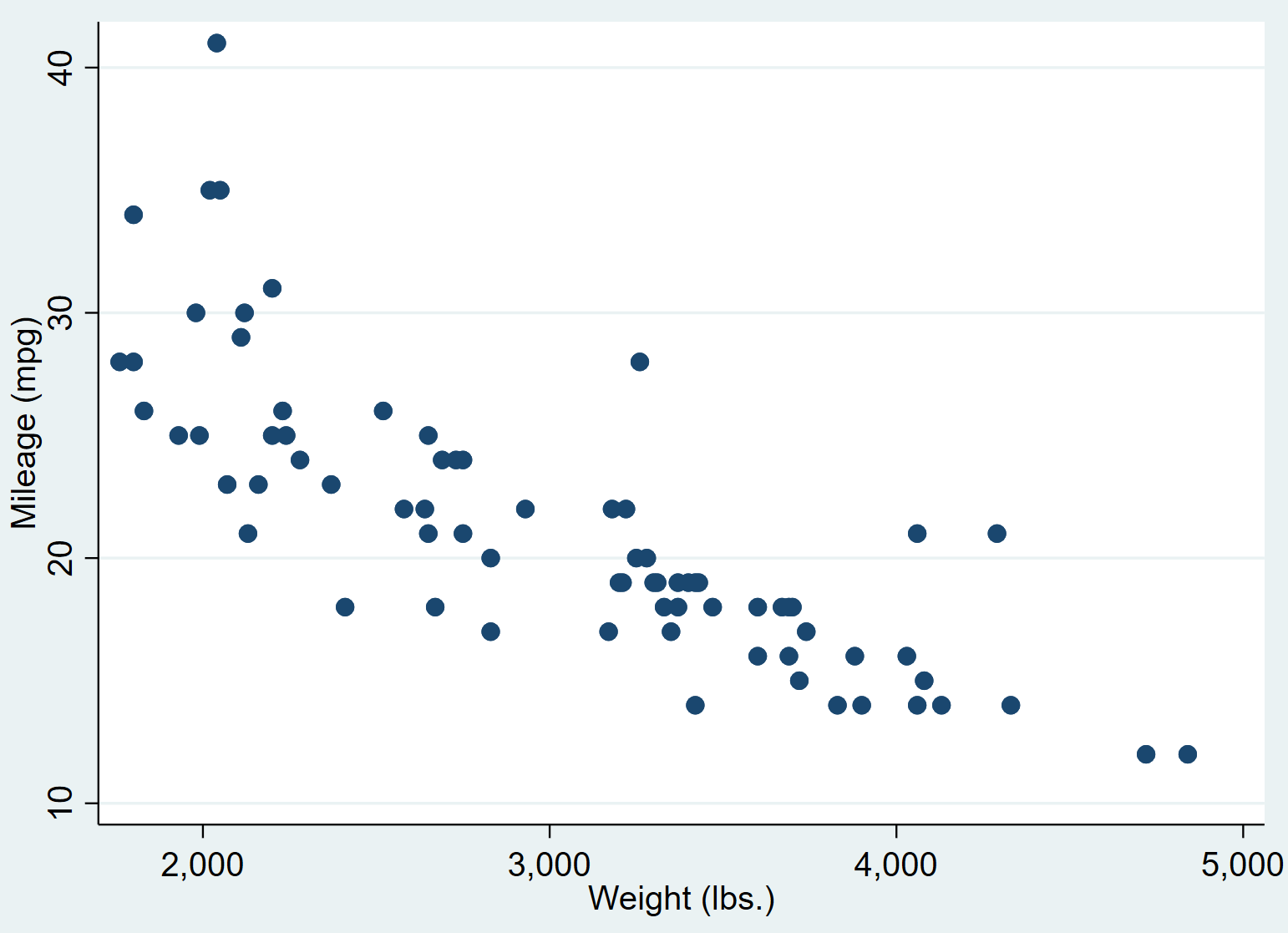
Nous pouvons voir que les voitures avec des poids plus élevés ont tendance à avoir moins de kilomètres par gallon. Pour quantifier cette relation, nous allons maintenant effectuer une simple régression linéaire.
Étape 4 : Effectuez une régression linéaire simple.
Tapez ce qui suit dans la zone Commande pour effectuer une régression linéaire simple en utilisant le poids comme variable explicative et mpg comme variable de réponse.
régresser le poids en mpg
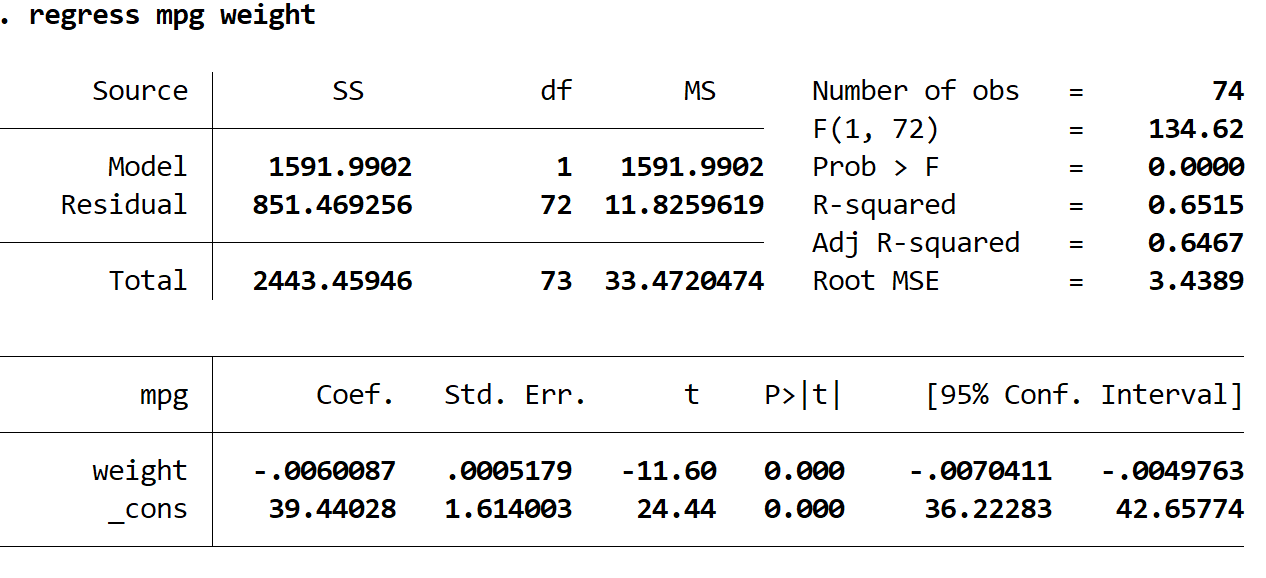
Voici comment interpréter les nombres les plus intéressants du résultat :
R au carré : 0,6515. Il s’agit de la proportion de la variance de la variable de réponse qui peut être expliquée par la variable explicative. Dans cet exemple, 65,15 % de la variation du mpg peut être expliquée par le poids.
Coef (poids) : -0,006. Cela nous indique la variation moyenne de la variable de réponse associée à une augmentation d’une unité de la variable explicative. Dans cet exemple, chaque augmentation de poids d’une livre est associée à une diminution de 0,006 mpg en moyenne.
Coef (_cons) : 39,44028. Cela nous indique la valeur moyenne de la variable de réponse lorsque la variable explicative est nulle. Dans cet exemple, le mpg moyen est de 39,44028 lorsque le poids d’une voiture est nul. Cela n’a pas vraiment de sens à interpréter puisque le poids d’une voiture ne peut pas être nul, mais le nombre 39,44028 est nécessaire pour former une équation de régression.
P>|t| (poids) : 0,000. Il s’agit de la valeur p associée à la statistique de test pour le poids. Dans ce cas, puisque cette valeur est inférieure à 0,05, nous pouvons conclure qu’il existe une relation statistiquement significative entre le poids et le mpg.
Équation de régression : Enfin, nous pouvons former une équation de régression en utilisant les deux valeurs de coefficient. Dans ce cas, l’équation serait :
mpg prédit = 39,44028 – 0,0060087*(poids)
Nous pouvons utiliser cette équation pour trouver le mpg prévu pour une voiture, compte tenu de son poids. Par exemple, une voiture qui pèse 4 000 livres devrait avoir un mpg de 15,405 :
mpg prédit = 39,44028 – 0,0060087*(4000) = 15,405
Étape 5 : Rapportez les résultats.
Enfin, nous souhaitons rapporter les résultats de notre régression linéaire simple. Voici un exemple de la façon de procéder :
Une régression linéaire a été réalisée pour quantifier la relation entre le poids d’une voiture et ses miles par gallon. Un échantillon de 74 voitures a été utilisé dans l’analyse.
Les résultats ont montré qu’il existait une relation statistiquement significative entre le poids et le mpg (t = -11,60, p < 0,0001) et que le poids représentait 65,15 % de la variabilité expliquée du mpg.
L’équation de régression s’est avérée être :
mpg prédit = 39,44 – 0,006 (poids)
Chaque livre supplémentaire était associée à une diminution, en moyenne, de -0,006 mille par gallon.
