Comment créer une matrice de corrélation dans Stata

En statistiques, nous cherchons souvent à comprendre la relation entre deux variables. Par exemple, nous pourrions vouloir comprendre la relation entre le nombre d’heures d’études d’un étudiant et la note qu’il obtient à l’examen.

Une façon de quantifier cette relation consiste à utiliser le coefficient de corrélation de Pearson , qui est une mesure de l’association linéaire entre deux variables . Il a une valeur comprise entre -1 et 1 où :

• -1 indique une corrélation linéaire parfaitement négative entre deux variables
• 0 indique aucune corrélation linéaire entre deux variables
• 1 indique une corrélation linéaire parfaitement positive entre deux variables

Plus le coefficient de corrélation s’éloigne de zéro, plus la relation entre les deux variables est forte.

Mais dans certains cas, nous souhaitons comprendre la corrélation entre plusieurs paires de variables. Dans ces cas, nous pouvons créer une matrice de corrélation , qui est un tableau carré qui montre les coefficients de corrélation entre plusieurs combinaisons de variables par paires.

Dans ce tutoriel, nous expliquons comment créer une matrice de corrélation dans Stata.

Comment créer une matrice de corrélation dans Stata

La commande corr peut être utilisée pour produire une matrice de corrélation pour un ensemble de données particulier dans Stata.

Pour illustrer cela, chargeons les données du recensement de 1980 dans Stata en tapant ce qui suit dans la zone de commande :

utilisez https://www.stata-press.com/data/r13/census13

Nous pouvons ensuite obtenir un résumé rapide de l’ensemble de données en tapant ce qui suit dans la zone de commande :

résumer

Cela produit le tableau suivant :

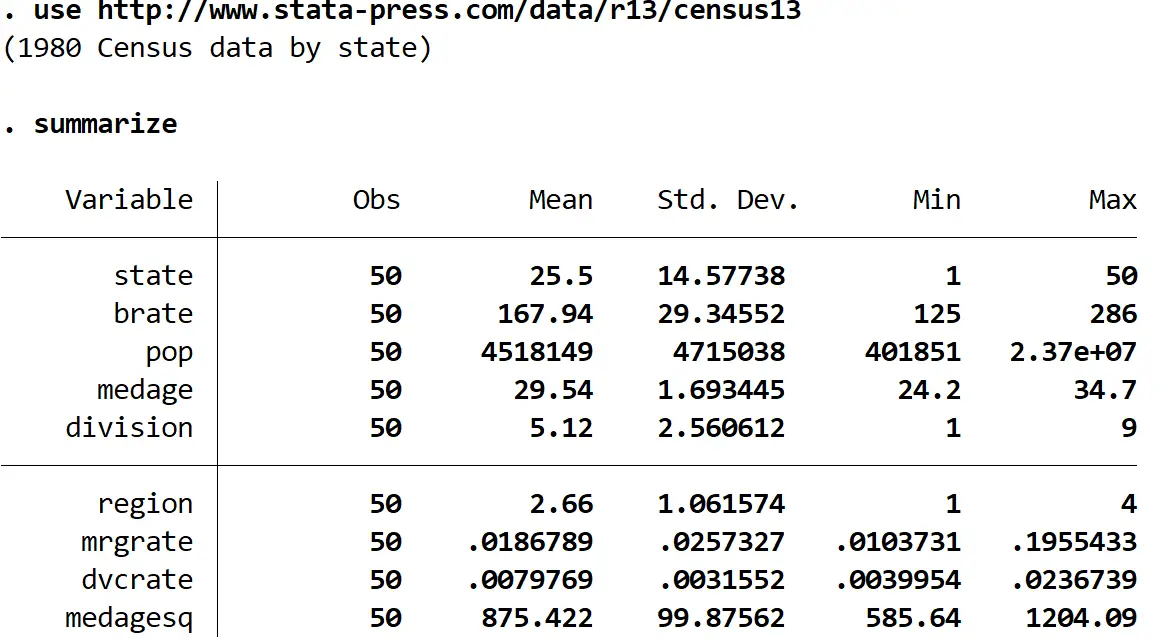
Nous voyons que l’ensemble de données contient neuf variables différentes. Pour créer une matrice de corrélation pour chaque combinaison par paire de variables de l’ensemble de données, nous pouvons saisir ce qui suit dans la zone de commande :

corr

Cela produit la matrice de corrélation suivante :

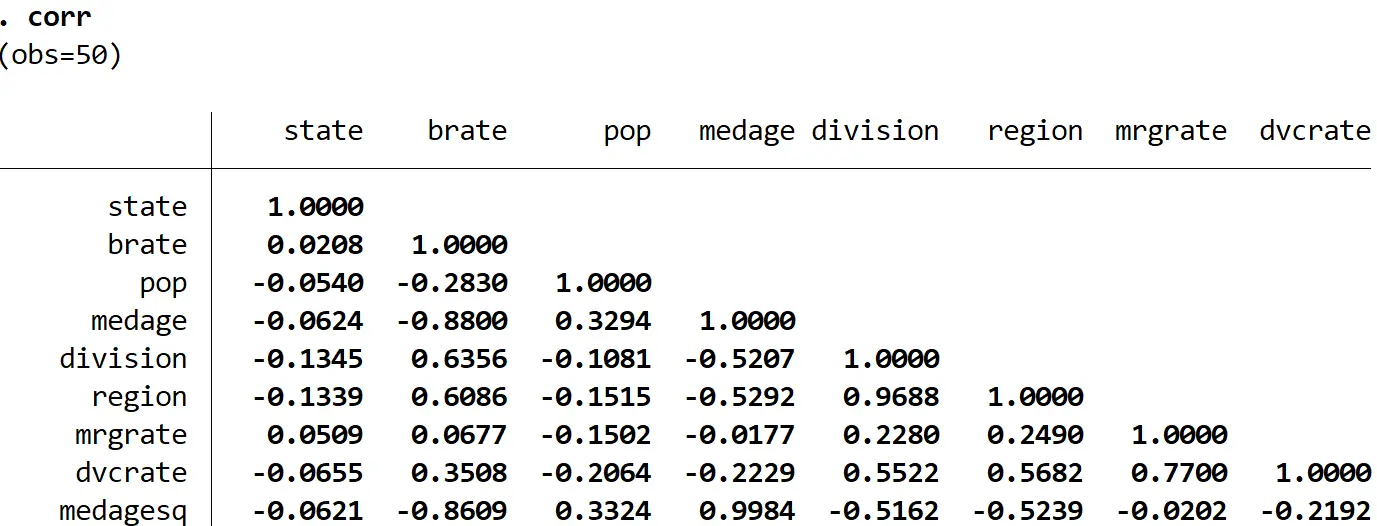
Les nombres indiqués dans le tableau représentent les coefficients de corrélation de Pearson pour chaque combinaison de variables par paire. Par exemple, la corrélation entre la population et l’État est de -0,0540 . Cela indique que ces deux variables sont légèrement corrélées négativement.

Notez que les corrélations le long des diagonales du tableau sont chacune de 1,0000, puisque chaque variable est parfaitement corrélée avec elle-même.

Vous pouvez également créer une matrice de corrélation uniquement pour un certain sous-ensemble de variables dans un ensemble de données en spécifiant les variables après la commande corr . Par exemple, voici comment créer une matrice de corrélation uniquement pour les variables pop , medage et region :

corr pop medage région

Cela produit la matrice de corrélation suivante pour ces trois variables uniquement :

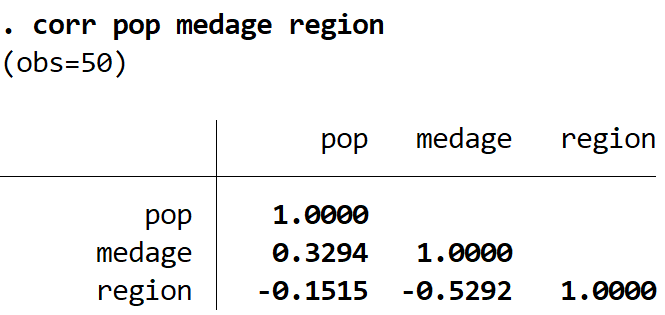
Il est également possible de placer une étoile à côté des coefficients de corrélation statistiquement significatifs à un certain niveau de signification en utilisant la commande pwcorr (qui produit le même résultat que corr ) avec la commande star() .

Par exemple, le code suivant produit une matrice de corrélation pour chaque variable de l’ensemble de données du recensement et place une étoile à côté des coefficients de corrélation qui sont statistiquement significatifs à α = 0,05 :

pwcorr, étoile (.05)

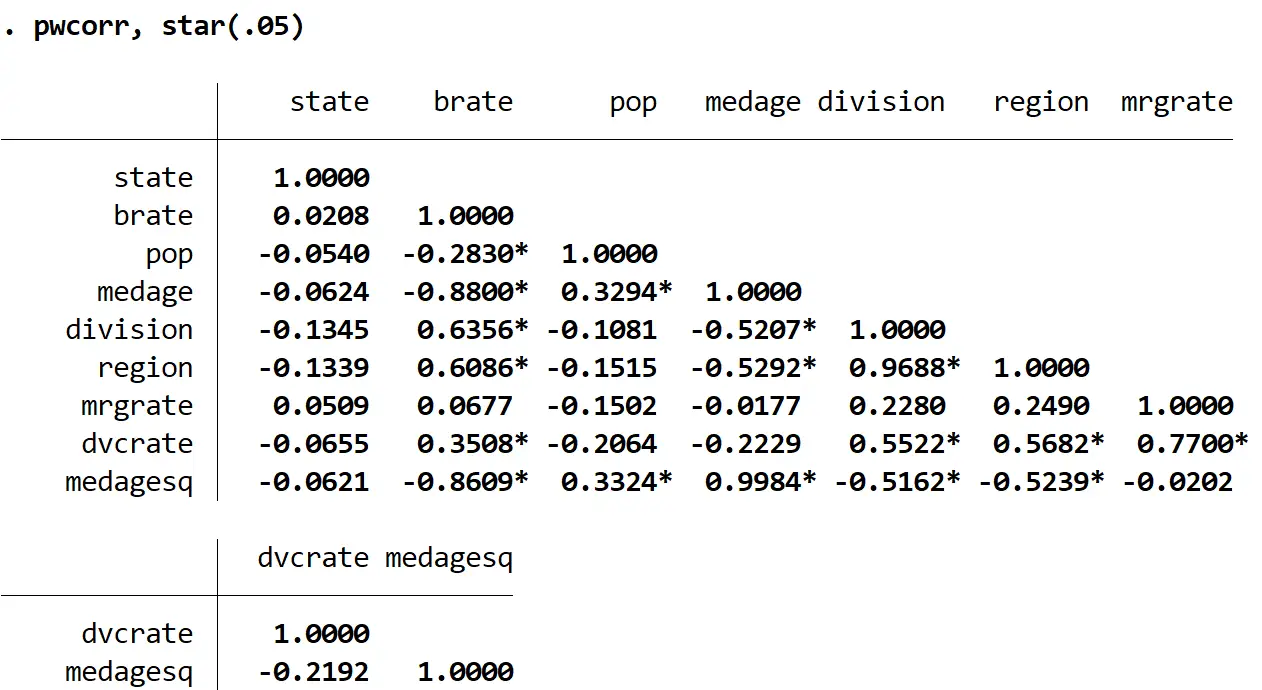
Remarquez combien plusieurs des coefficients de corrélation du tableau sont statistiquement significatifs à α = 0,05. Nous pourrions définir α sur n’importe quel nombre que nous souhaitons, mais les choix courants sont 0,01, 0,05 et 0,10.

En général, plus la valeur de α est basse, moins les coefficients de corrélation seront statistiquement significatifs. Par exemple, supposons que nous définissons α = 0,01.

pwcorr, étoile (.01)

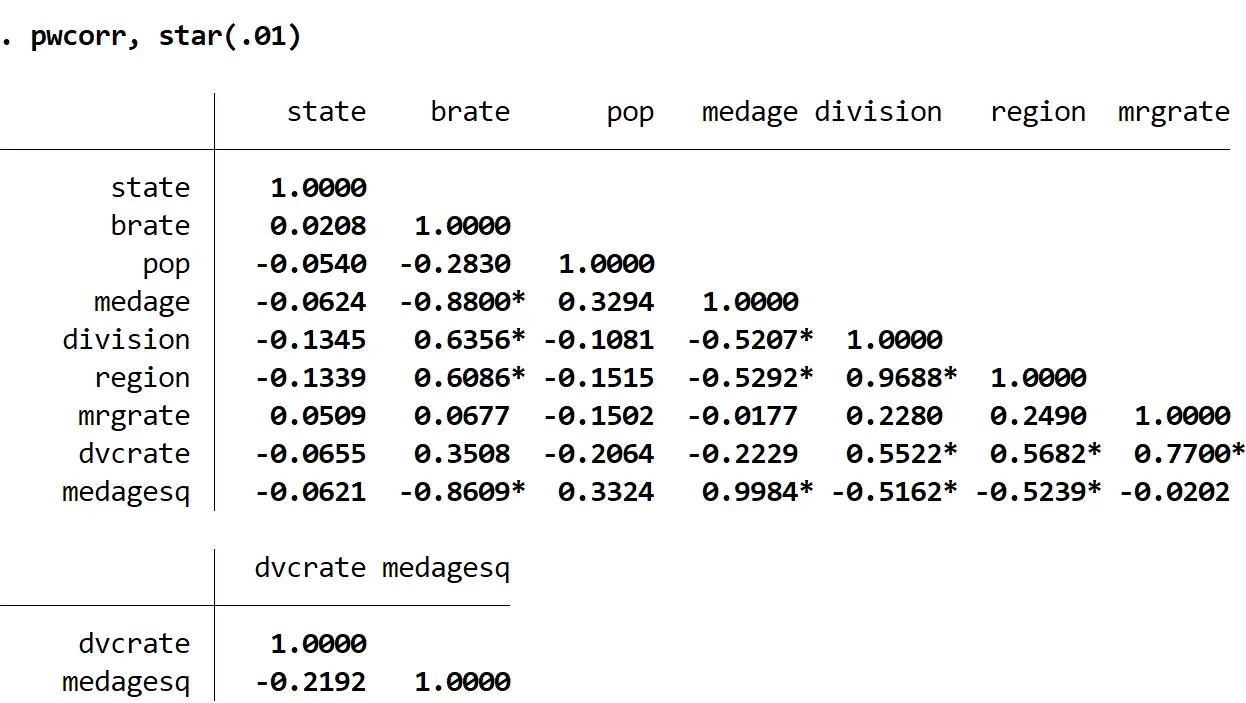
Remarquez combien moins de coefficients de corrélation ont une étoile à côté d’eux.