Comment interpréter les rapports de cotes
En statistiques, la probabilité fait référence aux chances qu’un événement se produise. Il est calculé comme suit :
PROBABILITÉ:
P(événement) = (# résultats souhaitables) / (# résultats possibles)
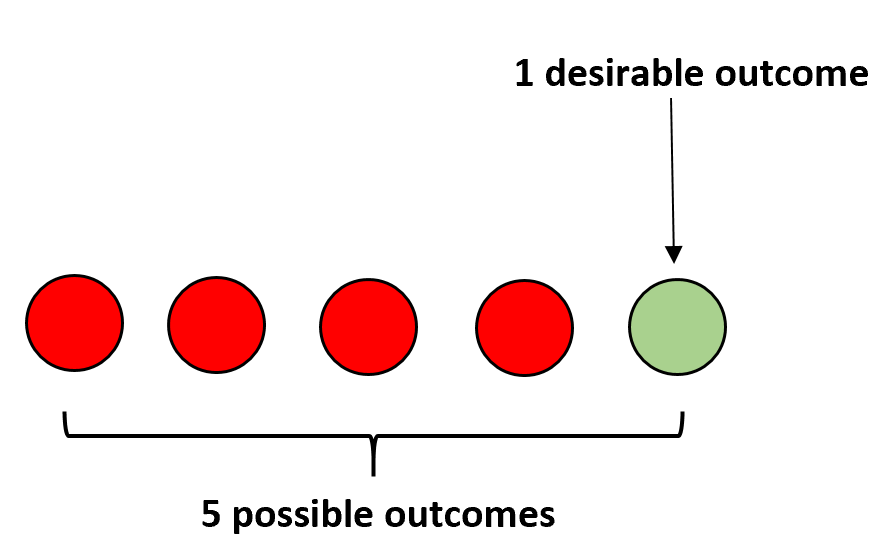
Par exemple, supposons que nous ayons quatre boules rouges et une boule verte dans un sac. Si vous fermez les yeux et sélectionnez une balle au hasard, la probabilité que vous choisissiez une balle verte est calculée comme suit :
P(vert) = 1 / 5 = 0,2 .
Les chances qu’un événement se produise peuvent être calculées comme suit :
CHANCES:
Chances (événement) = P (événement se produit) / 1-P (événement se produit)
Par exemple, les chances de tirer une balle verte sont (0,2) / 1-(0,2) = 0,2 / 0,8 = 0,25 .
L’ odds ratio est le rapport de deux probabilités.
RAPPORT DE CHANCE :
Rapport de cotes = Chances de l’événement A / Chances de l’événement B
Par exemple, nous pourrions calculer le rapport de cotes entre le choix d’une balle rouge et d’une balle verte.
La probabilité de tirer une boule rouge est de 4/5 = 0,8 .
Les chances de tirer une boule rouge sont (0,8) / 1-(0,8) = 0,8 / 0,2 = 4 .
Le rapport de cotes pour choisir une boule rouge par rapport à une boule verte est calculé comme suit :
Cotes (rouge) / Cotes (vert) = 4 / 0,25 = 16 .
Ainsi, les chances de tirer une balle rouge sont 16 fois plus grandes que les chances de tirer une balle verte.
Quand les rapports de cotes sont-ils utilisés dans le monde réel ?
Dans le monde réel, les rapports de cotes sont utilisés dans divers contextes dans lesquels les chercheurs souhaitent comparer les probabilités que deux événements se produisent. Voici quelques exemples.
Exemple n°1 : Interprétation des rapports de cotes
Les chercheurs veulent savoir si un nouveau traitement améliore les chances qu’un patient connaisse un résultat positif en matière de santé par rapport à un traitement existant. Le tableau suivant montre le nombre de patients qui ont connu un résultat de santé positif ou négatif, en fonction du traitement.

Les chances qu’un patient connaisse un résultat positif avec le nouveau traitement peuvent être calculées comme suit :
Chances = P(positif) / 1 – P(positif) = (50/90) / 1-(50/90) = (50/90) / (40/90) = 1,25
Les chances qu’un patient connaisse un résultat positif avec le traitement existant peuvent être calculées comme suit :
Chances = P(positif) / 1 – P(positif) = (42/90) / 1-(42/90) = (42/90) / (48/90) = 0,875
Ainsi, le rapport de cotes d’obtenir un résultat positif avec le nouveau traitement par rapport au traitement existant peut être calculé comme suit :
Rapport de cotes = 1,25 / 0,875 = 1,428 .
Nous interprétons cela comme signifiant que les chances qu’un patient obtienne un résultat positif en utilisant le nouveau traitement sont 1,428 fois les chances qu’un patient obtienne un résultat positif en utilisant le traitement existant.
En d’autres termes, les chances de connaître un résultat positif sont augmentées de 42,8 % avec le nouveau traitement.
Exemple n°2 : Interprétation des rapports de cotes
Les spécialistes du marketing veulent savoir si une publicité incite les clients à acheter un article donné plus souvent qu’une autre publicité. Ils diffusent donc chaque publicité à 100 personnes. Le tableau suivant indique le nombre de personnes qui ont acheté l’article, en fonction de la publicité qu’elles ont vue :
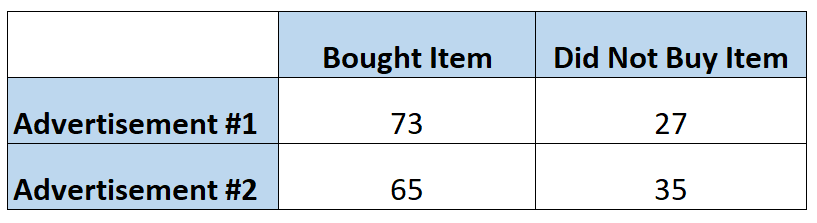
Les chances qu’un individu achète l’article après avoir vu la première publicité peuvent être calculées comme suit :
Cotes = P(acheté) / 1 – P(acheté) = (73/100) / 1-(73/100) = (73/100) / (27/100) = 2,704
Les chances qu’un individu achète l’article après avoir vu la deuxième publicité peuvent être calculées comme suit :
Cotes = P(acheté) / 1 – P(acheté) = (65/100) / 1-(65/10) = (65/100) / (35/100) = 1,857
Ainsi, le rapport de cotes pour un client qui achète l’article après avoir vu la première publicité par rapport à l’achat après avoir vu la deuxième publicité peut être calculé comme suit :
Rapport de cotes = 2,704 / 1,857 = 1,456 .
Nous interprétons cela comme signifiant que les chances qu’un individu achète l’article après avoir vu la première publicité sont 1,456 fois les chances qu’un individu achète l’article après avoir vu la deuxième publicité.
En d’autres termes, les chances d’acheter l’article sont augmentées de 45,6 % grâce à la première annonce.
Ressources additionnelles
Comment calculer le rapport de cotes et le risque relatif dans Excel
Comment interpréter un rapport de cotes inférieur à 1
Comment interpréter le risque relatif
