Une explication simple de la correction de continuité dans les statistiques
Une correction de continuité est appliquée lorsque vous souhaitez utiliser une distribution continue pour approximer une distribution discrète. Généralement, il est utilisé lorsque vous souhaitez utiliser une distribution normale pour approximer une distribution binomiale .
Rappelons que la distribution binomiale nous indique la probabilité d’obtenir x succès dans n essais, étant donné que la probabilité de succès dans un seul essai est p . Pour répondre aux questions sur la probabilité avec une distribution binomiale, nous pourrions simplement utiliser un calculateur de distribution binomiale , mais nous pourrions également approximer la probabilité en utilisant une distribution normale avec une correction de continuité.
Une correction de continuité est le nom donné à l’ajout ou à la soustraction de 0,5 à une valeur x discrète .
Par exemple, supposons que nous souhaitions trouver la probabilité qu’une pièce tombe sur face inférieure ou égale à 45 fois au cours de 100 lancers. Autrement dit, nous voulons trouver P(X ≤ 45). Pour utiliser la distribution normale pour approximer la distribution binomiale, nous trouverions plutôt P(X ≤ 45,5).
Le tableau suivant indique quand vous devez ajouter ou soustraire 0,5, en fonction du type de probabilité que vous essayez de trouver :
| Utiliser la distribution binomiale | Utilisation de la distribution normale avec correction de continuité |
|---|---|
| X = 45 | 44,5 < X < 45,5 |
| X ≤ 45 | X < 45,5 |
| X < 45 | X < 44,5 |
| X ≥ 45 | X > 44,5 |
| X > 45 | X > 45,5 |
Note:
Il est uniquement approprié d’appliquer une correction de continuité à la distribution normale pour se rapprocher de la distribution binomiale lorsque n*p et n*(1-p) valent tous deux au moins 5.
Par exemple, supposons que n = 15 et p = 0,6. Dans ce cas:
n*p = 15 * 0,6 = 9
n*(1-p) = 15 * (1 – 0,6) = 15 * (0,4) = 6
Puisque ces deux nombres sont supérieurs ou égaux à 5, il serait acceptable d’appliquer une correction de continuité dans ce scénario.
L’exemple suivant illustre comment appliquer une correction de continuité à la distribution normale pour se rapprocher de la distribution binomiale.
Exemple d’application d’une correction de continuité
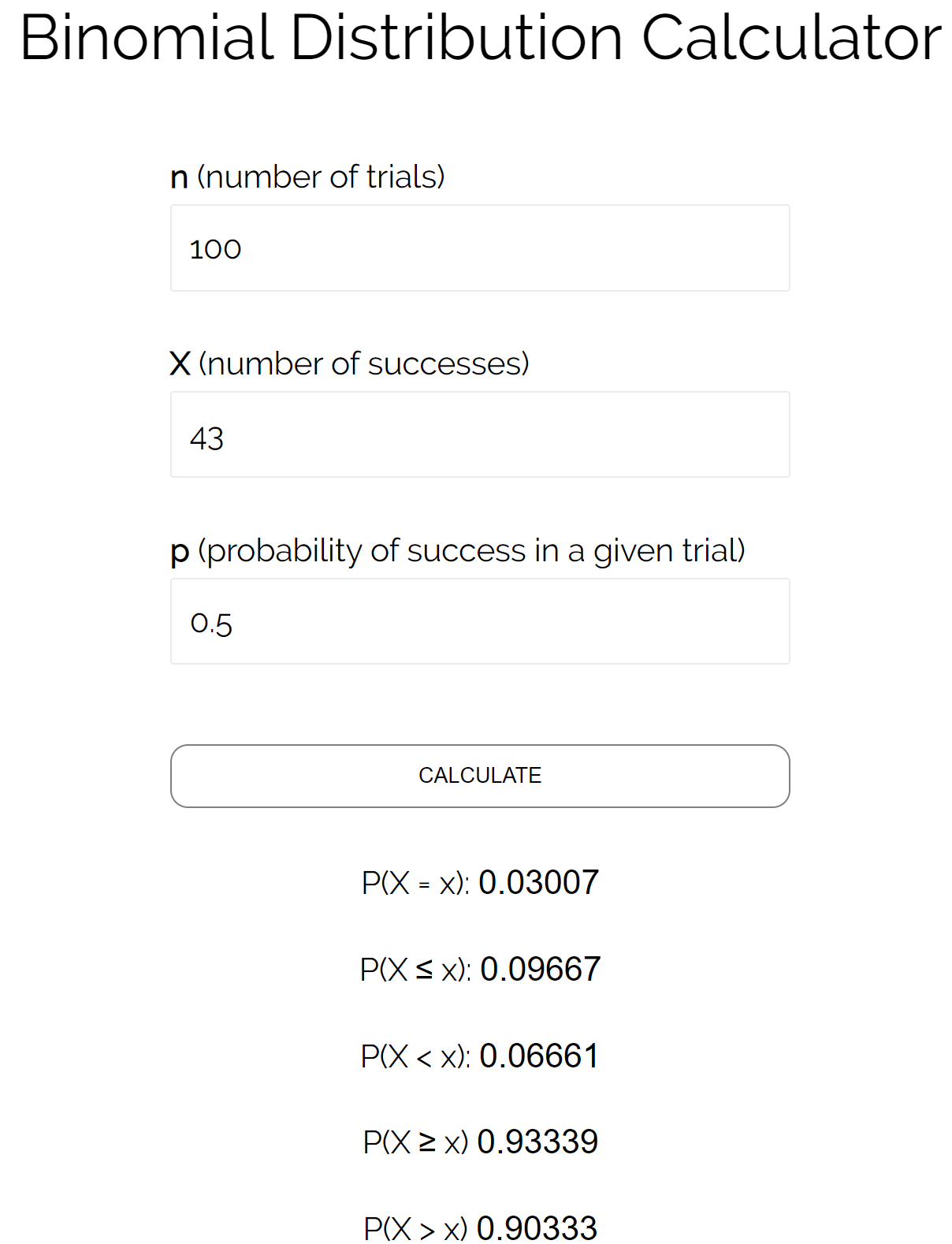
Supposons que nous voulions connaître la probabilité qu’une pièce tombe sur face inférieure ou égale à 43 fois au cours de 100 lancers. Dans ce cas:
n = nombre d’essais = 100
X = nombre de réussites = 43
p = probabilité de succès dans un essai donné = 0,50
Nous pouvons insérer ces nombres dans le calculateur de distribution binomiale pour voir que la probabilité que la pièce atterrisse sur face inférieure ou égale à 43 fois est de 0,09667 .
Pour approximer la distribution binomiale en appliquant une correction de continuité à la distribution normale, nous pouvons utiliser les étapes suivantes :
Étape 1 : Vérifiez que n*p et n*(1-p) sont tous deux au moins 5 .
n*p = 100*0,5 = 50
n*(1-p) = 100*(1 – 0,5) = 100*0,5 = 50
Les deux nombres sont supérieurs ou égaux à 5, nous pouvons donc continuer.
Étape 2 : Déterminez si vous devez ajouter ou soustraire 0,5
En nous référant au tableau ci-dessus, nous voyons que nous sommes censés ajouter 0,5 lorsque nous travaillons avec une probabilité sous la forme de X ≤ 43. Ainsi, nous trouverons P(X< 43,5).
Étape 3 : Trouvez la moyenne (μ) et l’écart type (σ) de la distribution binomiale.
µ = n*p = 100*0,5 = 50
σ = √ n*p*(1-p) = √ 100*.5*(1-.5) = √ 25 = 5
Étape 4 : Trouvez le score z en utilisant la moyenne et l’écart type trouvés à l’étape précédente.
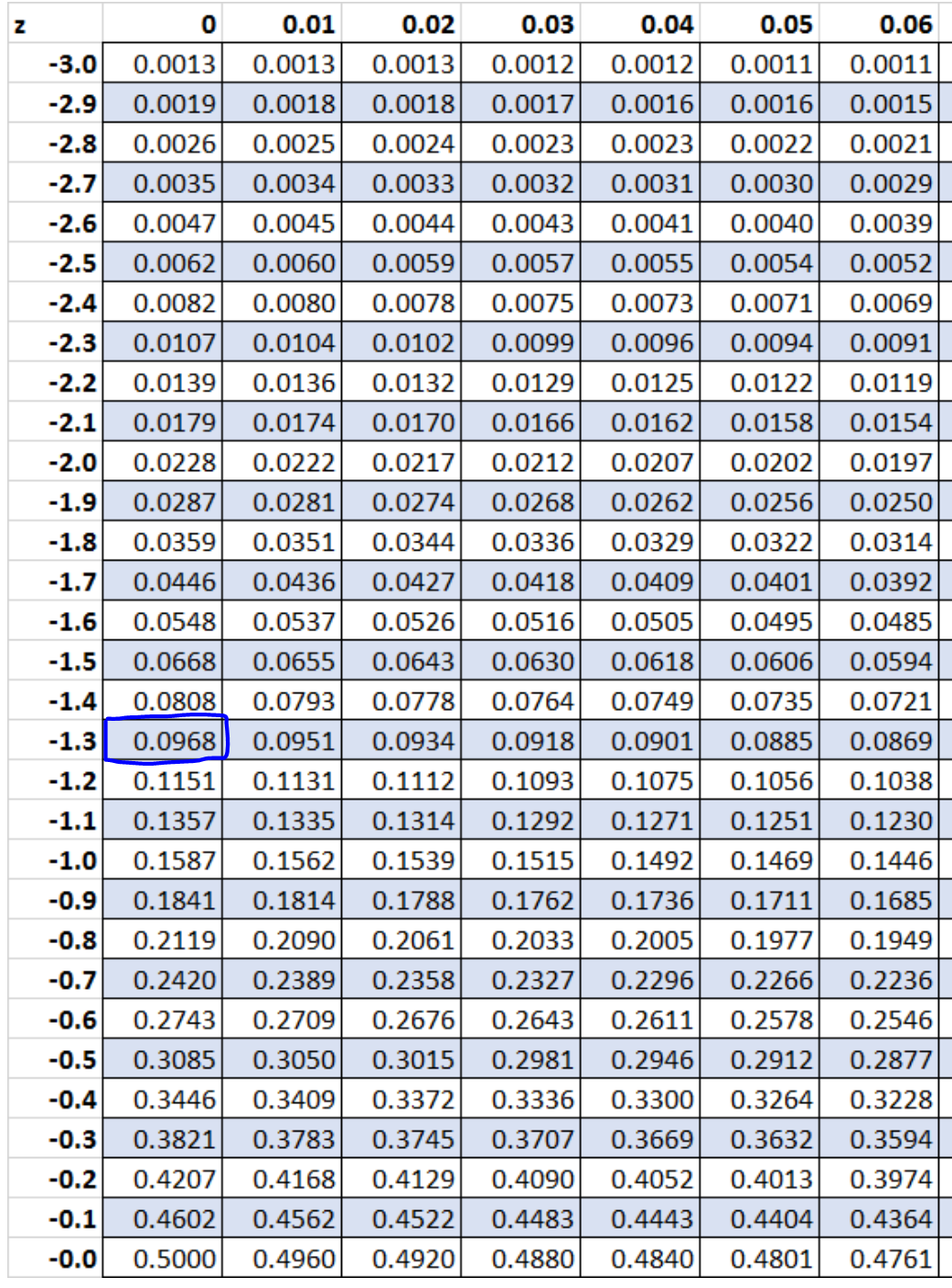
z = (x – μ) / σ = (43,5 – 50) / 5 = -6,5 / 5 = -1,3.
Étape 5 : Utilisez le tableau Z pour trouver la probabilité associée au score z.
D’après le tableau Z, la probabilité associée à z = -1,3 est 0,0968 .
Ainsi, la probabilité exacte que nous avons trouvée en utilisant la distribution binomiale était de 0,09667 tandis que la probabilité approximative que nous avons trouvée en utilisant la correction de continuité avec la distribution normale était de 0,0968 . Ces deux valeurs sont assez proches.
Quand utiliser une correction de continuité
Avant que les logiciels statistiques modernes n’existent et que les calculs devaient être effectués manuellement, les corrections de continuité étaient souvent utilisées pour trouver des probabilités impliquant des distributions discrètes. Aujourd’hui, les corrections de continuité jouent moins de rôle dans le calcul des probabilités puisque nous pouvons généralement compter sur des logiciels ou des calculatrices pour calculer les probabilités à notre place.
Au lieu de cela, il s’agit simplement d’un sujet abordé dans les cours de statistiques pour illustrer la relation entre une distribution binomiale et une distribution normale et pour montrer qu’il est possible pour une distribution normale de se rapprocher d’une distribution binomiale en appliquant une correction de continuité.
Calculateur de correction de continuité
Utilisez le calculateur de correction de continuité pour appliquer automatiquement une correction de continuité à une distribution normale afin d’approcher les probabilités binomiales.
