Kendall’s Tau : définition + exemple
En statistique, la corrélation fait référence à la force et à la direction d’une relation entre deux variables. La valeur d’un coefficient de corrélation peut aller de -1 à 1, -1 indiquant une relation négative parfaite, 0 indiquant l’absence de relation et 1 indiquant une relation positive parfaite.
Le coefficient de corrélation le plus couramment utilisé est le coefficient de corrélation de Pearson , qui mesure l’association linéaire entre deux variables numériques.
Un coefficient de corrélation moins couramment utilisé est le Tau de Kendall , qui mesure la relation entre deux colonnes de données classées.
La formule pour calculer le Tau de Kendall, souvent abrégé τ, est la suivante :
τ = (CD) / (C+D)
où:
C = le nombre de paires concordantes
D = le nombre de paires discordantes
L’exemple suivant illustre comment utiliser cette formule pour calculer le coefficient de corrélation de rang Tau de Kendall pour deux colonnes de données classées.
Exemple de calcul du Tau de Kendall
Supposons que deux entraîneurs de basket-ball classent 12 de leurs joueurs du pire au meilleur. Le tableau suivant montre les classements que chaque entraîneur a attribué aux joueurs :
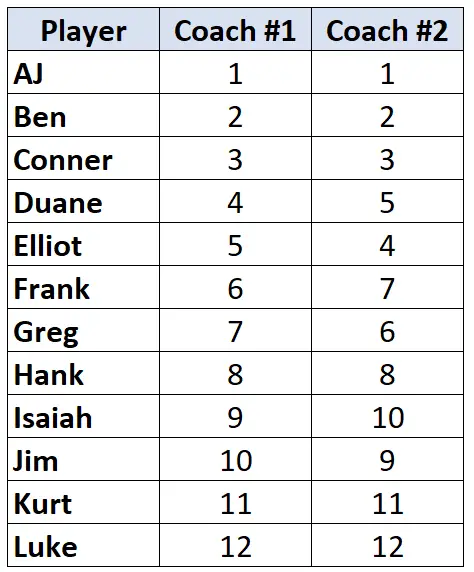
Étant donné que nous travaillons avec deux colonnes de données classées, il est approprié d’utiliser le Tau de Kendall pour calculer la corrélation entre les classements des deux entraîneurs. Suivez les étapes suivantes pour calculer le Tau de Kendall :
Étape 1 : Comptez le nombre de paires concordantes.
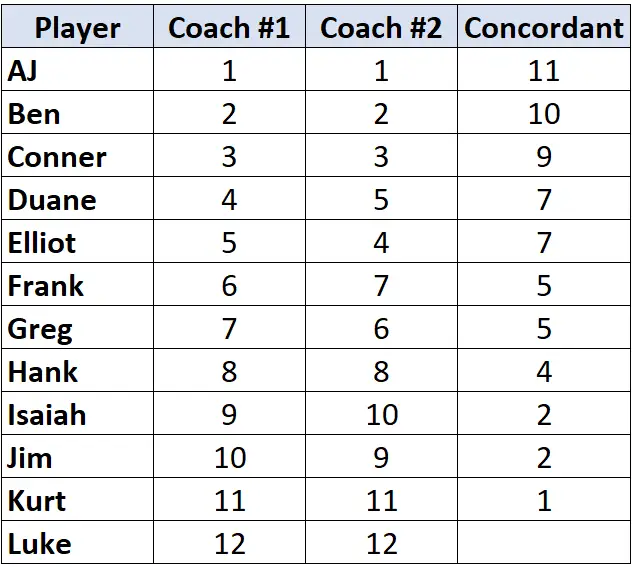
Regardez uniquement les classements de l’entraîneur n°2. En commençant par le premier joueur, comptez combien de rangs en dessous de lui sont plus grands . Par exemple, il y a 11 nombres en dessous de « 1 » qui sont plus grands, nous écrirons donc 11 :
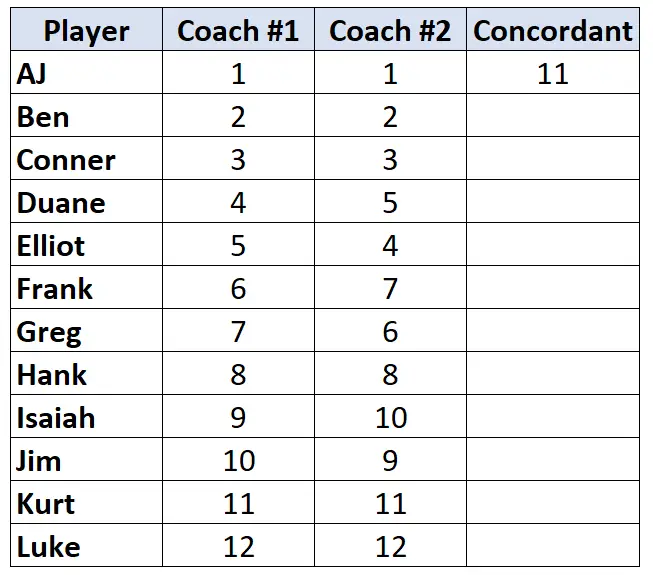
Passez au joueur suivant et répétez le processus. Il y a 10 nombres en dessous de « 2 » qui sont plus grands, nous écrirons donc 10 :
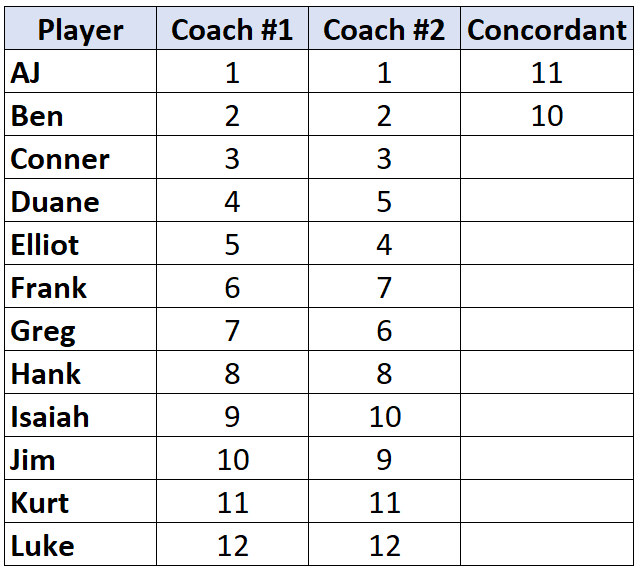
Une fois qu’on atteint un joueur dont le rang est inférieur à celui du joueur qui le précède, on lui attribue simplement la même valeur que le joueur qui le précède. Par exemple, Elliot a un rang de « 4 » qui est inférieur au rang de « 5 » du joueur précédent donc on lui attribue simplement la même valeur que le joueur qui l’a précédé :
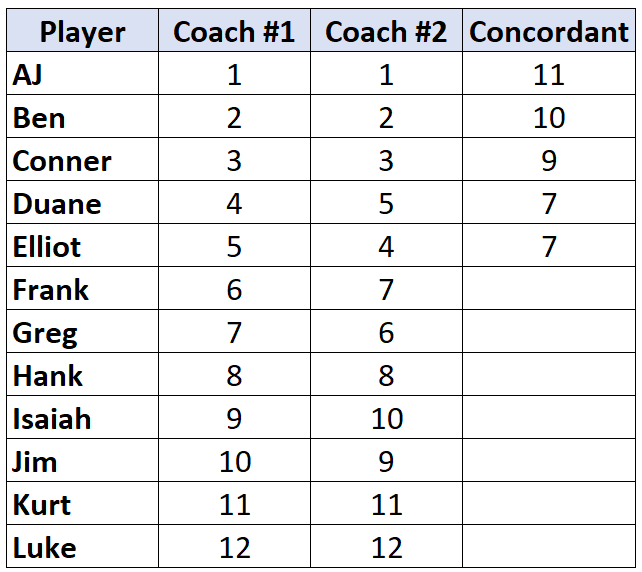
Répétez ce processus pour tous les joueurs :
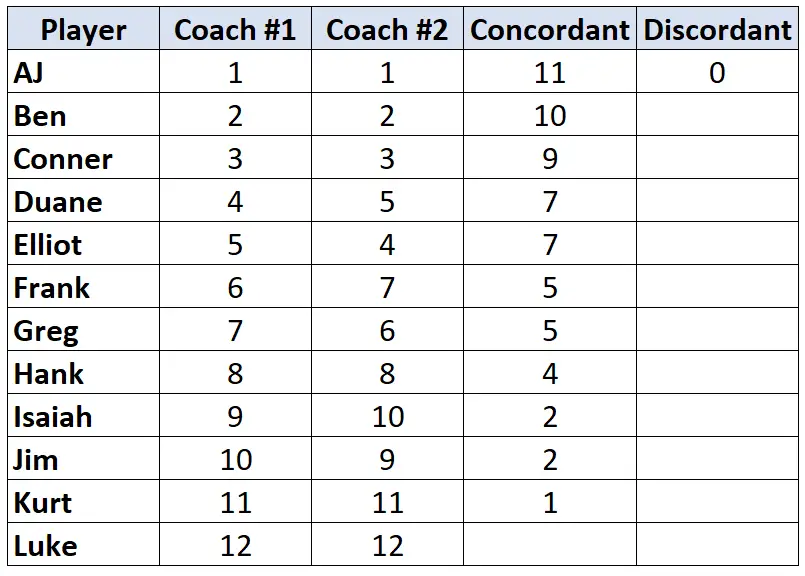
Étape 2 : Comptez le nombre de paires discordantes.
Encore une fois, regardez uniquement les classements de l’entraîneur n°2. Pour chaque joueur, comptez combien de rangs en dessous de lui sont plus petits . Par exemple, l’entraîneur n°2 a attribué à AJ le rang « 1 » et aucun joueur en dessous de lui n’a un rang inférieur. Ainsi, on lui attribue une valeur de 0 :
Répétez ce processus pour chaque joueur :
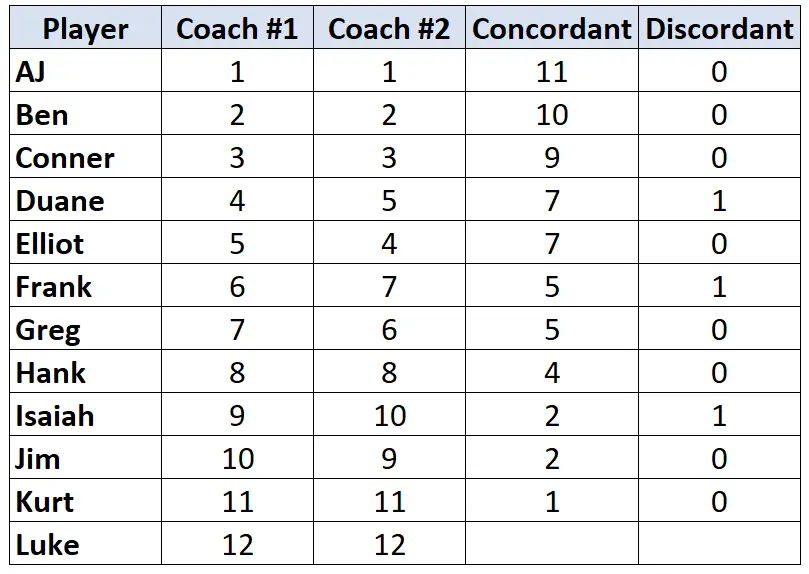
Étape 3 : Calculez la somme de chaque colonne et trouvez le Tau de Kendall.
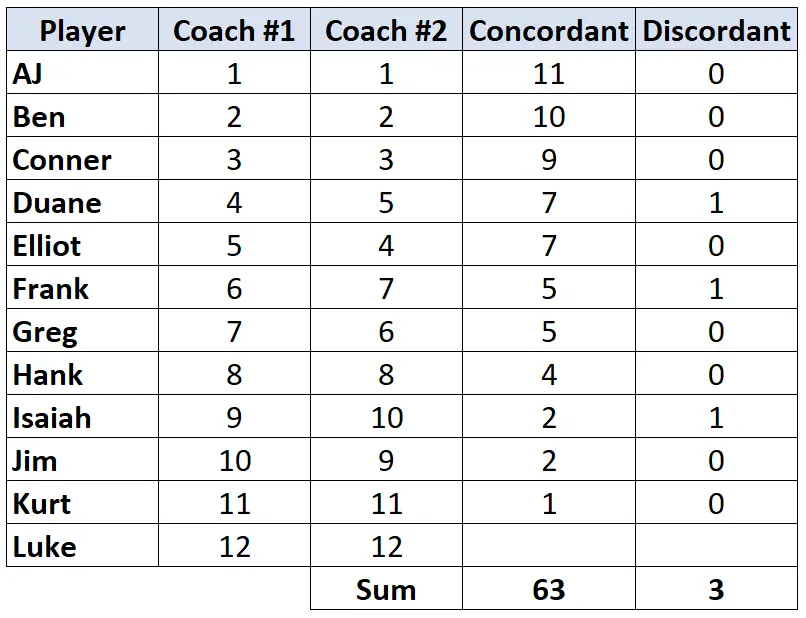
Tau de Kendall = (CD) / (C+D) = (63-3) / (63+3) = (60/66) = 0,909 .
Importance statistique du Tau de Kendall
Lorsque vous avez plus de n= 10 paires, le Tau de Kendall suit généralement une distribution normale. Vous pouvez utiliser la formule suivante pour calculer un z-score pour le Tau de Kendall :
z = 3τ*√ n(n-1) / √ 2(2n+5)
où:
τ = valeur que vous avez calculée pour le Tau de Kendall
n = nombre de paires
Voici comment calculer z pour l’exemple précédent :
z = 3(.909)*√ 12(12-1) / √ 2(2*12+5) = 4.11 .
À l’aide du calculateur de score Z à valeur P , nous voyons que la valeur p pour ce score z est de 0,00004 , ce qui est statistiquement significatif au niveau alpha de 0,05. Ainsi, il existe une corrélation statistiquement significative entre les rangs que les deux entraîneurs ont attribué aux joueurs.
Bonus : Comment calculer le Tau de Kendall dans R
Dans le logiciel de statistiques R, vous pouvez utiliser la fonction kendall.tau() de la bibliothèque VGAM pour calculer le Tau de Kendall pour deux vecteurs, qui utilise la syntaxe suivante :
kendall.tau(x, y)
où x et y sont deux vecteurs numériques d’égale longueur.
Le code suivant illustre comment calculer le Tau de Kendall pour les données exactes que nous avons utilisées dans l’exemple précédent :
#load VGAM library(VGAM) #create vector for each coach's rankings coach_1 <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12) coach_2 <- c(1, 2, 3, 5, 4, 7, 6, 8, 10, 9, 11, 12) #calculate Kendall's Tau kendall.tau(coach_1, coach_2) #[1] 0.9090909
Remarquez comment la valeur du Tau de Kendall correspond à la valeur que nous avons calculée manuellement.
