Comment effectuer un test t à deux échantillons dans Excel

Un test t à deux échantillons est utilisé pour tester si les moyennes de deux populations sont égales ou non.

Ce didacticiel explique comment effectuer un test t à deux échantillons dans Excel.

Comment effectuer un test t à deux échantillons dans Excel

Supposons que les chercheurs souhaitent savoir si deux espèces de plantes différentes dans un pays donné ont la même hauteur moyenne. Parce qu’il serait trop long de faire le tour et de mesurer chaque plante, ils décident de prélever un échantillon de 20 plantes de chaque espèce.

L’image suivante montre la hauteur (en pouces) de chaque plante dans chaque échantillon :

Nous pouvons effectuer un test t à deux échantillons pour déterminer si les deux espèces ont la même hauteur moyenne en suivant les étapes suivantes :

Étape 1 : Déterminez si les variances de la population sont égales .

Lorsque nous effectuons un test t à deux échantillons, nous devons d’abord décider si nous supposerons que les deux populations ont des variances égales ou inégales. En règle générale, nous pouvons supposer que les populations ont des variances égales si le rapport entre la plus grande variance de l’échantillon et la plus petite variance de l’échantillon est inférieur à 4 : 1.

Nous pouvons trouver la variance pour chaque échantillon à l’aide de la fonction Excel =VAR.S(Cell range) , comme le montre l’image suivante :

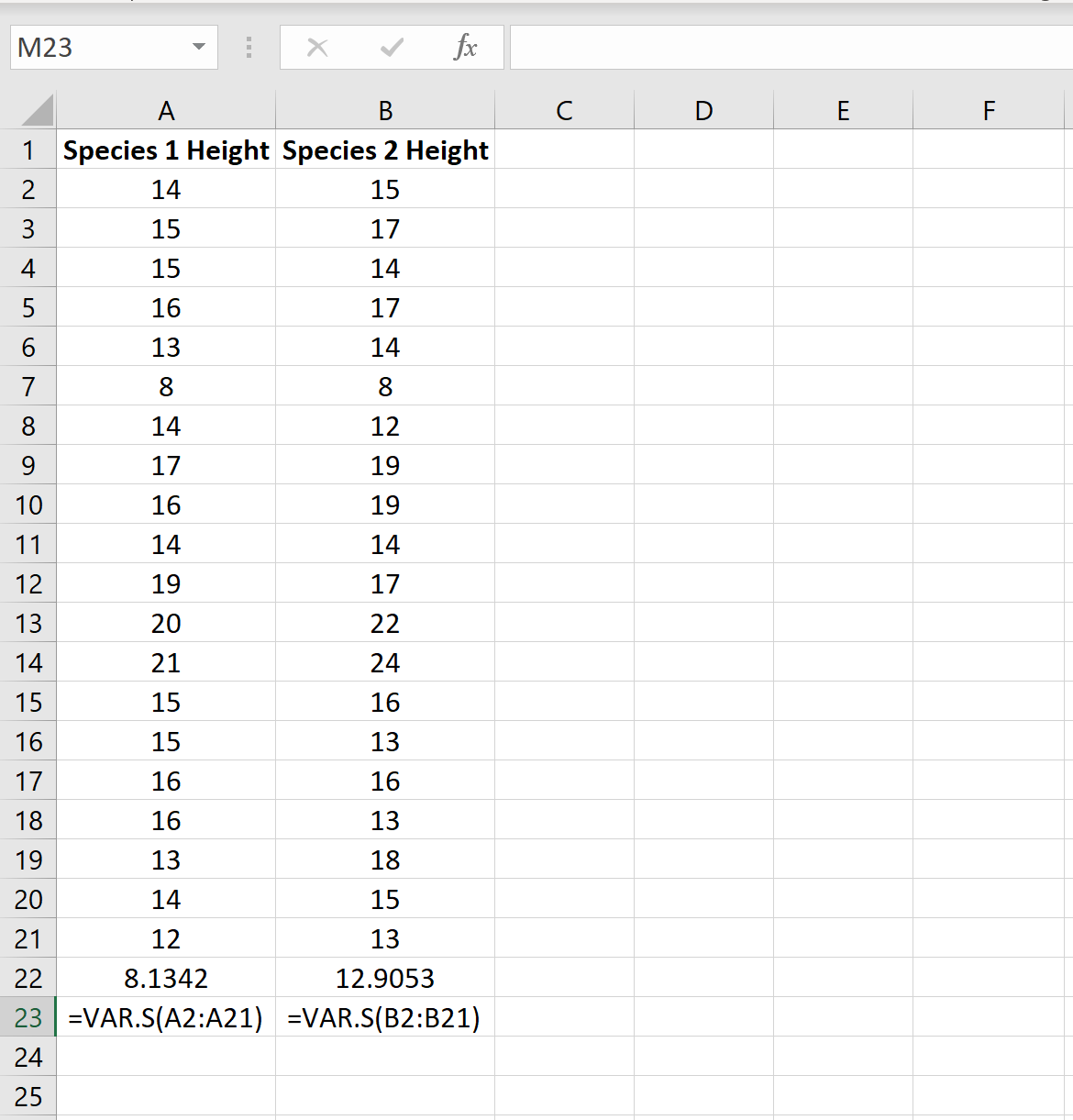
Le rapport entre la plus grande variance de l’échantillon et la plus petite variance de l’échantillon est 12,9053 / 8,1342 = 1,586 , ce qui est inférieur à 4. Cela signifie que nous pouvons supposer que les variances de la population sont égales.

Étape 2 : ouvrez le ToolPak d’analyse .

Dans l’onglet Données du ruban supérieur, cliquez sur « Analyse des données ».

Si vous ne voyez pas cette option sur laquelle cliquer, vous devez d’abord télécharger le Analysis ToolPak , qui est entièrement gratuit.

Étape 3 : Sélectionnez le test approprié à utiliser.

Sélectionnez l’option qui dit Test t : deux échantillons en supposant des variances égales , puis cliquez sur OK.

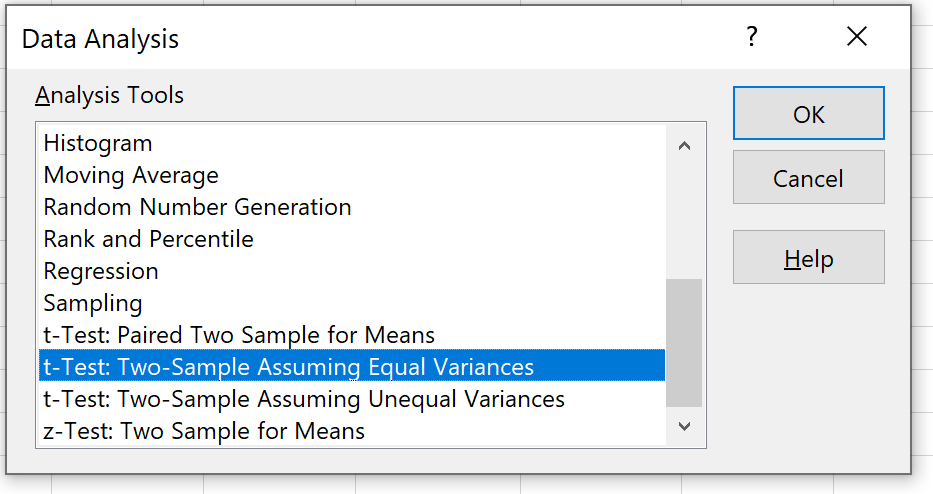
Étape 4 : Saisissez les informations nécessaires .

Entrez la plage de valeurs pour la variable 1 (notre premier échantillon), la variable 2 (notre deuxième échantillon), la différence moyenne hypothétique (dans ce cas, nous mettons « 0 » car nous voulons savoir si la véritable différence moyenne de la population est de 0), et la plage de sortie dans laquelle nous aimerions voir les résultats du test t affichés. Ensuite, cliquez sur OK.

Étape 5 : Interpréter les résultats .

Une fois que vous avez cliqué sur OK à l’étape précédente, les résultats du test t seront affichés.

Voici comment interpréter les résultats :

Moyenne : Il s’agit de la moyenne de chaque échantillon. L’échantillon 1 a une hauteur moyenne de 15,15 et l’échantillon 2 a une hauteur moyenne de 15,8 .

Variance : Il s’agit de la variance pour chaque échantillon. L’échantillon 1 a une variance de 8,13 et l’échantillon 2 a une variance de 12,90 .

Observations : Il s’agit du nombre d’observations dans chaque échantillon. Les deux échantillons contiennent 20 observations (par exemple 20 plantes individuelles dans chaque échantillon).

Variance groupée : nombre calculé en « regroupant » les variances de chaque échantillon à l’aide de la formule s ² _p = [ (n ₁ -1)s ² ₁ + (n ₂ -1)s ² ₂ ] / (n ₁ +n ₂ -2), qui s’avère être 10.51974 . Ce nombre est ensuite utilisé lors du calcul de la statistique de test t .

Différence moyenne hypothétique : le nombre sur lequel nous « émettons l’hypothèse » est la différence entre les moyennes des deux populations. Dans ce cas, nous avons choisi 0 car nous voulons tester si la différence entre les moyennes des deux populations est égale ou non à 0, par exemple s’il n’y a pas de différence.

df : Les degrés de liberté pour le test t, calculés comme n ₁ + n ₂ -2 = 20 + 20 – 2 = 38 .

t Stat : La statistique de test t , calculée comme t = [ x ₁ – x ₂ ] / √ [ s ² _p (1/n ₁ + 1/n ₂ ) ]

Dans ce cas, t = [15.15-15.8] / √ [ 10.51974(1/20+1/20) ] = -0.63374 .

P(T<=t) bilatéral : la valeur p pour un test t bilatéral. Dans ce cas, p = 0,530047 . C’est beaucoup plus grand que alpha = 0,05, nous ne parvenons donc pas à rejeter l’hypothèse nulle. Nous ne disposons pas de preuves suffisantes pour affirmer que les moyennes des deux populations sont différentes.

t Critique bilatéral : Il s’agit de la valeur critique du test, trouvée en identifiant la valeur dans le tableau de distribution t qui correspond à un test bilatéral avec alpha = 0,05 et df = 38. Cela s’avère être 2,024394 . Puisque notre statistique de test t est inférieure à cette valeur, nous ne parvenons pas à rejeter l’hypothèse nulle. Nous ne disposons pas de preuves suffisantes pour affirmer que les moyennes des deux populations sont différentes.

Notez que l’approche de la valeur p et de la valeur critique conduira toutes deux à la même conclusion.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres types de tests t dans Excel :

Comment effectuer un test t sur un échantillon dans Excel
Comment effectuer un test t pour échantillons appariés dans Excel